2.6.Применение теоремы Гаусса
Поле непрерывно распределённых зарядов
Определим теперь с помощью теоремы Остроградского-Гаусса напряжённость поля для ряда случаев.
1. Электрическое поле равномерно заряженной сферической поверхности.
Сфера
радиусом R. Пусть заряд +q равномерно
распределён по сферической поверхности
радиуса R. Распределение заряда по
поверхности характеризуется поверхностной
плотностью заряда 
(рис.4).
Поверхностной плотностью заряда называют
отношение заряда к площади поверхности,
по которой он распределён. 
.
В СИ 
.
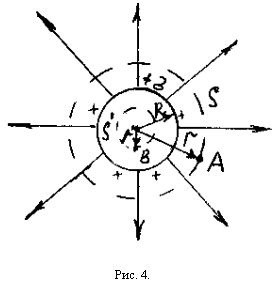
Определим напряжённость поля:
а) вне сферической поверхности, б) внутри сферической поверхности.
а)
Возьмём точку А, отстоящую от центра
заряженной сферической поверхности на
расстоянии r>R. Проведём через неё
мысленно сферическую поверхность S
радиуса r, имеющую общий центр с заряженной
сферической поверхностью. Из соображения
симметрии очевидно, что силовые линии
являются радиальными прямыми
перпендикулярными к поверхности S и
равномерно пронизывают эту поверхность,
т.е. напряжённость по всех точках этой
поверхности постоянна по величине.
Применим теорему Остроградского-Гаусса
к этой сферической поверхности S радиуса
r. Поэтому полный поток через сферу равен
N = E? S; N=E
.
С другой стороны 
.
Приравниваем: 
.
Отсюда: 
при
r>R.
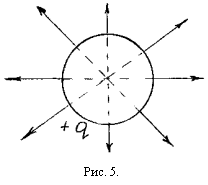
Таким образом: напряжённость, создаваемая равномерно заряженной сферической поверхностью, вне её такая же, как если бы весь заряд находился в её центре (рис.5).
б)
Найдём напряжённость поля в точках,
лежащих внутри заряженной сферической
поверхности. Возьмём точку В отстоящую
от центра сферы на расстоянии 
<R,
и проведём через эту точку сферическую
поверхность имеющую общий центр с
заряженной сферической поверхностью.
Из соображения симметрии ясно, что
напряжённость 
должна
быть численно одинакова на всей выбранной
поверхности сферы S и нормальна к ней.
Применяя теорему Остроградского-Гаусса
к сферической поверхности S на основании
формулы: N=E? S, S=4p 
т.к.
заряд внутри сферы S q = 0, то
.
Тогда 
,
E = 0 при r<R. Следовательно, напряжённость
электрического поля во всех точках
внутри равномерно заряженной сферической
поверхности равна нулю.
2. Напряжённость поля равномерно заряженной бесконечной плоскости
Рассмотрим электрическое поле создаваемое бесконечной плоскостью, заряженной с плотностью , постоянной во всех точках плоскости. По соображениям симметрии можно считать, что линии напряжённости перпендикулярны к плоскости и направлены от неё в обе стороны (рис.6).
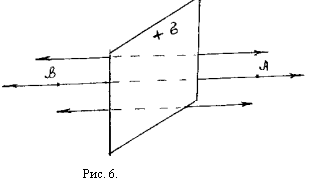
Выберем
точку А, лежащую справа от плоскости и
вычислим
в
этой точке, применяя теорему
Остроградского-Гаусса. В качестве
замкнутой поверхности выберем
цилиндрическую поверхность таким
образом, чтобы боковая поверхность
цилиндра была параллельна силовым
линиям, а его основания 
и
параллельны
плоскости и основание
проходит
через точку А (рис. 7). Рассчитаем поток
напряжённости через рассматриваемую
цилиндрическую поверхность. Поток через
боковую поверхность равен 0, т.к. линии
напряжённости параллельны боковой
поверхности. Тогда полный поток
складывается из потоков 
и 
проходящих
через основания цилиндра
и
.
Оба эти потока положительны 
=
+
;
=
;
=
;
=
=
; N
= 2
.
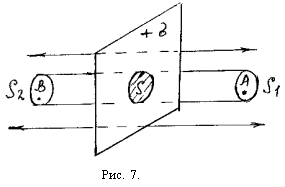
– участок плоскости лежащий внутри выбранной цилиндрической поверхности. Заряд внутри этой поверхности равен q.
.
Тогда 
; 
СГСЭ 
; 
Итак
величина
не
зависит от положения рассматриваемой
точки А и определяется только поверхностной
плоскостью зарядов 
.
Вектор
всюду
направлен перпендикулярно плоскости,
а
)
если
>0
от плоскости (рис. 8).
б) если <0 тогда к плоскости (рис. 9).
3. Поле двух параллельных плоскостей
Плоскости
заряжены разноимёнными зарядами с
плотностями +s и -s (рис.10). 
напряжённость
полей обеих плоскостей между плоскостями
направлены в одну сторону, следовательно,
их геометрическая сумма является их
арифметической суммой в вакууме 
.
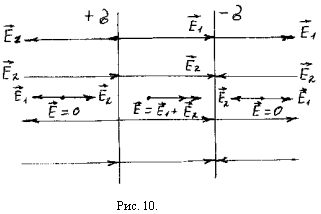
И так: во всех точках пространства между плоскостями, вектор напряжённости имеет одинаковую величину и направлен от положительно заряженной плоскости до отрицательно заряженной плоскости, т.е. поле между плоскостями однородное. Вне этих плоскостей поле равно “0” .
Пример решения задачи на вычисление электрических полей
Металлическое кольцо радиусом R имеет заряд q. Чему равны напряжённость поля и потенциал:
а) на расстоянии а от центра вдоль оси, перпендикулярной плоскости кольца; б) в центре кольца?
Решение:
Возьмём
элемент кольца 
,
который создаёт в точке А электрическое
поле напряжённостью 
(рис.11).
Вектор напряжённости 
направлен
по линии 
,
соединяющей элементы кольца
с
зарядом 
(
–
можно принять за точечный заряд) с точкой
А. Для нахождения суммарного поля надо
геометрически сложить все поля,
создаваемые каждым элементом: 
.
Вектор напряжённости
имеет
две составляющие: 
(нормальная
и касательная составляющие).
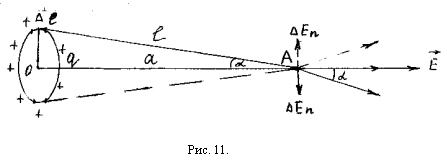
Составляющие 
от
каждых двух диаметрально расположенных
элементов взаимно уничтожаются, тогда
результирующие поле 
и
вектор направлен вдоль оси. Из рисунка
24 следует, что 
; 
где 
.
Учитывая, что напряжённость поля
точечного заряда 
получим: 
.
Для
нахождения потенциала 
суммируем
алгебраически потенциалы, создаваемые
отдельными элементами
:
В
центре кольца а = 0, поэтому из предыдущего
следует, что 
; 
.