
- •Гдава I. Элементы теории полей
- •§ 1. Алгебраические числа и минимальные многочлены
- •§ 2. Простые расширения числовых полей и их строение.
- •§ 3. Конечные расширения и их связь с простыми алгебраическими расширениями
- •§ 4. Составные расширения
- •§ 5. Составные алгебраические расширения.
- •§ 6. Простота составного алгебраического расширения.
Гдава I. Элементы теории полей
В этой главе будут
рассматриваться числовые поля, т.е.
подполя поля
![]() комплексных чисел, хотя аналогичная
теория может быть построена для любого
алгебраически замкнутого поля.
комплексных чисел, хотя аналогичная
теория может быть построена для любого
алгебраически замкнутого поля.
До сих пор изучались,
в основном, числовые поля
![]() рациональных чисел и
рациональных чисел и
![]() действительных чисел. Однако многие
задачи, в том числе задача о возможности
построения с помощью циркуля и линейки
того или иного числа, требуют рассмотрения
и других числовых полей.
действительных чисел. Однако многие
задачи, в том числе задача о возможности
построения с помощью циркуля и линейки
того или иного числа, требуют рассмотрения
и других числовых полей.
§ 1. Алгебраические числа и минимальные многочлены
Условимся, ради краткости, под полем понимать числовое поле, а под числом – комплексное число.
Определение 1.
Пусть
![]() – некоторое поле. Число
– некоторое поле. Число
![]() называется
алгебраическим относительно поля
(над полем
),
если оно является корнем некоторого
многочлена
называется
алгебраическим относительно поля
(над полем
),
если оно является корнем некоторого
многочлена
![]() .
.
Если число не является алгебраическим относительно поля , то оно называется трансцендентным относительно .
Замечание 1.
Как известно, поле
![]() является наименьшим числовым полем
(т.е. содержится в любом числовом поле).
В силу особого положения этого поля
алгебраические
и трансцендентные относительно поля
числа называются просто алгебраическими
и трансцендентными
(без добавления слов «относительно поля
»).
является наименьшим числовым полем
(т.е. содержится в любом числовом поле).
В силу особого положения этого поля
алгебраические
и трансцендентные относительно поля
числа называются просто алгебраическими
и трансцендентными
(без добавления слов «относительно поля
»).
Примеры.
Число
 есть корень многочлена
есть корень многочлена
 с рациональными коэффициентами и,
следовательно, является алгебраическим.
с рациональными коэффициентами и,
следовательно, является алгебраическим.Любое число из поля является корнем многочлена
 и, следовательно, является алгебраическим
относительно
.
и, следовательно, является алгебраическим
относительно
.Любое число является алгебраическим относительно поля . Действительно, если – вещественное число, то оно является корнем многочлена
 .
Если
– мнимое число, то оно является корнем
многочлена
.
Если
– мнимое число, то оно является корнем
многочлена
 .
.
Долгое время
считали, что все числа являются
алгебраическими. Только в 1851 г. Эрмит
обнаружил трансцендентное число
![]() ,
а в 1882 г. Линдеман доказал трансцендентность
числа
,
а в 1882 г. Линдеман доказал трансцендентность
числа
![]() .
Большой вклад в теорию трансцендентных
чисел внес советский математик А.О.
Гельфонд в 1931-36 гг. Из его результатов
в частности следует, что трансцендентными
являются числа вида
.
Большой вклад в теорию трансцендентных
чисел внес советский математик А.О.
Гельфонд в 1931-36 гг. Из его результатов
в частности следует, что трансцендентными
являются числа вида
![]() ,
где
,
где
![]() – целое,
– целое,
![]() – иррационально (например,
– иррационально (например,
![]() и т.д.), а также числа
и т.д.), а также числа
![]() .
.
Замечание 2.
Если существует биективное отображение
![]() ,
то множества
,
то множества
![]() и
и
![]() называется равномощными.
Всякое множество, равномощное множеству
называется равномощными.
Всякое множество, равномощное множеству
![]() натуральных чисел называется счетным.
Если же множество равномощно множеству
,
то говорят, что оно имеет мощность
континуума.
Еще Кантор показал, что множество
алгебраических чисел (как и множество
)
счетное, а множество трансцендентных
чисел (как и множество иррациональных)
имеет мощность континуума. Таким образом,
трансцендентных чисел гораздо «больше»,
чем алгебраических.
натуральных чисел называется счетным.
Если же множество равномощно множеству
,
то говорят, что оно имеет мощность
континуума.
Еще Кантор показал, что множество
алгебраических чисел (как и множество
)
счетное, а множество трансцендентных
чисел (как и множество иррациональных)
имеет мощность континуума. Таким образом,
трансцендентных чисел гораздо «больше»,
чем алгебраических.
Теорема 1. Если – алгебраическое число над полем , то
существует единственный нормированный неприводимый в
 многочлен
многочлен
 ,
корнем которого является число
;
,
корнем которого является число
;если – корень многочлена
 ,
то
,
то
 .
.
□ 1) Согласно
определению 1 в кольце
существует такой многочлен
,
что
![]() .
Пусть
.
Пусть
![]()
каноническое
разложение многочлена
в произведение неприводимых над полем
многочленов из
.
Так как
,
то число
является корнем, по крайней мере, одного
из нормированных неприводимых над
полем
многочленов
![]() .
Пусть
.
Пусть
![]() –
любой другой многочлен с теми же
свойствами. Так как
и
оба неприводимы, то они либо взаимно
просты, либо ассоциированы (т.е. делятся
друг на друга). Но если они взаимно просты
в кольце
,
то они взаимно просты и в кольце
–
любой другой многочлен с теми же
свойствами. Так как
и
оба неприводимы, то они либо взаимно
просты, либо ассоциированы (т.е. делятся
друг на друга). Но если они взаимно просты
в кольце
,
то они взаимно просты и в кольце
![]() ,
а это противоречит тому, что они имеют
общий корень
и, следовательно, в
они делятся на
,
а это противоречит тому, что они имеют
общий корень
и, следовательно, в
они делятся на
![]() .
Значит
и
– ассоциированы. Но поскольку они
нормированы, то они обязаны быть равными.
Таким образом, многочлен
.
Значит
и
– ассоциированы. Но поскольку они
нормированы, то они обязаны быть равными.
Таким образом, многочлен
![]() удовлетворяет требованиям 1) теоремы
1.
удовлетворяет требованиям 1) теоремы
1.
2) Пусть
– корень многочлена
из кольца
и
![]() – найденный выше многочлен. Так как
– неприводим, для любого многочлена
возможно лишь одно из двух: либо
и
взаимно простые, либо
.
Но первое невозможно, так как
и
имеют общий корень
.
Значит,
,
что и требовалось доказать. ◘
– найденный выше многочлен. Так как
– неприводим, для любого многочлена
возможно лишь одно из двух: либо
и
взаимно простые, либо
.
Но первое невозможно, так как
и
имеют общий корень
.
Значит,
,
что и требовалось доказать. ◘
Определение 2.
Нормированный неприводимый многочлен
![]() ,
для которого алгебраическое относительно
поля
число
является корнем, называется минимальным
многочленом числа
,
а степень минимального многочлена
называется степенью
алгебраического числа
.
,
для которого алгебраическое относительно
поля
число
является корнем, называется минимальным
многочленом числа
,
а степень минимального многочлена
называется степенью
алгебраического числа
.
Примеры.
Число
 является алгебраическим числом 6
степени, а минимальным для него является
многочлен
является алгебраическим числом 6
степени, а минимальным для него является
многочлен
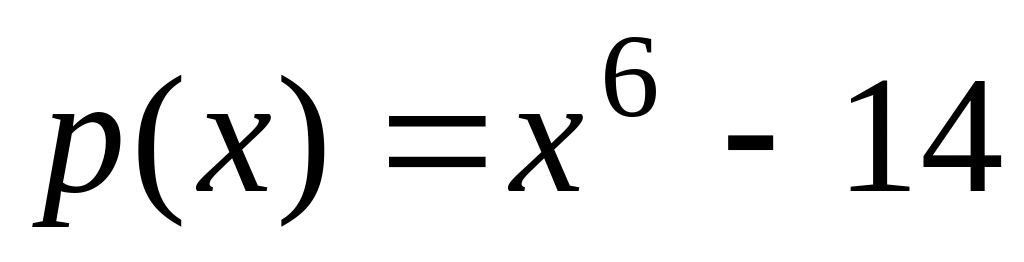 (он неприводим над полем
в силу признака Эйзенштейна).
(он неприводим над полем
в силу признака Эйзенштейна).
Всякое число
 является корнем многочлена
является корнем многочлена
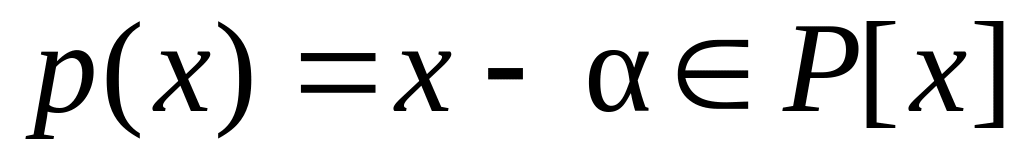 и, следовательно, является алгебраическим
относительно поля
числом степени 1. Очевидно и наоборот
– всякое алгебраическое относительно
поля
число степени 1 принадлежит полю
.
и, следовательно, является алгебраическим
относительно поля
числом степени 1. Очевидно и наоборот
– всякое алгебраическое относительно
поля
число степени 1 принадлежит полю
.
Относительно поля все действительные числа имеют степень 1, а все мнимые – степень 2 (см. пример 3).
Замечание 3.
Если
– алгебраическое относительно поля
число степени
![]() и поле
и поле
![]() является расширением поля
(т.е.
является расширением поля
(т.е.![]() ),
то
является алгебраическим относительно
поля
числом степени
),
то
является алгебраическим относительно
поля
числом степени
![]() .
Это следует из того, что неприводимый
над полем
многочлен может оказаться приводим над
его расширением. Например, число
.
Это следует из того, что неприводимый
над полем
многочлен может оказаться приводим над
его расширением. Например, число
![]() является алгебраическим числом степени
2 над полем
(минимальный многочлен
является алгебраическим числом степени
2 над полем
(минимальный многочлен
![]() )
и алгебраическим относительно поля
числом степени 1 (минимальный многочлен
)
и алгебраическим относительно поля
числом степени 1 (минимальный многочлен
![]() ).
).
Теорема 2. Если неприводим над каким-либо полем , то он не имеет в поле кратных корней.
□ В силу закона
контрапозиции достаточно доказать, что
если
и имеет кратный корень в
,
то он приводим над полем
.
Пусть
– кратный корень многочлена
.
Тогда
является также корнем его производной
![]() .
Отсюда легко следует, что
.
Отсюда легко следует, что
![]() принадлежит кольцу
и имеет положительную степень. Значит,
принадлежит кольцу
и имеет положительную степень. Значит,
![]() ,
где
,
где
![]() ,
т.е.
приводим над полем
.
◘
,
т.е.
приводим над полем
.
◘
