Теорема об изменении кинетической энергии точки.

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M₀ , где она имеет скорость  , в положение М₁ , где ее скорость равна  .

Для получения искомой зависимости обратимся к уравнению  выражающему основной закон динамики. Проектируя обе части этого равенства на касательную   к траектории точ­ки М, направленную в сторону движения, получим:

 

Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

В результате будем иметь:

 .

Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что   где   - эле­ментарная работа силы F_k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

.

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

.

Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Теорема Кенига. Кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы при ее движении относительно центра масс.

Д’Аламбера принцип — в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

Дано:  Определить: реакции подпятника и подшипника. 

Решение:

Изобразим на чертеже вал с прикрепленным к нему стержнями.    Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем координатные оси и изобразим действующие на систему силы. Согласно принципу Даламбера присоединим к этим силам силы инерции. Так как вал вращается равномерно то элементы стержня имеют только нормальные ускорения  , направленные к оси вращения.  Расстояния центров масс соответствующих частей стержня до оси вращения Ускорения центров масс 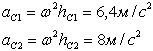   Силы инерции 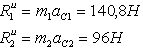Согласно принципу Даламбера приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составим для нее шесть уравнений равновесия. 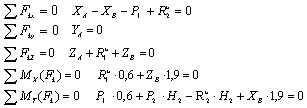 Где плечи сил равны Откуда 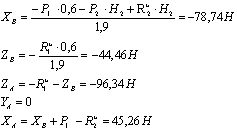Ответ:  Силы   направлены противоположно направленным на рисунке. 

Общее уравнение динамики. При движении механической системы с идеальными  связями работа всех активных сил и сил инерции на любом виртуальном перемещении системы в каждый фиксированный момент времени равна нулю:

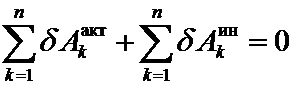
• Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения.   — угловая скорость

При вращательном движении роль массы m выполняет момент инерции I, а вместо линейной скорости v выступает угловая скорость ω, и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:

T_вр=Iω²/2

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, кинетическая энергия складывается из энергии поступательного движения и энергии вращения:

T=(mv_c²+I_cω²)/2,

где m - масса катящегося тела; v_c - скорость центра масс тела; v_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

Кинетическая энергия поступательного движения - ( m*v^2)\2

Кольца относительно оси, проходящей через его центр и перпендикулярно его плоскости - m*r^2 (m - масса, r - радиус кольца) Для диска относительно аналогичной оси (m*r^2)/2; Для стержня через ось, проходящую через него - 0. Диск относительно диаметра: (m*r^2)/4 Кольцо относительно диаметра: (m*r^2)/2 Стержень относительно оси, перпендикулярной ему и проходящей чере середину: (m*l^2)/12, где l - его длина. Стержень относительно оси, перпендикулярной ему и проходящей через конец: (m*l^2)/3.