15. Алгоритм cart. Метод Cost complexity tree pruning.

Алгоритм позволяет делать оценку поддерева, позволяя найти наилучшего для отсечения.

Основная проблема отсечения – большое количество всех возможных отсеченных поддеревьев для одного дерева.

Рассматривается отсечение, как получение компромисса между двумя проблемами:

• Получение дерева оптимального размера.

• Получение точной оценки вероятности ошибочной классификации.

Основная идея: рассматривать не все возможные отсечения дерева, а только лучшее из них, по оценке:

Сα (T) = R(T) +α |T| , где |T| - число листов дерева, R(T) –ошибка классификации дерева.

Если R(T)-const, то с увеличением дерева его полная стоимость будет увеличиваться, тогда в зависи-ти от α, меньшее дерево дающее большую ошибку может стоить меньше, чем большее дерево.

Tmax – начальное дерево.

T α – обрезанное дерево при α.

Алгоритм CART строит уменьшающуюся последовательность деревьев, начиная от Tmax и, возможно, до корня, в зависимости от α. Первое дерево последовательности – это само дерево Tmax при α=0.

Пусть S –это ветвь дерева с корнем Q.

При каких условиях дерево |T-S|>T (T-S лучше Т).

Если отсечение в узле S, тогда вклад в полную стоимость, где Сα (S) = R(S) +α |S|, R(S) – сумма ошибок всех листов поддерева. Полная стоимость дерева с корнем Q: Сα(Q) = R(Q) +α.

R(Q)=r(Q)p(Q), где r(Q) – ошибка классификации узла и p(Q) – пропорция примеров, которые прошли через дерево.

Сα(Q) = Сα(S) – уравнивание стоимостей.

R(Q)+ α = R(S) +α|S|

α=( R(Q)- R(S))/ α*(|S|-1)

Это значение вычисляется для каждого узла в дереве Tk, а затем удаляются связи, значение для которых будет являться наименьшим.

g(S)=( R(Q)- R(Tk,S))/ α*(|Tk,S|-1) – более общий вид

Общий алгоритм:

1. T1=Tmax α1=0 k=1

Пока Tk!=Q делаем

2. Для всех нетерминальных узлов вычислить gk(S)

3. α_k+1=min gk(S)

4/ обойти сверху вниз все узлы и отрезать те, для которых gk(S)= αk+1 k++

Итак, мы имеем последовательность деревьев, нам необходимо выбрать лучшее дерево из неё. То, которое мы и будем использовать в дальнейшем. Наиболее очевидным является выбор финального дерева через тестирование на тестовой выборке. Дерево, давшее минимальную ошибку классификации, и будет лучшим. Однако, это не единственно возможный путь.

16. Алгоритм сart. Выбор итогового дерева решений. Метод V-fold cross-validation.

Перекрёстная проверка – путь выбора окончательного дерева, при условии, что набор данных имеет небольшой объем или же записи набора данных несколько специфические, что разделить набор на обучающую и тестовую выборки невозможно. Этот метод применяется тогда, когда каждая запись в тестовой выборке уникальна или мала.

Строится дерево на всех данных, затем находится последовательность поддеревьев. Вся обучающая выборка разд-ся на V-групп одного размера V(5~10).

Расчёт коэфф β:

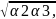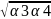(β1 = α1, β2 = β3 = , βn+1 = ∞)

На выборке Gi находится наименьшее минимизирующее поддерево для всех βk - T⁽¹⁾(βk).

Вычисляется и запоминается ошибка дерева на выборке G1: T⁽¹⁾(βk).

Для каждого βk суммировать его ошибки на выходных подвыборках Gi.

Наименьшая общая ошибка будет соответствовать наилучшему дереву: βk -> Tk.