- •1. Метод сечений. Напряжение. Растяжение, сжатие. Расчет на прочность.
- •2. Механические свойства конструктивных материалов. Диаграмма растяжения. Пределы текучести и прочности.
- •3. Кручение. Эпюры крутящих моментов. Расчет на прочность при кручении вала, определение диаметра вала.
- •4. Условие прочности вала при совместном действии крутящего и изгибающего моментов. Определение диаметра вала по теории наибольших касательных напряжений, по энергетической теории.
- •5. Расчет на жесткость при кручении вала, определение его диаметра из условия жесткости при кручении.
- •6. Геометрические характеристики сечений. Статический момент, момент инерции, момент сопротивления простых сечений.
- •7. Расчет на прочность при изгибе
- •8. Устойчивость сжатых стержней. Формула Эйлера для определения критической нагрузки, пределы её применимости.
- •9.Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры.
- •10.Продольная и поперечная деформация и перемещение стержня. Закон Гука.
- •1.2.1.Структурный синтез механизмов
- •1. 3.0. Конструктивно-функциональная классификация механизмов
- •1.4.0. Задачи и методы кинематического анализа механизмов.
- •1.5.1.Планетарные передачи. Устройство. Кинематический расчет. Теорема Виллиса.
- •Детали машин
- •1.Соединения
- •1.1.1.Резьбовые соединения.
- •1.1.2.Момент завинчивания болтового соединения.
- •1.1.3. Расчет стержня болта действием осевой при затяжке болта.
- •1.1.4. Расчет болтов, нагруженных поперечной нагрузкой
- •1.2.1.Шпоночные соединения.
- •1.2.2. Расчет призматических шпонок
- •1.3.1. Шлицевые соединения. Расчет шлицевых соединений на смятие и износ.
- •Расчет шлицевых соединений___
- •1.4.1Сварные соединения.Расчет сварных соединений встык. Расчет угловых швов.
- •2.1.1. Фрикционные передачи
- •2.2.1 Общие сведения. Ременные передачи.
- •2.2.4.Силы в ветвях ремня:
- •2.3 Цепные передачи
- •2.3.1 Общие сведения. Цепи. Материалы
- •2.3.2 Усилия в элементах передачи. Расчет передачи
- •2.5.1 Цилиндрические зубчатые передачи
- •2.5.1Геометрические и кинематические параметры:
- •2.5.1 Геометрические и кинематические параметры конических с прямам зубом передач.
- •2.5.2.Точность зубчатых передач
- •2.5.3Проектные расчёты на контактную выносливость прямозубых, косозубых и конических зубчатых передач.
- •2.5.4 Проверочные расчеты на контактную выносливости и изгибную выносливости зубьев всех видов зубчатых передач.
- •2.5.5 Силы в зацеплении прямозубых, косозубых и конических зубчатых колес. Прямозубая цилиндрическая передача
- •2.5.6 Материалы, термообработка для зубчатых колес
- •2.5.6Способы изготовления зубчатых колес
- •2.6 Червячные передачи
- •2.6.1 Общие сведения
- •2.6.2 Материалы червячных передач и их точность. Скорость скольжения.
- •2.6.3. Геометрия и кинематика червячного зацепления.
- •2.6.4Проектный расчет на контактную выносливость
- •2.6.5Проверочный расчет на контактную и изгибную выносливость зубьев червячного колеса
- •2.6.6. Тепловой расчет червячной передачи, кпд, смазывание червячной передачи.
- •2.6.7 Силы в зацеплении.
- •3.Валы и оси
- •Подшипники качения
- •4.1.1.Классификация подшипников качения. Точность, условие обозначения.
- •4.1.2. . Расчет подшипников качения на долговечность или динамическую грузоподъемностью
- •5. Общие сведения. Классификация. Выбор муфты. Знать принцип работы муфт.
- •1.Глухие муфты
- •2. Выбор упруго-компенсирующей муфты , проверочный расчёт .Эскиз муфты.
- •3. Выбор жестко-компенсирующей муфты , проверочный расчёт .Эскиз муфты.
- •4. Предохранительные муфты
- •5. Управляемые муфты
4. Условие прочности вала при совместном действии крутящего и изгибающего моментов. Определение диаметра вала по теории наибольших касательных напряжений, по энергетической теории.
Изгиб с кручением:
На изгиб с кручением работают все валы. Вал находится в сложном напряжённом состоянии от внешних нагрузок Мизг и Ткр
По теории наибольших касательных напряжений можно определить эквивалентное напряжение:
σэкв=√(σ2+4τ2)
По энергетической теории прочности:
σэкв=√(σ2+3τ2)
Условие прочности:
σэкв= ≤ [σэкв]
, где Мэкв=√(М2+Т2)
– по теории наибольших касательных
напряжений
≤ [σэкв]
, где Мэкв=√(М2+Т2)
– по теории наибольших касательных
напряжений
Мэкв=√(М2+0.75Т2) – по энергетической теории
Внешний изгибающий момент действует на вал в 2 плоскостях: в вертикальной и горизонтальной.
Диаметр вала по теории наибольших касательных напряжений:
Т.к.
Wx=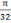 d3≈0.1d3
, то dвала
≥
d3≈0.1d3
, то dвала
≥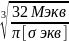 или dвала
≥
или dвала
≥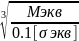
5. Расчет на жесткость при кручении вала, определение его диаметра из условия жесткости при кручении.
Расчет вала на жесткость. Во многих случаях вал должен удовлетворять не только условию прочности, но и жесткости.
За
меру жесткости при кручении принимают
относительный угол закручивания
вала. Условие жесткости бруса при
кручении состоит в том, чтобы максимальный
относительный угол закручивания не
превышал некоторого заданного допускаемого
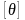
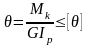 ,
,
G—коэффициент
Гука,
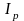 --полярный
момент инерции
--полярный
момент инерции
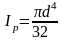 для
вала
для
вала
Допускаемый угол закручивания зависит от назначения вала и принимается в пределах 0,25...1,0 град/м.
Проверка жесткости
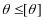 ;
;Определение предельной нагрузки
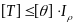 ,
должен быть известен материал и нагрузка.
,
должен быть известен материал и нагрузка.Определение геометрических параметров:
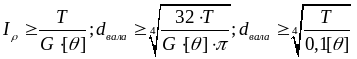
6. Геометрические характеристики сечений. Статический момент, момент инерции, момент сопротивления простых сечений.
Статические моменты плоских сечений. Сопротивление элементов различным видам деформаций зависит не только от площади, но и от формы сечения и его ориентации к направлению нагрузок. Если для исследования растяжения (сжатия) элемента достаточно знать площадь его сечения, то при исследовании изгиба и кручения необходимо иметь сведения о геометрических характеристиках сечения, существенно зависящих от его формы. К ним относятся статические моменты, моменты инерции и моменты сопротивления сечения.
С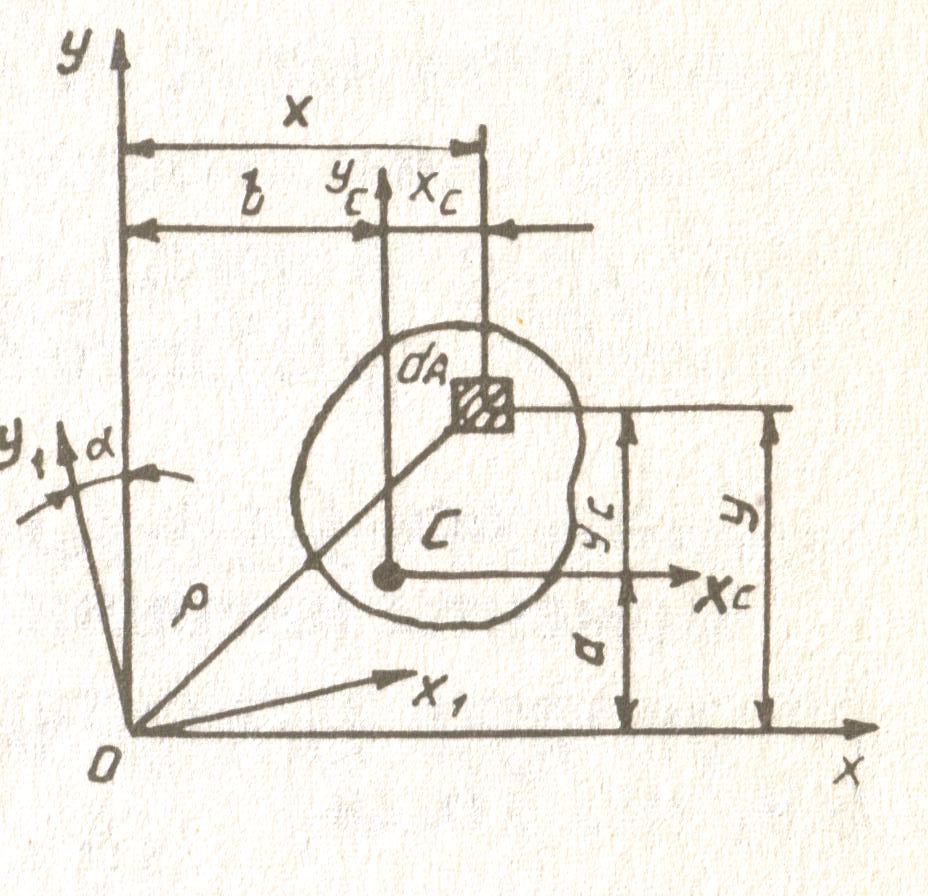 татическим
моментом сечения относительно оси
называют взятую по всей площади сумму
произведений площадей элементарных
площадок dA на расстоянии от них до этой
оси:
татическим
моментом сечения относительно оси
называют взятую по всей площади сумму
произведений площадей элементарных
площадок dA на расстоянии от них до этой
оси:
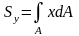 ;
;
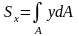
При известных
статических моментах и площади сечения
А координаты его центра тяжести можно
определить по формулам:
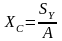 ;
;
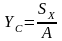
Осевые моменты
инерции.
Осевыми моментами инерции плоского
сечения относительно оси называется
взятая по всей площади сечения сумма
произведений площадей элементарных
площадок на квадраты расстояний от них
до этой оси:
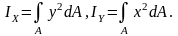 Полярный момент инерции сечения:
Полярный момент инерции сечения:
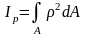 ,
где ρ – расстояние от площадки dA до
точки (полюса), относительно которой
вычисляется полярный момент инерции.
Очевидно, что:
,
где ρ – расстояние от площадки dA до
точки (полюса), относительно которой
вычисляется полярный момент инерции.
Очевидно, что:
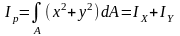 .
Центробежный момент инерции сечения
относительно двух взаимно перпендикулярных
осей:
.
Центробежный момент инерции сечения
относительно двух взаимно перпендикулярных
осей:
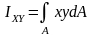
Моменты сопротивления сечений.
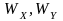 [мм3,
м3]
– осевой момент сопротивления сечения
относительно оси
[мм3,
м3]
– осевой момент сопротивления сечения
относительно оси
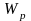 [мм3,
м3]
– полярный момент сопротивления сечения
[мм3,
м3]
– полярный момент сопротивления сечения
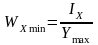 ;
;
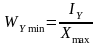 ;
;
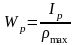
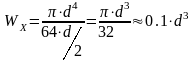 ;
;