
- •1.Комбинаторика. История возникновения комбинаторики.
- •4. Задачи комбинаторики
- •2. Основные комбинаторные принципы (Андерсон, Джеймс а.)
- •3. Теорема 8.1. (Комбинаторный принцип умножения)
- •4. Комбинаторный принцип сложения.
- •Комбинаторный принцип сложения для пересекающихся множеств.
- •6.Перестановка
- •7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
- •7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
- •7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
- •9. Рекуррентные соотношения. Числа Фибоначчи. Решение рекуррентного соотношения второго порядка.
- •9. Рекуррентные соотношения. Числа Фибоначчи. Решение рекуррентного соотношения второго порядка.
- •12. Формирование перестановок и сочетаний. Лексикографический порядок.
- •14. Обобщенные перестановки и сочетания.
- •Перестановки и сочетания с повторением.
7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
ТЕОРЕМА 8.38. (Биномиальная теорема). Для произвольного положительного целого числа n справедливы равенства

ДОКАЗАТЕЛЬСТВО.
Поскольку
arbn-r
получено в результате r-кратного
выбора а
и
n–r
-кратного
выбора b
из
n
сомножителей
в выражении (а
+ b)n,
то
коэффициент при arbn–r
равен
числу способов r-кратного
выбора а
из
n
сомножителей![]() .Второе
равенство следует из того факта, что
.Второе
равенство следует из того факта, что
![]()
ПРИМЕР 8.39. Построим разложение (2х + 3у2)4. Используя биномиальную теорему, находим
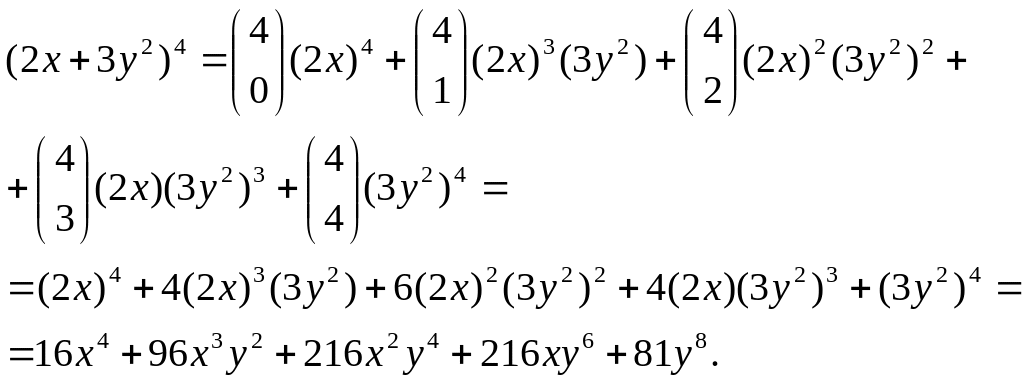
7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
Треугольник Паскаля
Теорема, в частности, дает возможность построить треугольник Паскаля. В доказательстве, приведенном ниже, использована комбинаторная техника. Доказываем теорему, используя метод математической индукции.
ТЕОРЕМА 8.42. Для всех целых чисел r и n таких, что 1 < r < n-1, С(n,r) = С(n – 1, r – 1) + С(n –1, r).
ДОКАЗАТЕЛЬСТВО. Пусть т – один из n объектов, из которых требуется выбрать r объектов. Из С(n,r) способов, которыми можно выбрать r объектов, рассмотрим то количество случаев, когда т является одним из выбранных объектов, и количество случаев, когда т выбранным объектом не является. Их сумма должна равняться С(n,r). (Почему?) Сначала рассмотрим количество случаев, когда т – один из выбранных объектов. Поскольку т уже выбрано, требуется выбрать r – 1 объект из n – 1 объектов. Существует С(n – 1,r – 1) способов сделать этот выбор. Далее рассмотрим количество способов, при которых т не является одним из выбранных объектов. По-прежнему требуется выбрать r объектов, но теперь из n – 1 объектов, учитывая, что т не может быть выбран. Другими словами, существует только n–1 объектов, из которых выбираются r объектов. Таким образом, существуют С(n–1,r) способов сделать такой выбор. Складывая количество способов выбора в обоих случаях, получаем С(n,r) = С(n – 1, r – 1) + С (n – 1,r).
 Диаграмма,
изображенная на рис. 8.10, известна как
треугольник
Паскаля.
Каждый
из внутренних элементов треугольника
равен сумме двух элементов, расположенных
над ним, что является прямым следствием
доказанной выше теоремы.
Имеем
Диаграмма,
изображенная на рис. 8.10, известна как
треугольник
Паскаля.
Каждый
из внутренних элементов треугольника
равен сумме двух элементов, расположенных
над ним, что является прямым следствием
доказанной выше теоремы.
Имеем
![]() В
первом случае n
=
2иr=
1, а во втором случае n
= 3 и
r
=
2.
Можно заметить, что (n
+ 1)-ый
ряд состоит из коэффициентов разложения
(а
+ b)n.
Например,
В
первом случае n
=
2иr=
1, а во втором случае n
= 3 и
r
=
2.
Можно заметить, что (n
+ 1)-ый
ряд состоит из коэффициентов разложения
(а
+ b)n.
Например,
![]() Эти
коэффициенты приведены в пятом ряду
треугольника. На рис. 8.11 изображен
треугольник
Паскаля с вычисленными элементами.
Эти
коэффициенты приведены в пятом ряду
треугольника. На рис. 8.11 изображен
треугольник
Паскаля с вычисленными элементами.

7. Биномиальная теорема. Треугольник Паскаля. Теорема Вандермонда.
ТЕОРЕМА 8.44. (Вандермонд) Пусть т, n и r – положительные целые числа такие, что r < min (m, n). Тогда
![]()
ДОКАЗАТЕЛЬСТВО. Левая часть равенства выражает количество способов выбора r объектов из т + n объектов. Каким бы образом мы не выбирали r объектов из т + n объектов, для некоторого 0 < k < r всегда k объектов выбираются из т объектов и r – k объектов выбираются из n объектов. Для этого существуют
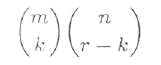
способов.
Обратно, если k
объектов для любого 0
<
k
<
r
выбираются
из m
объектов
и r
– k
объектов
выбираются из n
объектов,
то при этом r
объектов выбираются из m + n
объектов.
Следовательно, Следующее
утверждение позволяет находить сумму
квадратов чисел, образующих
строку треугольника Паскаля.
Следующее
утверждение позволяет находить сумму
квадратов чисел, образующих
строку треугольника Паскаля.
СЛЕДСТВИЕ
8.45. Для
любого положительного целого числа n
ДОКАЗАТЕЛЬСТВО. Полагая в предыдущей теореме n = m = r, получаем

8. Теорема Муавра. Выражение степеней косинусов и синусов от аргумента x через косинусы и синусы от аргументов nx и наоборот.
ТЕОРЕМА 11.9. Для углов и (cos() + isin())(cos() + isin(/)) = (cos( + ) + isin( + )).
ДОКАЗАТЕЛЬСТВО. (cos() + isin())(cos() + isin(/)) = cos() cos() + i2 sin() sin() + i sin() cos() + i sin() cos() = cos() cos() – sin() sin() + i(sin() cos() + cos() sin()) = cos( + ) + i sin( + ).
Из этой теоремы следует, что (cos() + isin())2 = cos(2) + isin(2). Попробуйте доказать следующую теорему, используя метод индукции.
ТЕОРЕМА 11.10. (Муавр) Для произвольного угла имеет место равенство (cos()+isin())k = cos(k) + isin(k).
Нам
необходимо еще одно свойство комплексных
чисел. Рассмотрим комплексное
число а
+ bi
как
изображено на рис. 11.1.
 По
теореме Пифагора
По
теореме Пифагора
![]() .
По определению
.
По определению![]() a
a
![]() ,поэтому
,поэтому![]() .
.
Таким
образом, любое комплексное число может
быть преобразовано к виду
![]() .
Из приведенной выше теоремы далее
следует, что (а+bi)n=((cos()+isin()))n
=
n(cos(n)
+ isin(n)).
.
Из приведенной выше теоремы далее
следует, что (а+bi)n=((cos()+isin()))n
=
n(cos(n)
+ isin(n)).
