
Билет 18.
Центральное растяжение-сжатие: напряжения в поперечных и наклонных сечениях стержня. Закон Гука.
Закон: Перемещение точек тела
пропорционально приложенным нагрузкам.
В поперечных сечениях бруса при
центральном растяжении-сжатии нормальные
напряжения равны отношению продольной
силы к площади поперечного сечения:
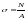 или относительная продольная деформация
прямо пропорциональна нормальному
напряжению
или относительная продольная деформация
прямо пропорциональна нормальному
напряжению
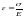 ,
откуда
,
откуда
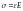 ,
где Е – модуль упругости материала, ε
– относительная линейная деформация.
,
где Е – модуль упругости материала, ε
– относительная линейная деформация.
Закон для деформации сдвига: Касательные
напряжения
 при
сдвиге прямо пропорциональны угловой
деформации:
при
сдвиге прямо пропорциональны угловой
деформации: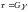 .
.
Коэффициент пропорциональности
 называется модулем сдвига или модулем
упругости второго рода. Модуль сдвига
как и модуль упругости при растяжении
имеет размерность напряжений, т.е. МПа,
кгс/см2.
называется модулем сдвига или модулем
упругости второго рода. Модуль сдвига
как и модуль упругости при растяжении
имеет размерность напряжений, т.е. МПа,
кгс/см2.
Напряжения определяются как:
 –
сила, равная произведению напряжения
–
сила, равная произведению напряжения
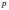 на площадь наклонного сечения
на площадь наклонного сечения
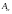 :
:
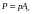
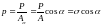

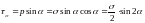
Билет 19.
Центральное растяжение-сжатие: кинематические и температурные деформации и перемещения. Потенциальная энергия деформации.
При повышении температуры у большинства материалов механические характеристики прочности уменьшаются, а при понижении температуры – увеличиваются
Удлинение (деформация) стержня при
нагревании определяется по формуле
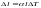 ,
где
,
где
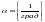 - коэффициент линейного расширения
материала стержня,
- коэффициент линейного расширения
материала стержня,
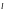 - длина стержня, ∆Т - изменение температуры.
Возникающее в поперечном сечении
нормальное напряжение
- длина стержня, ∆Т - изменение температуры.
Возникающее в поперечном сечении
нормальное напряжение
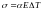 .
При понижении температуры происходит
укорочение стержня и возникают напряжения
сжатия.
.
При понижении температуры происходит
укорочение стержня и возникают напряжения
сжатия.
Потенциальная энергия деформации: Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде: A = U + K При действии статических нагрузок К = 0, следовательно: A = U Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружинах часовых механизмов, в амортизирующих рессорах и др.
Билет 20.
Центральное растяжение-сжатие: закон Гука, модуль упругости, коэффициент Пуассона, концентрация напряжений.
Закон: Перемещение точек тела
пропорционально приложенным нагрузкам.
В поперечных сечениях бруса при
центральном растяжении-сжатии нормальные
напряжения равны отношению продольной
силы к площади поперечного сечения:
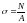 или относительная продольная деформация
прямо пропорциональна нормальному
напряжению
или относительная продольная деформация
прямо пропорциональна нормальному
напряжению
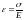 ,
откуда
,
откуда
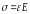 ,
где Е – модуль упругости материала, ε
– относительная линейная деформация.
Касательные напряжения
при
сдвиге прямо пропорциональны угловой
деформации:
.
,
где Е – модуль упругости материала, ε
– относительная линейная деформация.
Касательные напряжения
при
сдвиге прямо пропорциональны угловой
деформации:
.
Коэффициент пропорциональности называется модулем сдвига или модулем упругости второго рода. Модуль сдвига как и модуль упругости при растяжении имеет размерность напряжений, т.е. МПа, кгс/см2.
Модуль упругости материала показывает способность материала сопротивляться линейным деформациям. Обозначается как Е и измеряется в МПа (или паскалях).
Коэффициент Пуассона μ (поперечного сжатия) характеризует поперечное сжатие тела при одноосном растяжении к продольному удлинению; равен абс. значению отношения величины относительной поперечной деформации тела к его относительной продольной деформации μyx = εу/εх, μzx =εz/εx, где εx, εу, εz — деформации по соответствующим осям. Для изотропных тел К. П. остается постоянным при смене растяжения сжатием и смене осей деформации; в анизотропных телах в последнем случае оказывается различным. К. П. изменяется в небольших пределах — от 0,10 до 0,40.
Концентрацией напряжений называется явление возникновения значительных местных напряжений, а причина, вызвавшая концентрацию - концентратором напряжений. Концентрация напряжений характеризуется коэффициентом концентрации α. Величину α также называют теоретическим коэффициентом концентрации. Коэффициентом концентрации α называется отношение действительного напряжения σmax в наиболее напряженной точке к номинальному напряжению σn в той же точке, т. е. α = σ мах/σ n или α = τ max/τ n.
