11.Базис пространства : Разложение вектора по произвольному базису.

Базисом в пространстве называется любая система из n- линейно независимых векторов. Каждый вектор из , не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е разложить по базису.

Пусть B={ , , , ,… }- базис пространства . Тогда найдутся такие числа , что

B=

Коэффициенты разложения , называются координатами вектора b в базисе. Если задан бвзис, то коэффициенты вектора определяются однозначно

12. Различные виды уравнения прямой на плоскости. Угол между прямыми.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А² + В² не равно 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

Для решение задач уравнений используют специальный вид уравнения прямой.

Векторное параметрическое уравнение прямой

Векторное параметрическое уравнение прямой задается вектором   конец которого лежит на прямой, и направляющим вектором прямой   Параметр   пробегает все действительные значения.

]Параметрические уравнения прямой

Параметрические уравнения прямой могут быть записаны в виде:

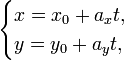
где   — производный параметр,   — координаты   и   направляющего вектора прямой. При этом

Каноническое уравнение прямой

Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:

где   — координаты   и   направляющего вектора прямой,   и   координаты точки, принадлежащей прямой.

Угол межу прямыми:

Пусть прямые   и   заданы каноническими уравнениями   и   Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: 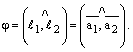  Тогда

Если   то 

Если  , то   или    .

13. Прямая и плоскость в пространстве.

1. Условия параллельности и перпендикулярности.

Пусть заданы прямая:

И плоскость: Ах + Ву + С = 0

Прямая параллельная плоскости в том и только в том случае, когда ее направляющий вектор a={l; m; n} перпендикулярен нормальному вектору N= { A; B; C} плоскости. Отсюда получаем условие параллельности прямой и плоскости: Al+Bm+Cn=0

Прямая перпендикулярна плоскости в том и только в случае, когда ее направляющий вектор коллинеарен нормальному вектору плоскости. Отсюда получаем условие перпендикулярности прямой и плоскости:

2.Угол между прямой и плоскостью:

14.Основная задача линейного программирования. Геометрический метод решения задачи лп с двумя переменными.

Основная задача линейного программирования состоит в следующем. Задана система 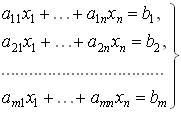 (6.10) m линейных алгебраических уравнений с n неизвестными x₁,...,x_n и линейная форма относительно этих же неизвестных: F = c₁x₁ + ... + c_nx_n. (6.11) Требуется среди всех неотрицательных решений системы (10) выбрать такое, при котором форма F принимает наименьшее значение (минимизируется). Определение: Система (6.10) называется системой ограничений данной задачи.  Сами равенства (6.10) называются ограничениями-равенствами. Отметим, что кроме ограничений-равенств в основу задач входят также ограничения-неравенства x₁≥0,...,x_n≥0 Определение: Всякое неотрицательное решение x₁⁽⁰⁾,...,x_n⁽⁰⁾(x_i⁽⁰⁾≥0; i=1,...,n) системы (6.10) назовем допустимым. Допустимое решение часто называют планом задачи линейного программирования. Определение: Допустимое решение системы (6.10), минимизирующее форму F, назовем оптимальным.

Геометрический метод решения задачи ЛП с двумя переменными.

 (8)

является полуплоскость. Для того, чтобы определить, какая из двух полуплоскостей соответствует этому неравенству, нужно привести его к виду   или  . Тогда искомая полуплоскость в первом случае расположена выше прямой a₀ + a₁x₁ + a₂x₂ = 0, а во втором - ниже нее. Если a₂=0, то неравенство (8) имеет вид  ; в этом случае получим либо   - правую полуплоскость, либо   - левую полуплоскость.

 

Областью решений системы неравенств является пересечение конечного числа полуплоскостей, описываемых каждым отдельным неравенством. Это пересечение представляет собой многоугольную область G. Она может быть как ограниченной, так и неограниченной и даже пустой (если система неравенств противоречива).

Область решений G обладает важным свойством выпуклости. Область называется выпуклой, если произвольные две ее точки можно соединить отрезком, целиком принадлежащим данной области. На рис.  показаны выпуклая область G₁ и невыпуклая область G₂. В области G₁ две ее произвольные точки А₁ и В₁ можно соединить отрезком, все точки которого принадлежат области G₁. В области G₂ можно выбрать такие две ее точки А₂ и В₂, что не все точки отрезка А₂В₂принадлежат области G₂.

Опорной прямой называется прямая, которая имеет с областью по крайней мере одну общую точку, при этом вся область расположена по одну сторону от этой прямой. На рис.  показаны две опорные прямые l₁ и l₂, т. е. в данном случае прямые проходят соответственно через вершину многоугольника и через одну из его сторон.