Билет 9. Скалярное произведение векторов и его свойства. Длина вектора, угол между векторами.

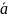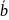Скалярным произведением двух ненулевых векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов нулевой, то угол не определен и скалярное произведение по определению полагают равным 0.

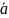* = ǀ ǀ*ǀ ǀ*cosɕ, где ɕ - угол между векторами и

Свойства скалярного произведения.

1. Свойство перестановочности сомножителей

а ̅ * b ̅ = b ̅ * а ̅

2. Свойство сочетательности относительно умножения на число

(ƛ а ̅)* b ̅ = ƛ (а ̅* b ̅)

3. Свойство распределительности суммы вектором

* ( * )= * + *

4. * = ǀ ǀ²

Расстояние между началом и концом вектора называется его длиной и обозначается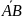 ǀ ǀ или ǀ ǀ

Длина вектора на плоскости вычисляется по следующей формуле:

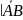ǀ

Длина вектора в трехмерном пространстве вычисляется по следующей формуле:

ǀ

Формула длины вектора в n-мерном пространстве:

Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

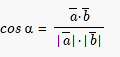
Билет 10. Линейно зависимые и линейно не зависимые системы векторов.

Пусть имеем векторное пространство V и систему векторов A={ } (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор называется линейной комбинацией системы векторов A. Если все скаляры , то такая комбинация называется тривиальной (простейшей), (и ). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной.

• Определение 1: система векторов A называется линейно-независимой, если только тривиальная линейная комбинация векторов системы равна 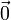, (т.е. )

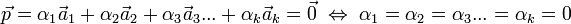• Определение 2: система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная .