
- •Система линейных уравнений. Основные понятия. Метод Гаусса.
- •Определители 2-го и 3-го порядков, их свойства
- •Определители n-го порядка и их свойства
- •Матрицы и действия с ними. Свойства операций над матрицами.
- •Билет 6. Обратная матрица и способы ее нахождения
- •Билет 7. Решение систем линейных уравнений с помощью формул Крамера и с помощью обратной матрицы.
- •Билет 8. Векторы и линейные операции над ними. Арифметическое n-мерное векторное пространство Rn. Геометрический смысл пространств r2 и r1
- •Билет 9. Скалярное произведение векторов и его свойства. Длина вектора, угол между векторами.
- •Билет 10. Линейно зависимые и линейно не зависимые системы векторов.
Билет 6. Обратная матрица и способы ее нахождения
Обра́тная ма́трица — такая матрица (А-1), что их умножение (с любой стороны) даст в результате единичную матрицу
![]()
Свойства обратной матрицы
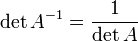 ,
где
,
где
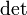 обозначает
определитель.
обозначает
определитель. для
любых двух обратимых матриц
для
любых двух обратимых матриц
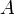 и
и
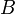 .
.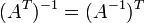 где
где
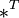 обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу.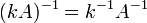 для
любого коэффициента
для
любого коэффициента
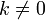 .
.Если необходимо решить систему линейных уравнений
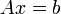 ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где
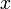 —
искомый вектор, и если
—
искомый вектор, и если
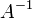 существует,
то
существует,
то
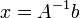 .
В противном случае либо размерность
пространства
решений больше нуля, либо их нет вовсе.
.
В противном случае либо размерность
пространства
решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Нахождение обратной матрицы с помощью присоединенной
(АǀЕ) ̴ (ЕǀА-1)
Пример. С помощью элементарных преобразований строк найти обратную матрицу к матрице A.
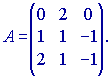
Определитель равен –2, следовательно существует обратная матрица. Припишем к исходной матрице единичную, и будем преобразовывать матрицу A, к виду единичной матрицы. Тогда единичная матрица преобразуется в обратную к матрице A.
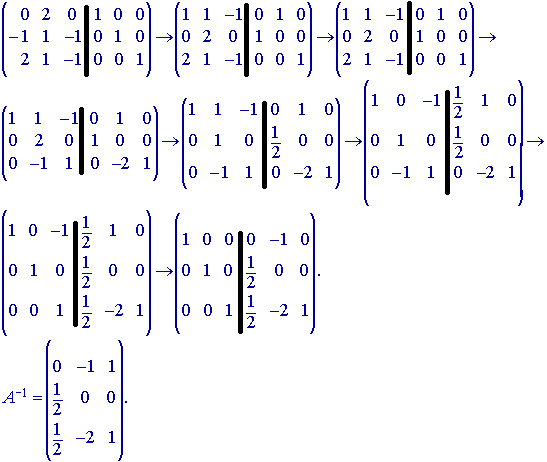
Нахождение обратной матрицы по формуле:
Пример.
Найдите обратную матрицу для
матрицы
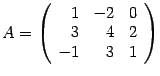 Решение.
Находим определитель
Решение.
Находим определитель
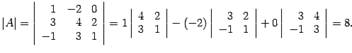 Так
как
Так
как
![]() то
матрица А - невырожденная, и обратная
для нее существует. Находим алгебраические
дополнения:
то
матрица А - невырожденная, и обратная
для нее существует. Находим алгебраические
дополнения:
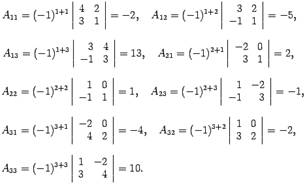 Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй - строке:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй - строке:
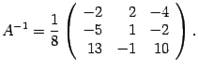 Полученная
матрица и служит ответом к задаче.
Полученная
матрица и служит ответом к задаче.
Билет 7. Решение систем линейных уравнений с помощью формул Крамера и с помощью обратной матрицы.
АХ=В
Умножим на А-1 обе части уравнения
А-1 * А * Х = А-1 *В
ЕХ = А-1В
Х![]() = А-1В
= А-1В
5х1 + 10х2 = 4
3х1 – х2 = 1
А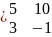 ;
;
В =
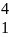 ;
;
Х =

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и оно единственно)

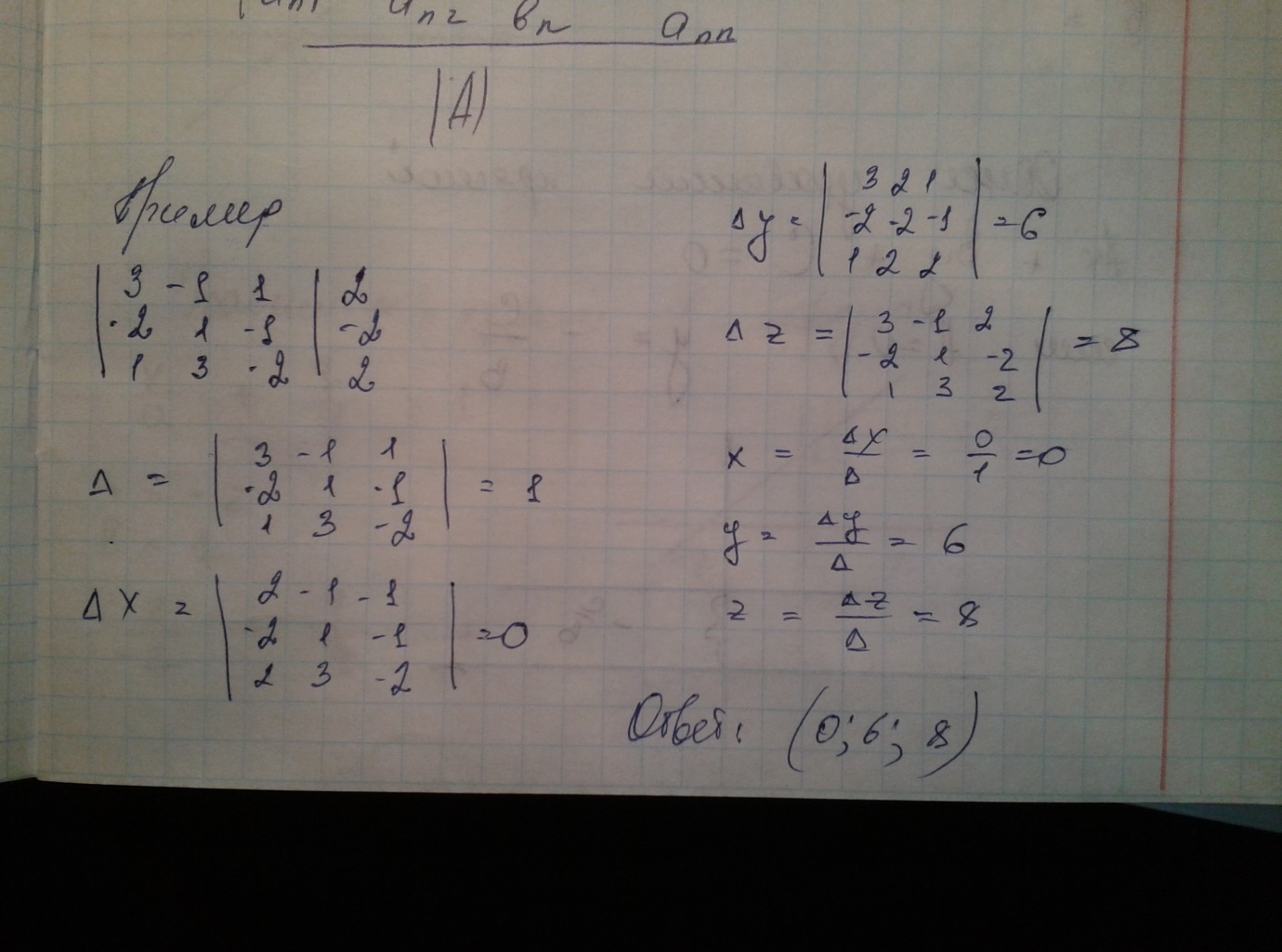
Билет 8. Векторы и линейные операции над ними. Арифметическое n-мерное векторное пространство Rn. Геометрический смысл пространств r2 и r1
Вектором называется направленный отрезок.
Линейными
операциями
называются операции сложения и
вычитания векторов и умножения
вектора на число.
1. Сумма
![]() векторов
векторов
![]() и
и
![]() находится
по правилу
треугольника
находится
по правилу
треугольника
 или
по правилу
параллелограмма
или
по правилу
параллелограмма

— эти правила равносильны.
Сложение
векторов
коммутативно и ассоциативно:
![]()
![]()
2.
Разность векторов
![]() можно
определить как сумму
можно
определить как сумму
![]() ,
т. е. вычитание заменяется прибавлением
противоположного вектора.
Удобно
также правило
треугольника:
векторы
и
откладывают
от общего начала, тогда разность
есть
вектор, начало которого совпадает с
концом
,
а конец — с концом
,
т. е. вычитание заменяется прибавлением
противоположного вектора.
Удобно
также правило
треугольника:
векторы
и
откладывают
от общего начала, тогда разность
есть
вектор, начало которого совпадает с
концом
,
а конец — с концом
 3.
Произведением
3.
Произведением
![]() (или
(или ![]() )
вектора
на
действительное число λ называется
вектор
,
коллинеарный вектору
,
имеющий длину, равную
)
вектора
на
действительное число λ называется
вектор
,
коллинеарный вектору
,
имеющий длину, равную
![]() ,
и то же направление, что и вектор
,
если λ >
0, и направление, противоположное
направлению вектора
,
если λ <
0.
Так, например,
,
и то же направление, что и вектор
,
если λ >
0, и направление, противоположное
направлению вектора
,
если λ <
0.
Так, например,
![]() есть
вектор, имеющий то же направление, что
и вектор
,
а длину, вдвое большую, чем вектор
(рис.
108).
есть
вектор, имеющий то же направление, что
и вектор
,
а длину, вдвое большую, чем вектор
(рис.
108).
 В
случае, когда λ = 0 или
В
случае, когда λ = 0 или
![]() ,
произведение
представляет
собой нулевой вектор.
,
произведение
представляет
собой нулевой вектор.
Противоположный
вектор
![]() можно
рассматривать как результат умножения
вектора
на
λ = -1:
можно
рассматривать как результат умножения
вектора
на
λ = -1:
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
Множество всех векторов размерности n называется арифметическим n-мерным векторным пространством и обозначается Rn.
Геометрический смысл имеют лишь пространства R1, R2, R3 . Для R1 – это прямая, для R2 – плоскость, для R3 – трехмерное пространство.
