Вопрос 12замена переменной в определенном интеграле.Интегрирование по частям

1 метод замены переменной(метод подстановки)

Т.если ф-я y=f(x) непрерывна на отрезке [a;b] а ф-я x=v(t) непрерывно дифф на отрезке [

V(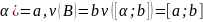

Интеграл от а до в

Пример: ( x=rsint x=0 t=0 dx=rcostdt x=r t=π/2 ) =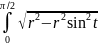 rcostdt=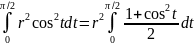

Метод интегрирования по частям

Т.u-u(x) v-v(x) непрерывно дифф на отрезке [a;b] тогда справедлива формула 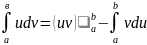формула интегрирования по частям в опред интеграле(uv’)=u’v+uv’

Пример: =(uv)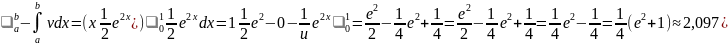

Вопрос 13Несобственные интегралы с бесконечными пределами и от неограниченных функций

О п р е д е л е н и е. Интегралы с бесконечными пределами или от неограниченных функций называются несобственными.

Несобственные интегралы с бесконечными пределами

Несобственный интеграл от функции f(x) в пределах от а до+∞ определяется равенством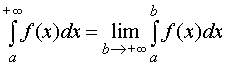

Если предел (67) существует и конечен, то несобственный интеграл называется сходящимся. Если предел (67) не существует или равен бесконечности, то интеграл называется расходящимся.

Эти правила действуют и в других случаях, когда бесконечным является нижний предел интегрирования:

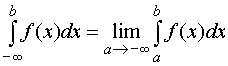
или оба предела интегрирования бесконечны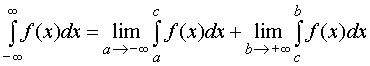

где с – произвольное вещественное число.

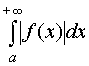О п р е д е л е н и е. Если наряду с интегралом сходится и интеграл то интеграл называют абсолютно сходящимся, а функцию f (x) – абсолютно

Пример 1. Вычислить несобственный интеграл или установить его расходимость:

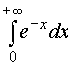
Решение. Используя формулу (67), имеем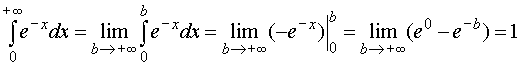

Следовательно, данный несобственный интеграл сходится и равен 1.

Вопрос 16 дифференциальные ур-я первого порядка.Основные понятия

опр.: Дифференциальное Ур-е вида y’=f(x,y) или F(x,y,y’)=0, где x – независимая переменная, y=y(x), а y’ – ее производная по переменной x, называется дифференциальным уравнением первого порядка. опр.: Решением (частным решением) дифф. ур-я первого порядка на (a,b) называется ф-я y=φ(x), при подстановке которой вместе с ее производной в дифф. ур-е, получается тождество, выполняемое на всей (a,b). Ур-е Ф(x,y)=0, неявно задающее это решение, наз-ся интегралом (частным интегралом) дифф. ур-я первого порядка. опр.: Ф-я y= φ(x,C) наз-ся общим решением дифф. ур-я первого порядка, если 1) при каждом допустимом значении параметра С эта ф-я явл. частным решением этого дифф. ур-я; 2) каждое частное решение можно записать в виде y= φ(x,C0) при некотором значении параметра С=С0. Ур-е Ф(x,y,C)=0, неявно задающее общее решение дифф. ур-я первого порядка, наз-ся общим интегралом этого дифф. ур-я.

Вопрос17Теорема о существовании и единственного решения дифф ур-я 1-го порядка

опр.: Задача Коши для дифф. ур-я это задача нахождения частного решения этого ур-я, удовлетворяющего начальному условию теорема о существовании и единственности задачи Коши: Пусть у дифф. ур-я функция непрерывна в области D плоскости xOy и ограничена в D. Тогда сущ-ет и единственно на промежутке частное решение этого ур-я удовл. начальному условию замечание: Кривая на которой ф-я - частное решение дифф. ур-я наз-ся интегральной кривой. След-но в услових теоремы через точку единственная интегральная кривая этого ур-я. опр.: Точки области D, в которых нарушается единственность решения задачи Коши, наз-ся особыми точками дифф. ур-я. опр.: Решение дифф. ур-я в каждой точке которого нарушается единственность решения задачи Коши, наз-ся особым решением этого ур-я. особые решения не получаются из общего решения ни при каких значениях параметра C. нахождение особого значения: 1) Если общее решение дифф. ур-я, то особое решение находится из системы исключением параметра C (причем надо проверить, что это решение) 2) Если Ф(x,C)=0 – общий интеграл дифф. 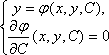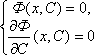ур-я, то особое решение находится из системы исключением параметра C (причем надо сделать проверку)