
- •Вопрос 1
- •Вопрос2
- •Вопрос 3таблица соновных формул и правил интегрирования
- •Вопрос 4Основные етоды интегрирования:непосредственное,замена переменной и по частям
- •Вопрос 9
- •Вопрос 10
- •Вопрос 12замена переменной в определенном интеграле.Интегрирование по частям
- •Вопрос 13Несобственные интегралы с бесконечными пределами и от неограниченных функций
- •Вопрос 16 дифференциальные ур-я первого порядка.Основные понятия
- •Вопрос17Теорема о существовании и единственного решения дифф ур-я 1-го порядка
- •Вопрос20Дифференцированые ур-я второго порядка
- •Вопрос21Дифференц ур-я второго порядка доп пониж порядка
- •Вопрос19Линейный дифференциальные уравнения первого порядка
Вопрос 1
Первообразная функция и неопределенный интеграл
Зная закон движения тела, можно, продифференцировав функцию перемещения тела по времени, в любой момент найти его скорость. Часто требуется решить обратную задачу, то есть найти перемещение тела, зная, как изменяется его скорость. Эта и подобные задачи решаются при помощи интегрирования – операции, обратной дифференцированию.
Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого х€D F’(x)=f(x)
Так, функция F= является первообразной функции F(x)=f(x)
в чем можно убедиться, поставив эти
функции в определение первообразной.
Функция F=
является первообразной функции F(x)=f(x)
в чем можно убедиться, поставив эти
функции в определение первообразной.
Функция F=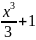 также является первообразной функции
F(x)=
также является первообразной функции
F(x)=
Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f.
Таким образом, для любой функции ее первообразная F определяется неоднозначно. Для того, чтобы задать ее однозначно, нужно указать точку A (x0; y0), удовлетворяющую уравнению y = F(x)
Пусть дана ф-я f(x) которая определна на некотором интервале (а:в) или отрезке [a;b].Ствится вопрос а существует ли такая ф-я f(x) а если существует как ее найти,чтобы выполнилось условие F’(x)=f(x)для x€(a;b).Пример: F(x)=2x f(x)=
F”(x)=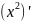 =2x=F(x)
для любого х€R
=2x=F(x)
для любого х€R
Действие нахождения первообразной ф-и наз ее интегрированием.эта операция обратная
Т1.Если F(x) есть первообр ф-я F(x) на интервале (а;в) то и ф-ии Ф(х)=F(x)+c,c=const, также явл первообразной для ф-ииF(x)
Т2.если ф-я F(x)на интервале (а;в) то всякая другая первообр для ф-ии F(x) опред формулой:Ф(х)=F(x)+c c=const т.е. любые 2 первообр для ф-ии F(x) отл м-у собой на постоянную
Т3 для любой непрерыв ф-ии на отрезке [a;d] существ не неопред интеграл но он может не выражаться элементарной ф-ей
допечатать
Вопрос2
Основные свойства неопределенного интеграла
1)Если ф-я f(x) имеет
первообразную на промежутке X, и k –
число, то
2) Если функции f
( x ) и g
( x ) имеют первообразные
на промежутке X , то![]()
3) Если функция f
( x ) имеет первообразную
на промежутке X , то для
внутренних точек этого промежутка:
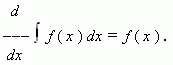
4) Если функция f
( x ) непрерывна на промежутке
X и дифференцируема во
внутренних точках этого промежутка,
то:
![]()
Вопрос 3таблица соновных формул и правил интегрирования
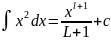
2)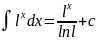 3)
3)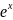 dx=
=c
4)
dx=
=c
4) =ln/x/+c
5)sinxdx=-cos+c 6)cosxdx=sinx+c
=ln/x/+c
5)sinxdx=-cos+c 6)cosxdx=sinx+c
6)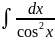 =tgx+c
7)
=tgx+c
7)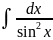 =-ctgx+c
8)
=-ctgx+c
8)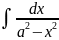 9)
9)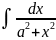
10) 11)
11)

Известны так называемые неберущиеся интегралы
1) dx
интеграл пуасона 2)
dx
интеграл пуасона 2) dx
интегральный sin
dx
интегральный sin
3) ) итнегральный cos 4)
итнегральный cos 4) интегральный ln
интегральный ln
6)

5)
Вопрос 4Основные етоды интегрирования:непосредственное,замена переменной и по частям
Непосредственное интегрировани е интегр путем подвод подинтегральной ф-ии в табл форме
 dx=
dx= dx=
dx= dx=
-
dx=
- =tgx-x+c
=tgx-x+c
Метод подстановки(замены переменной)
Т.Если ф-я х=µ(t) монотнна и непрерывна диференц в промежуткеα<µ(t)<b то имеет место ф-ла для всякой ф-ии f(x)интегрир по интервал (а;в)
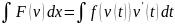
Метод интегрирования по частям
Пусть имеется 2 ф-и
u=u(x) v=v(x)которые непрерывно
дифф на интервале (а;в) тогда справедлива
ф-ла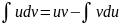
В8Задачи приводящие к понятию определенного интеграла
Пусть на [a,d]задана ф-я у=f(x) f(x)≥0
Криволинейн трап будем называть фигуру огран след линиями:
1)прямыми х=а,х=в
2)y=f(x) и осью ох аАВв-криволинейная трапеция A(a;f(a)) B(b;f(b))
Требуется определить S трапец для этого разобьем отрезок [ab] на n частей
a= <
<
n-1 точки
разбиения [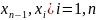
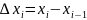
тогда а криволинейная трапеция разбивается на n малых криволин трап
2)на каждом из участков
разбиения выбираем произв тчку
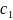 на [
на [ ]
и вычисляем значение в этой точке f
]
и вычисляем значение в этой точке f
Тогда S=
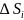 площадь
риволинейных трапеций ,плоученных в
ходе разбиения
площадь
риволинейных трапеций ,плоученных в
ходе разбиения

4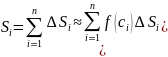
S= где
где
 диаметр
разбиения отрезка АВ
диаметр
разбиения отрезка АВ
