
- •Вопрос1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Вопрос 5
- •Вопрос 6
- •Связь с градиентом
- •Вопрос 7
- •Тейлора формула
- •Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •Вопрос 8
- •Описание метода
- •Вопрос 9
- •Вопрос 10 Криволинейный интеграл
- •Вопрос 11
- •Вопрос 12
- •Вопрос 13
- •Поверхностный интеграл первого рода Определение
- •Параметрическая форма
- •Свойства
- •Поверхностный интеграл второго рода Определение
- •Связь между поверхностными интегралами второго и первого рода
- •Свойства
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16 Примеры физических задач, приводящих к уравнениям с разделяющимися переменными Охлаждение тела
- •Вопрос 17
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Уравнения с правой частью специального вида
Вопрос 12
Тройной интеграл и
его свойства. Пусть
![]() -
ограниченная замкнутая пространственная
область, границей которой является
кусочно-гладкая поверхность, и пусть
функция
-
ограниченная замкнутая пространственная
область, границей которой является
кусочно-гладкая поверхность, и пусть
функция
![]() определена
и ограничена в
.
Посредством сетки кусочно-гладких
поверхностей разобьем
на
конечное число элементарных областей
определена
и ограничена в
.
Посредством сетки кусочно-гладких
поверхностей разобьем
на
конечное число элементарных областей
![]() с
объемами
с
объемами
![]() (разбиение
).
Пусть
.
наибольший из диаметров областей
(разбиение
).
Пусть
.
наибольший из диаметров областей
![]() ,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
![]() .
Число
.
Число
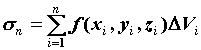 ставится
в соответствие каждому разбиению
и
каждому выбору точек
и
называется интегральной суммой. Если
существует
и
он не зависит от выбора разбиения
и
точек,
то
функция называется интегрируемой по
Риману в области
,
а сам предел называется тройным интегралом
от функции
по
области
и
обозначается
ставится
в соответствие каждому разбиению
и
каждому выбору точек
и
называется интегральной суммой. Если
существует
и
он не зависит от выбора разбиения
и
точек,
то
функция называется интегрируемой по
Риману в области
,
а сам предел называется тройным интегралом
от функции
по
области
и
обозначается
![]() .
Свойства тройных интегралов такие же,
как и у двойных интегралов.
.
Свойства тройных интегралов такие же,
как и у двойных интегралов.
![]()
Вычисление тройного
интеграла в декартовых координатах.
Пусть
является
цилиндрическим телом, проекция которого
на плоскость
есть
область
и
которое ограничено снизу поверхностью
![]() ,
а сверху v поверхностью
,
а сверху v поверхностью
![]() ,
где
,
где
![]() -
непрерывные функции в . Тогда
-
непрерывные функции в . Тогда
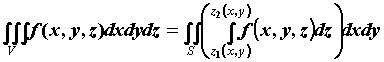 ,
то есть интегрированием по z тройной
интеграл сводится к двойному интегралу
по области
.
Для областей более сложной формы
вычисление двойных и тройных интегралов
производится разбиением областей на
конечное число простых областей с уже
рассмотренными свойствами.
,
то есть интегрированием по z тройной
интеграл сводится к двойному интегралу
по области
.
Для областей более сложной формы
вычисление двойных и тройных интегралов
производится разбиением областей на
конечное число простых областей с уже
рассмотренными свойствами.
Вычисление тройных интегралов с помощью повторного интегрирования.
1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.
Пусть сначала T = [a, b; c, d; e, f] - прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда
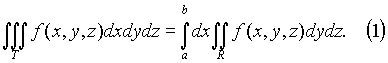
Заменяя в (1) двойной интеграл повторным, получим
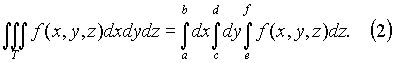
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Если первые два интеграла в (2) объединить в двойной, то будем иметь
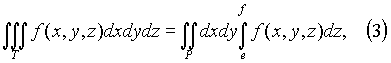
где P = [a, b; c, d] - проекция параллелепипеда T на плоскость xy.
Заметим, что в этих случаях можно менять роли переменных.
2. Пусть
область T
заключена между плоскостями x
= a и x = b,
причём каждое сечение области T
плоскостью
![]() представляет
собой квадрируемую фигуру G(x)(рис.
1). Тогда
представляет
собой квадрируемую фигуру G(x)(рис.
1). Тогда
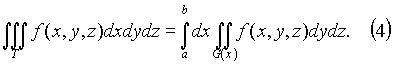
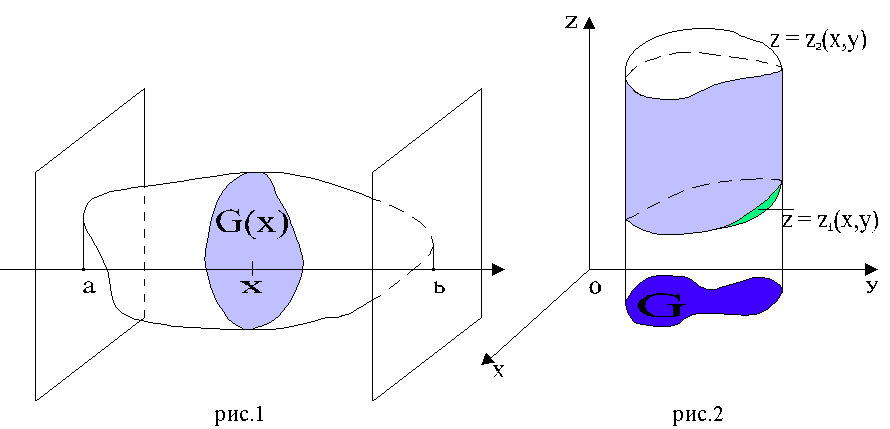
3. Пусть теперь тело T представляет собой "цилиндрический брус", ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z1(x, y) и z2(x, y) - непрерывны в G. Тогда
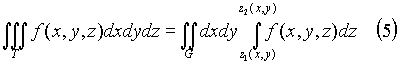
Если
G
= {(x, y): a
![]() x
b,
y1(x)
y
y2(x)},
то
x
b,
y1(x)
y
y2(x)},
то
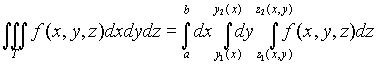
Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.
II.
Замена переменных в тройном интеграле
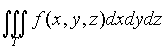 состоит
в переходе от переменных x,
y, z к новым
переменным u,
v, w по формулам
состоит
в переходе от переменных x,
y, z к новым
переменным u,
v, w по формулам
![]()
Если выполняются условия
1?. Отображение (6) взаимно однозначно;
2?. Функции в (6)
непрерывно - дифференцируемы в области
![]()
3?. Якобиан отображения

то имеет место формула
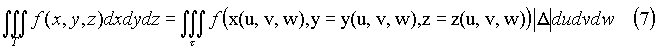
Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.
1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
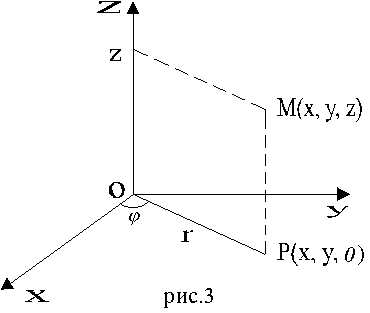
Пусть
M(x, y, z)
- произвольная точка в пространстве
xyz,
P
- проекция точки M
на плоскость xy.
Точка M
однозначно определяется тройкой чисел
![]() -
полярные координаты точки P,
z
- аппликата точки M.
Формулы, связывающие их с декартовыми,
имеют вид
-
полярные координаты точки P,
z
- аппликата точки M.
Формулы, связывающие их с декартовыми,
имеют вид
![]()
![]()
Якобиан
отображения (8)
![]()
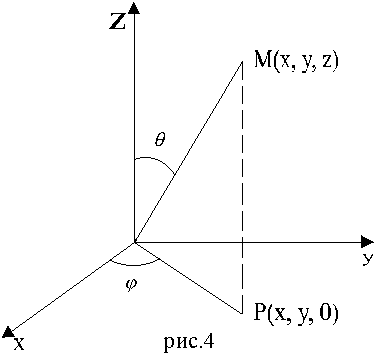
2.
Сферические координаты. Пусть
M(x, y)
- произвольная точка в пространстве
xyz,
P
- проекция точки M
на плоскость xy.
Точка M
однозначно задаётся тройкой чисел
![]() ,
где r
- расстояние точки M
до точки 0,
,
где r
- расстояние точки M
до точки 0,
![]() -
угол между лучами OM
и OZ,
-
угол между лучами OM
и OZ,
![]() -
полярный угол точки P
на плоскости xy.
Тройка чисел
называется
сферическими координатами точки M.
-
полярный угол точки P
на плоскости xy.
Тройка чисел
называется
сферическими координатами точки M.
Они связаны с прямоугольными формулами
![]()
![]()
Якобиан
отображения
![]() .
Иногда используются обобщённые
сферические координаты.
.
Иногда используются обобщённые
сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
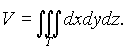
Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
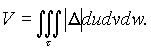
Пусть T
- материальное тело (кубируемая область)
с плотностью
![]()
Тогда
![]() -
масса тела.
-
масса тела.
