
- •Вопрос1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Вопрос 5
- •Вопрос 6
- •Связь с градиентом
- •Вопрос 7
- •Тейлора формула
- •Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •Вопрос 8
- •Описание метода
- •Вопрос 9
- •Вопрос 10 Криволинейный интеграл
- •Вопрос 11
- •Вопрос 12
- •Вопрос 13
- •Поверхностный интеграл первого рода Определение
- •Параметрическая форма
- •Свойства
- •Поверхностный интеграл второго рода Определение
- •Связь между поверхностными интегралами второго и первого рода
- •Свойства
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16 Примеры физических задач, приводящих к уравнениям с разделяющимися переменными Охлаждение тела
- •Вопрос 17
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Уравнения с правой частью специального вида
Вопрос 10 Криволинейный интеграл
Криволинейный интеграл, интеграл, взятый вдоль какой-либо кривой на плоскости или в пространстве. Различают К. и. 1-го и 2-го типов. К. и. 1-го типа возникает, например, при рассмотрении задачи о вычислении массы кривой переменной плотности; он обозначается через
![]() ,
,
где С — заданная кривая, ds — дифференциал её дуги, a f (P) — функция точки на кривой, и представляет собой предел соответствующих интегральных сумм (см. Интеграл). В случае плоской кривой С, заданной уравнением у = у (х), К. и. 1-го типа сводится к обыкновенному интегралу по формуле:
![]() .
.
К. и. 2-го типа возникает, например, при рассмотрении задачи о работе силового поля; в случае плоской кривой С он имеет вид:
![]()
и является также пределом соответствующих интегральных сумм. К. и. 2-го типа сводится к обыкновенному интегралу по формуле:
![]() ,
,
где х = x (t), у = у (t) (a £ t £b) — уравнения кривой С в параметрической форме, и к К. и. 1-го типа по формуле:
![]() ;
;
здесь a — угол между осью Ox и касательной к кривой, направленной в сторону возрастания дуги.
Криволинейный интеграл введен для определения характеристик векторного поля, т.е он имеет именно физический смысл. У него нет наглядного геометрического смысла, как у определенного интеграла.
Криволинейный интеграл и его механический смысл.
X=x(t)Y=y(t) дифференцируемые.V(дуга) AoAnT=α Ao(x(α); y(α))T=β An(x(β); y(β))X=R costY=RsintПусть в каждой точке с координатами(х;у) действует сила F которая зависитот этой точки и имеет х-вую и у-вуюсоставляющую F(x;y)=P(x;y)i+Q(x;y)jA работа-?Разобъем дугу на н частей.T принадлежит [α;β]V AoA1,A1A2….An-1,AnЗначит что на [α;β][to;t1]=t*1[tn-1;tn]=t*nв каждой из полученных частейвыбираем точку.A*I (x(t*I);y(t*I))Составим суммуΣF*(x(t*I);y(t*I)) Ai-1.AiРассмотрим предел последовательноститаких сумм когда max [Ai-1;Ai] nстремится к бесконечLimΣF*(x(t*I);y(t*I)) Ai-1.AiЕсли этот предел существует,конечен ине зависит от способа деления дуги на nчастей и от выбора точек A*I внутрикаждой части то этот предел называетсякриволинейным интегралом по дугеAoAn от выражения ∫ F(x;y)dx+Q(x;y)dyF,Q – силыГеометрический смысл.Fdr, dr-перемещениеСкалярное произведение F(работа- это есть сила на перемещение)A=∫Fdr Это работа перемещение материальнойточки вдоль дуги AoAn под действиемсилы имеющей составляющей поля скоординатами P(x;y) Q(x;y)∫P(x;y)dx+Q(x;y)dy
Вопрос 11
Двойной интеграл в декартовых
координатах. Пусть
![]() ограниченная
замкнутая область плоскости
ограниченная
замкнутая область плоскости
![]() с
кусочно-гладкой границей и пусть функция
с
кусочно-гладкой границей и пусть функция
![]() определена
и ограничена на
.
Посредством сетки кусочно-гладких
кривых разобьем
на
конечное число элементарных областей
определена
и ограничена на
.
Посредством сетки кусочно-гладких
кривых разобьем
на
конечное число элементарных областей
![]() с
площадями
с
площадями
![]() (разбиение
(разбиение
![]() ).
Пусть
).
Пусть
![]() -
наибольший из диаметров областей
-
наибольший из диаметров областей
![]() ,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
![]() .
Число
.
Число
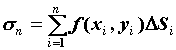 называется
интегральной суммой и ставится в
соответствие каждому разбиению
и
каждому выбору точек
называется
интегральной суммой и ставится в
соответствие каждому разбиению
и
каждому выбору точек
![]() .
Если существует
.
Если существует
![]() и
он не зависит от выбора разбиения
и
точек
,
то функция называется интегрируемой
по Риману в области
,
а сам предел называется двойным интегралом
от функции
по
области
и
обозначается
и
он не зависит от выбора разбиения
и
точек
,
то функция называется интегрируемой
по Риману в области
,
а сам предел называется двойным интегралом
от функции
по
области
и
обозначается
![]() или
или
![]() .
Двойной интеграл существует, если
непрерывна
на
.
Допустимы точки разрыва первого рода,
лежащие на конечном числе гладких кривых
в
.
.
Двойной интеграл существует, если
непрерывна
на
.
Допустимы точки разрыва первого рода,
лежащие на конечном числе гладких кривых
в
.
Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла:
Линейность:
![]() .
Аддитивность:
.
Аддитивность:
![]() ,
если S1 и S2 две области без общих внутренних
точек.
,
если S1 и S2 две области без общих внутренних
точек.
Если для каждой точки
![]() выполнено
неравенство
выполнено
неравенство
![]() ,
то
,
то
![]() .
.
Если
интегрируема
на
,
то функция
![]() также интегрируема, причем
.
также интегрируема, причем
.
Если
![]() и
и
![]() наименьшее
и наибольшее значения функции
в
области, а ее
наименьшее
и наибольшее значения функции
в
области, а ее
![]() площадь,
то
площадь,
то
![]() .
.
Теорема о среднем значении:
если
непрерывна
в связной области
,
то существует, по крайней мере, одна
точка
![]() такая,
что
такая,
что
![]() .
.
Вычисление двойного интеграла.
Если
![]() ,
где -
,
где -
![]() непрерывные на
непрерывные на
![]() функции,
то двойной интеграл может быть вычислен
двумя последовательными интегрированиями:
функции,
то двойной интеграл может быть вычислен
двумя последовательными интегрированиями:
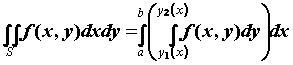 .
Аналогично, если
.
Аналогично, если
![]() ,
то
,
то
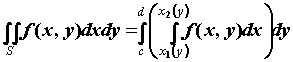 .
.
Пусть в некоторой области D на координатной плоскости XOY определена функция двух переменных z = f (x, y). Предполагается, что граница области D состоит из конечного числа кривых, заданных уравнениями вида y = f (x) или x = φ (y), где f (x) и φ (y) – непрерывные функции.
Разобьем область D на бесконечно малые ячейки прямыми, параллельными координатным осям.
В каждой ячейке выберем точку Ci,j(xi, yj).
Вычислим значения f (xi, yj) функции в этой точке.
Эти значения f (xi, yj) умножим на площади ячеек, из которых бралась точка: f (xi, yj)·Δ xi·Δ yj.
Все эти произведения сложим:
![]() .
.
Полученная сумма называется двойной интегральной суммой.
Назовем диаметром d(D) области D наибольшее расстояние между точками этой области. Обозначим через λ наибольший из диаметров частичных областей Di
![]() .
.
О п р е д е л е н и е. Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит от способа разбиения области D, от способа выбора точек Ci,j (xi, yj) внутри каждой ячейки
![]() .
.
В этом случае функция f (x, y) называется подынтегральной, D — областью интегрирования, x и y — переменными интегрирования, ds (или dx·dy) – элементом площади. Мы предполагаем, что функция f (x, y) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т.е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате
{ (x, y) | 0 ≤ x ≤ 1; 0 ≤ y ≤ 1}
следующим образом:
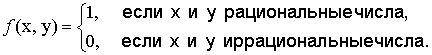
Т е о р е м а 1. Функция f (x, y), непрерывная в замкнутой ограниченной области D, интегрируема в этой области. Т е о р е м а 2. Функция f (x, y),ограниченная в замкнутой ограниченной области D и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида y = ψ(x) или x = φ (y), интегрируема в этой области.
Геометрический смысл двойного интеграла
Пусть тело P в пространстве ограниченно сверху графиком непрерывной и неотрицательной функции z = f(x, y), определенной в области D, цилиндрической поверхностью, направляющей которой служит граница области D, а образующие параллельны оси Oz, и областью D, лежащей в плоскости Oxy. Тело такого вида называют криволинейным цилиндром (цилиндроидом).
Вычисление площади плоской фигуры двойным интегралом
Если положить f (x, y) = 1 всюду в области D, то непосредственно из определения двойного интеграла получим выражение площади s области D в виде двойного интеграла:
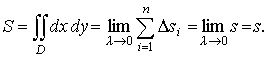
Механический смысл двойного интеграла
Если z = f (x, y)
есть плотность распределения массы по
плоскости, то двойной интеграл есть
масса пластины.
Действительно,
в этом случае f (xi,
yj)·Δ xi·Δ
yj — масса ячейки,
![]() —
приближенная масса пластины. Предел
приближенной массы пластины при условии
измельчения ячеек — масса пластины.
—
приближенная масса пластины. Предел
приближенной массы пластины при условии
измельчения ячеек — масса пластины.
Свойства двойных интегралов
Линейное свойство
![]() .
.
Если функции f (x, y) и g(x, y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и
![]()
Аддитивное свойство по области интегрирования
![]() .
.
Теорема о среднем. Если функция f (x, y) непрерывна в области D, то в этой области найдется такая точка ( ξ; μ), что
![]() ,
,
где s — площадь фигуры D.
