Вопрос 8

Метод множителей Лагранжа, метод нахождения условного экстремума функции  , где  , относительно  ограничений  ,  меняется от единицы до  .

Описание метода

• Составим функцию Лагранжа в виде линейной комбинации функции и функций 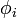, взятыми с коэффициентами, называемыми множителями Лагранжа — ,

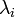, где  .

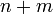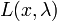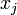• Составим систему из уравнений, приравняв к нулю частные производные функции Лагранжа  по  и  .

• Если полученная система имеет решение относительно параметров 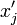 и 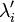 , и градиент функции в точке 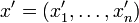не равен нулю, тогда точка x' может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

Пусть на G определена функция . Точка называется точкой условного экстремума функции относительно уравнений связи, если она является точкой обычного экстремума на множестве E (рассматриваются окрестности ).

Метод множителей Лагранжа для решения задачи условного экстремума

Теорема

Пусть  — точка условного экстремума функции при выполнении уравнений связи. Тогда в этой точке градиенты являются линейно зависимыми, то есть но .

Следствие

Если  — точка условного экстремума функции относительно уравнений связи, то такие, что в точке или в координатном виде .

Достаточное условие условного экстремума

Пусть является стационарной точкой функции Лагранжа при . Если  — отрицательно (положительно) определена квадратическая форма переменных при условии , то является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.

Вопрос 9

Задачи, приводящие к кратным интегралам.

К определению двойного интеграла приводит задача вычисления объема прямого цилиндра с плоским основанием, ограниченного сверху некоторой поверхностью. К тройному интегралу приводит задача вычисления массы тела с переменной плотностью. Обе задачи решаются по аналогии с вычислением площади криволинейной трапеции с помощью интегрального исчисления. Так, например, при вычислении объема указанного цилиндра его основание разбивается на множество маленьких областей. Объем каждого цилиндра, построенного на таких областях, близок к объему обычного цилиндра с высотой, равной значению функции, описывающей накрывающую поверхность, в некоторой точке этой частичной области. Объем всего цилиндра близок, таким образом, к сумме объемов всех таких цилиндров. Аналогично решается задача вычисления массы некоторого тела в трехмерном пространстве.

Прежде чем перейти к строгому определению кратных интегралов, вспомним несколько простых понятий, касающихся множества точек пространства .

Определение 1. Точка М называется внутренней точкой множества , если существует окрестность этой точки, целиком состоящая из точек множества D. Точка М называется граничной точкой множества D , если любая ее окрестность содержит как точки множества D , так и точки ему не принадлежащие.

Определение 2. Множество D называется открытым, если оно не содержит ни одной граничной точки и замкнутым, если ему принадлежат все его граничные точки (очевидно, замкнутое множество всегда ограничено).

Определение 3. Множество D называется связным, если две его любые точки можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Областью, по умолчанию, будем называть ограниченное, открытое, связное множество точек.

В противном случае его свойства будут перечислены особо, например: замкнутая область Q.

Замкнутую область часто обозначают следующим образом: .

Определение 4. Диаметром области D называется точная верхняя грань расстояний между двумя ее точками:

Примеры. Отрезок, интервал, шар, эллипс, параллелограмм.

 Задача о вычислении массы неоднородного тела T по известной объемной плотности ρ(M) этого тела естественным образом приводит нас к понятию тройного интеграла.

     Для вычисления массы указанного тела T разобьем его на достаточно малые участки T₁, T₂, ..., T_n. Приближенно можно считать объемную плотность ρ(M) каждого участка T_k постоянной и равной ρ(M_k), где M_k - некоторая точка участка T_k. В таком случае масса каждого участка T_k будет приближенно равна ρ(M_k) · v_k, где v_k - объем участка T_k.

     Приближенное значение массы всего тела T будет равно сумме

Точное значение массы естественно определить как предел указанной суммы при неограниченном уменьшении каждого участка T_k. Этот предел и может быть взят за определение тройного интеграла от функции ρ(M_k) по трехмерной области T.

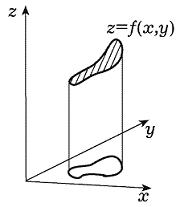
     Совершенно аналогично может быть рассмотрена геометрическая задача о вычислении объема так называемого криводонного цилиндра (т. е. объема изображенного на рисунке тела, лежащего под графиком неотрицательной функции z = f(x, y) в некоторой двумерной области D). Эта задача приводит к понятию двойного интеграла от функции f(x, y) по двумерной области D.

Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью z:

1. Момент инерции равен

 

2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей. 3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс. 4. Момент инерции плоской фигуры относительно оси, перпендикулярной к ее плоскости, равен сумме моментов инерции относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью.