
- •Вопрос1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Вопрос 5
- •Вопрос 6
- •Связь с градиентом
- •Вопрос 7
- •Тейлора формула
- •Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •Вопрос 8
- •Описание метода
- •Вопрос 9
- •Вопрос 10 Криволинейный интеграл
- •Вопрос 11
- •Вопрос 12
- •Вопрос 13
- •Поверхностный интеграл первого рода Определение
- •Параметрическая форма
- •Свойства
- •Поверхностный интеграл второго рода Определение
- •Связь между поверхностными интегралами второго и первого рода
- •Свойства
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16 Примеры физических задач, приводящих к уравнениям с разделяющимися переменными Охлаждение тела
- •Вопрос 17
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Уравнения с правой частью специального вида
Вопрос 7
Производные высших порядков.
Рассмотрим функцию
![]() ,
определенную на некотором промежутке
,
определенную на некотором промежутке
![]() .
Вычислим производную
.
Вычислим производную
![]() ,
которая также является функцией на
.
Производной второго порядка от функции
называется
производная от ее производной:
,
которая также является функцией на
.
Производной второго порядка от функции
называется
производная от ее производной:
![]() .
Аналогично определяют производную
любого порядка:
.
Аналогично определяют производную
любого порядка:
![]() .
.
ПРИМЕР 1. Вычисление производных высших порядков
Дифференциалы высших порядков.
Рассмотрим дифференциал функции
в
произвольной точке промежутка
:
![]() .
Здесь
.
Здесь
![]() -
приращение независимой переменной,
которое является числом и не зависит
от
-
приращение независимой переменной,
которое является числом и не зависит
от
![]() .
Сам же дифференциал есть функция от
,
и можно вычислить дифференциал от этой
функции:
.
Сам же дифференциал есть функция от
,
и можно вычислить дифференциал от этой
функции:
![]() При
При
![]() этот
дифференциал от дифференциала называется
дифференциалом второго порядка и
вычисляется по формуле
этот
дифференциал от дифференциала называется
дифференциалом второго порядка и
вычисляется по формуле
![]() Аналогично
вычисляется дифференциал любого порядка
Аналогично
вычисляется дифференциал любого порядка
![]() .
.
ПРИМЕР 2. Вычисление дифференциалов высших порядков
Понятие инвариантности формы дифференциала.
Рассмотрим дифференциал функции
в
произвольной точке промежутка
:
.
Здесь
-
приращение независимой переменной,
которое является числом и не зависит
от
.
Пусть теперь
![]() -
функция независимого переменного
-
функция независимого переменного
![]() ,
определенная на промежутке
,
определенная на промежутке
![]() .
Тогда
.
Тогда
![]() -
сложная функция переменного
.
Вычислим ее дифференциал, используя
формулу для производной сложной функции:
-
сложная функция переменного
.
Вычислим ее дифференциал, используя
формулу для производной сложной функции:
![]() .
Заметим, что
.
Заметим, что
![]() и
выражение для дифференциала принимает
ту же форму
,
хотя здесь
уже
функция переменного
.
Это свойство дифференциала первого
порядка называется инвариантностью
(т.е. неизменностью) его формы. При
вычислении дифференциала второго
порядка придется учитывать, что
-
функция переменного
.
Поэтому
и
выражение для дифференциала принимает
ту же форму
,
хотя здесь
уже
функция переменного
.
Это свойство дифференциала первого
порядка называется инвариантностью
(т.е. неизменностью) его формы. При
вычислении дифференциала второго
порядка придется учитывать, что
-
функция переменного
.
Поэтому
![]() и
форма второго (а также и всех следующих)
дифференциала неинвариантна.
и
форма второго (а также и всех следующих)
дифференциала неинвариантна.
Тейлора формула
Тейлора формула, формула
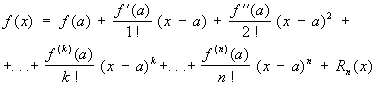
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:
![]() ,
,
где x и x1 — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.
Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
Рассмотрим функцию
![]() ,
где
,
где
![]() --
открытое множество.
--
открытое множество.
Определение 1.
![]() называется
точкой максимума (минимума) функции
называется
точкой максимума (минимума) функции
![]() ,
если
,
если
![]()
Аналогично если выполняется строгое неравенство, точка называется точкой строгого максимума (строгого минимума).
Теорема 1. (необходимое
условие экстремума) Если
![]() --
точка экстремума и существует
--
точка экстремума и существует
![]() ,
то
,
то
![]() .
.
Доказательство. Частную производную
можно представить как производную
функции одной переменной
![]() в
точке
в
точке
![]() .
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной
.
Для этой функции точка
также
является точкой экстремума. Тогда, по
необходимому условию экстремума функции
одной переменной
![]() .
.
![]()
Определение 2.
--
стационарная точка функции
,
если
--
дифференцируема в этой точке и
![]() ,
или
--
не дифференцируема в этой точке.
,
или
--
не дифференцируема в этой точке.
Замечание 1. Квадратичная
форма -- многочлен вида
![]() ,
,
![]() --
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена, если
--
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена, если
![]() положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
Теорема 2. (достаточное
условие экстремума) Если
дважды
дифференцируема в стационарной точке
,
то
--
точка минимума (максимума), если
квадратичная форма
![]() положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
Доказательство. По формуле
Тейлора приращение функции в точке
можно
записать в виде
![]() ,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде
,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде
![]() ,
причем
,
причем
![]() при
при
![]() .
Заметим, что новые переменные
.
Заметим, что новые переменные
![]() изменяются
на единичной сфере, т.к.
изменяются
на единичной сфере, т.к.
![]() .
Кроме того, квадратичная форма
.
Кроме того, квадратичная форма
![]() непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его
непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его
![]() .
Пусть форма положительно определена.
Тогда
.
Пусть форма положительно определена.
Тогда
![]() .
Теперь благодаря тому, что
при
можно
подобрать такое
.
Теперь благодаря тому, что
при
можно
подобрать такое
![]() ,
что при
,
что при
![]() выполнено
выполнено
![]() ,
тогда выполнено
,
тогда выполнено
![]() в
этой окрестности. Что и означает, что
--
точка минимума. Для точки максимума
доказательство аналогично.
в
этой окрестности. Что и означает, что
--
точка минимума. Для точки максимума
доказательство аналогично.
