Вопрос 20
Дифференциальное уравнение называется линейным, если неизвестная функция и все ее производные входят в уравнение линейно:
|
Если f (x) тождественно равна нулю, то уравнение называется однородным; в противном случае оно называется неоднородным.
Принцип
суперпозиции. Если
и
–
решения однородного уравнения
то
y (x) = α1 y1 (x) + α2 y2 (x) |
при любых постоянных α1 и α2 является решением однородного уравнения.
Если
и
–
решения неоднородного уравнения
то
их разность
y (x) = y1 (x) – y2 (x) |
есть решение
однородного уравнения
Всякое решение
неоднородного уравнения
есть
сумма частного решения этого неоднородного
уравнения и общего решения соответствующего
ему однородного уравнения
Уравнение вида
|
где a1, …, an – некоторые постоянные, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Всякое решение однородного уравнения первого порядка
|
имеет вид
|
где C – постоянная.
Уравнение вида
|
где Pm (x) – многочлен степени m, μ – постоянная, имеет частное решение вида
|
если μ ≠ λ, и вида
|
если μ = λ. Здесь Qm (x) – многочлен степени m.
В общем случае
у однородного линейного дифференциального
уравнения с постоянными коэффициентами
имеется
так называемое характеристическое
уравнение
Корни
этого уравнения – характеристические
числа – являются показателями степеней
слагаемых, входящих в решение. Если
среди корней уравнения
нет
кратных, то решением однородного
уравнения является функция вида
где
все
–
некоторые константы, зависящие от
начальных условий. Количество слагаемых
в этой функции совпадает со степенью
дифференциального уравнения. Если же,
скажем,
–
корень характеристического уравнения
кратности m, то соответствующее слагаемое
принимает вид
а
общее количество слагаемых, входящих
в решение однородного дифференциального
уравнения уменьшается на m – 1.
Уравнение
|
где ω > 0, называется уравнением гармонических колебаний. Его нетривиальным решением является функция вида
x (t) = C1 cos ωt + C2 sin ωt, |
где C1, C2 – постоянные. Эту функцию можно представить в виде
x (t) = A cos (ωt – φ), |
где
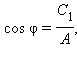
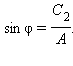
Уравнение
|
сводится к трем случаям:
a2 < ω2:
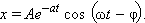
Эта функция не периодическая, но ее максимумы и минимумы повторяются с периодом T = 2π/ω. Величина A e–at называется амплитудой затухающих колебаний. Заметим, что она существенно зависит от времени.
a2 > ω2:
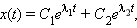
где λ1 и λ2 – постоянные:
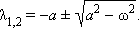
Функция x(t) – непериодична, это – апериодический процесс.
теме |
Справочники, руководства |
Решение задач в онлайн режиме |