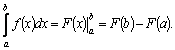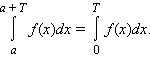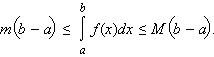Вопрос1

Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

• Если функция интегрируема на [a; b], то она интегрируема на любом отрезке

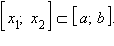
• Для любых a, b и c

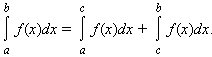
• Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

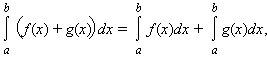
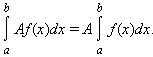
• Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.

• Если f (x) – периодическая функция с периодом T, то для любого a

Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

• Если f (x) ≥ g (x), то

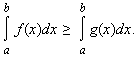
• В частности, если f (x) ≥ 0, то

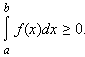
• Если f (x) ≥ 0 для любого 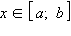 и существует такое, что 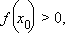 причем f (x) непрерывна в 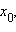 то

• |f (x)| интегрируема на [a; b], причем

• Если на отрезке [a; b]  m ≤ f (x) ≤ M, то

Пусть определена на . Разобьём на части с несколькими произвольными точками Тогда говорят, что произведено разбиение отрезка Далее выберем произв. точку , ,

Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю , если он существует независимо от разбиения и выбора точек , т.е.

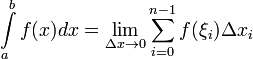
Если в определенном интеграле 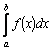изменять верхний предел b, то будет меняться и значение интеграла, то есть интеграл будет функцией верхнего предела.

Обозначим верхний предел x, а переменную интегрирования, чтобы не смешивать ее с верхним пределом, обозначим t. Таким образом, интеграл с переменным верхним пределом является функцией от x: .

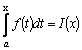Имеет место теорема: производная интеграла с переменным верхним пределом от непрерывной функции равна подынтегральной функции, в которой переменная интегрирования заменена верхним пределом:

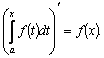
Доказательство. По определению производной

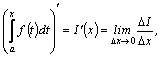где [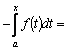первый интеграл представим в виде суммы двух интегралов, пользуясь свойством аддитивности]= [по теореме о среднем]= где

Тогда следует из определения непрерывной функции, т.к. при . Таким образом,

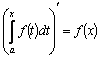
Это значит, что интеграл с переменным верхним пределом является первообразной для функции .

Формула Ньютона–Лейбница

Теорема. Если – какая–либо первообразная для непрерывной функции , то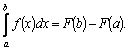

Доказательство. Пусть –некоторая первообразная функции . Но – также первообразная для , а любые две первообразные данной функции отличаются на постоянную, то есть можно записать:

(4)

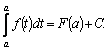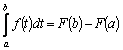Это равенство справедливо для любых . Положим : Но , поэтому , . Полагая в (4) x=b и подставляя значение C, получим Переобозначив переменную интегрирования , получим формулу Ньютона – Лейбница:

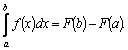
При вычислении определенных интегралов будем записывать: