28. Определите p-значение статистического критерия. Каким образом находится p-значение, если известно распределение статистики критерия ? Рассмотрите случай критической области вида

Определение: Для фиксированной реализации выборки Р-значением статистического критерия называется такое число PV( ), что PV( )≥α для любого уровня значимости α, при котором гипотеза Н0 принимается, и PV( )≤альфа, для любого уровня значимости альфа, при котором гипотеза Н0 отвергается.

Предположим, что Р-значение PV( ) уже каким-либо способом найдено. Тогда решение о принятии (отклонении) Н0 для заданного α осуществляется на основе следующего простого правила: если PV( ) <α, гипотеза Н0 отвергается, а если PV( )> α гипотеза Н0 принимается.

Рассмотрим отдельно случай PV( ) =α. Как правило, критическую область можно представить в виде

Где с(α)-непрерывная убывающая функция. Как нетрудно видеть, в этом случае и для PV( ) =альфа имеет место равенство

Означающее, что Н0 принимается. Отсюда :

Действительно, при любом уровне значимости α имеем

Аналогично, ,где с(α) – непрерывная возрастающая функция, Р-значение удовлетворяет соотношению

29. В чем состоит метод наименьших квадратов (мнк)? Используя матричную запись, укажите явный вид (приближенного) решения системы линейных уравнений по мнк. В каком случае мнк-решение не существует?

Пусть имеется Система из 3-х уравнений:

a₁₁х₁+ a₁₂х₂=b₁

a₂₁х₂+ a₂₂х₂=b₂ (1)

a₃₁х₃+ a₃₂х₂=b₃

Система, в общем говоря несовместн. После подстановки в нее произвольной пары чисел х₁ и х₂ одно или несколько уравнений будут нарушены.Отклонением (или невязкой) i-ого уравнения называются разность между его левой и правой частями.

e_i= a_i1х₁₁+ ai₂х₂-b_i

Сумма квадратов отклонений во всех уравнениях далее обозначается

S(х₁, х₂)= е₁^2 + е₂^2 + е₃^2 (измеряет качество решения)

O: Метод наименьших квадратов – метод приближенных решений СЛУ состоит в том, что ищется приближенное решение с наименьшей суммой квадратов ошибок. (1) сводится к (2).

S(х1,х1)→min (2)

Явный вид решения системы лин. уравнений по МНК

Формула задает МНК-решение записанной в матричном виде линейной системы с произвольным числом неизвестных и уравнений. Единственное ограничение состоит в том, чтобы столбцы матрица А были линейно независимы, т.е. при линейсной зависимости столбцов матрицы А решения не существует. Несложно доказывается например, что при условии обратная матрица существует, что обеспечивает существование и единственность решения системы.

30. Используя метод наименьших квадратов, найдите коэффициенты α и β, удовлетворяющие соотношениям: α+βx₁ ≈ y₁, α+βx₂ ≈ y₂, ...,α+βxn ≈ yn.

Предположим, что на плоскости задано n точек (х1,y1),…,(xn,yn) и необходимо подобрать прямую , проходящую как можно ближе к этим точкам. Если бы все точки лежали на прямой, то коэффициенты были бы решением системы:

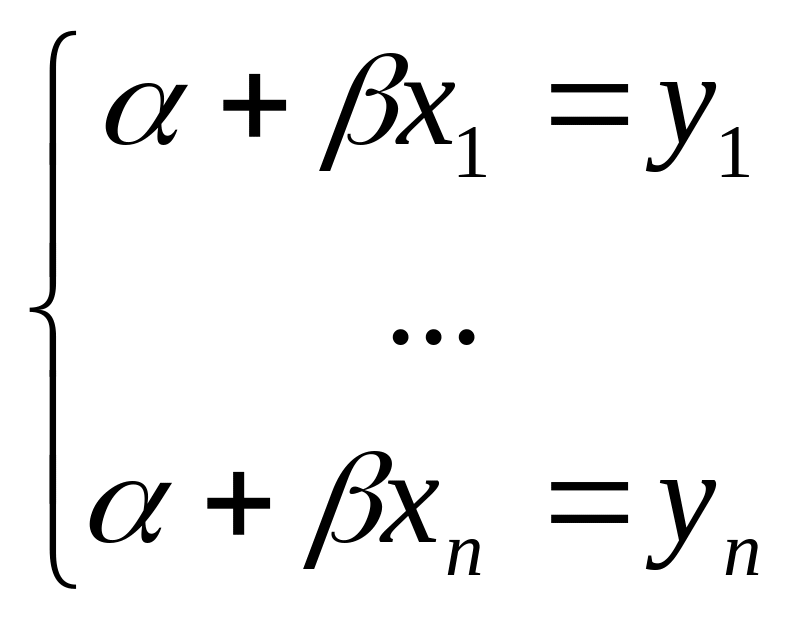
На самом деле точки обычно не лежат на одной прямой и система является несовместной. Тем не менее, коэффициенты α иβискомой функции легко находятся как МНК-решения системы.

,

где ,

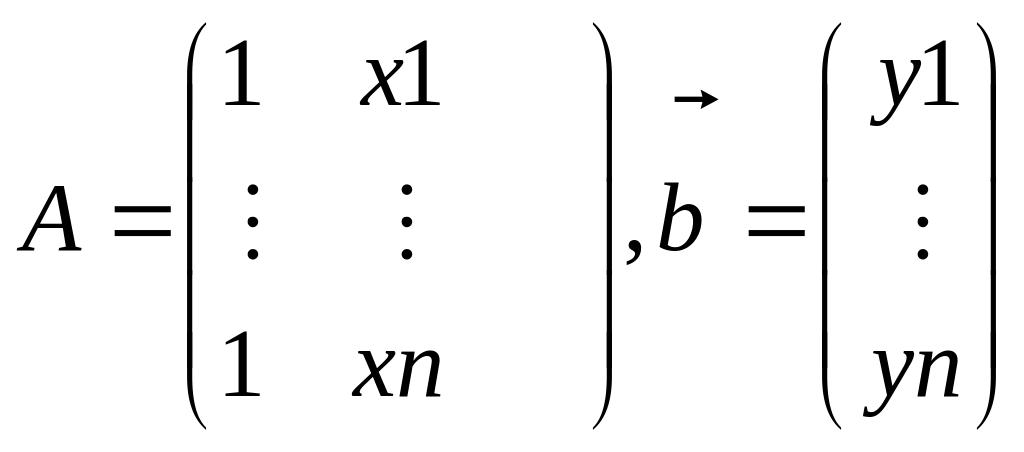и применяя формулу , получим

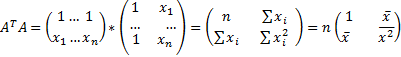
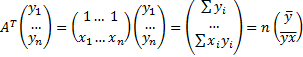
Исходные данные x1,…,xn; y1,…,yn далее интерпретируются как значения некоторых признаков Х, Y в совокупности ={1,..,n}, где xi=X(i), yi=Y(i),

, где – выборочная дисперсия