
- •Запишите формулы для математического ожидания и дисперсии выборочной доли в случае повторной (бесповторной) выборки. Поясните все используемые обозначения.
- •Сформулируйте определение выборки из распределения. Как в этом случае определяются: выборочное среднее, выборочные начальные и центральные моменты, выборочная функция распределения?
- •Докажите формулы для математического ожидания и дисперсии выборочного среднего в случае повторной выборки.
- •Выведите формулу для дисперсии выборочного среднего бесповторной выборки.
- •Что такое точечная статистическая оценка? Какие оценки называются несмещенными, эффективными, состоятельными? Приведите пример эффективной оценки.
- •Запишите формулу для несмещенной оценки начального момента произвольного порядка. Докажите несмещенность.
- •Сформулируйте теорему Слуцкого и на ее основе докажите теорему о состоятельных оценках центральных моментов.
- •Сформулируйте и докажите теорему о состоятельности оценок метода моментов.
- •Сформулируйте определения распределений χ², Стьюдента и Фишера. Какие из этих распределений являются симметричными?
- •Что называется интервальной оценкой параметра распределения? Какие оценки называются симметричными по вероятности? Определите понятия: доверительная вероятность и точность оценки.
- •Пояснив используемые символы, запишите (1–α)-доверительный интервал (симметричный по вероятности) для дисперсии при известном математическом ожидании. В каких случаях применима данная формула?
- •Пояснив используемые символы, запишите (1–α)-доверительный интервал (симметричный по вероятности) для дисперсии при неизвестном математическом ожидании. В каких случаях применима данная формула?
- •Запишите приближенный (1–α)-доверительный интервал для генеральной доли признака в случае выборки большого объема n (n→∞). Поясните все используемые символы.
- •Пояснив используемые символы, запишите (1–α)-доверительный (симметричный по вероятности) интервал предсказания. Для каких генеральных распределений применима данная формула?
- •Опишите общую схему проверки статистических гипотез. Определите понятия: критическая область, уровень значимости, мощность критерия. Какие гипотезы называются простыми (сложными)?
- •Определите отношение правдоподобия для дискретных и абсолютно непрерывных распределений. Сформулируйте теорему (лемму) Неймана – Пирсона и приведите пример наиболее мощного критерия.
- •Для проверки каких гипотез применяется критерий Колмогорова? Каким образом находится значение статистики данного критерия?
- •Определите p-значение статистического критерия. Каким образом находится p-значение, если известно распределение статистики критерия ? Рассмотрите случай критической области вида
- •В чем состоит метод наименьших квадратов (мнк)? Используя матричную запись, укажите явный вид (приближенного) решения системы линейных уравнений по мнк. В каком случае мнк-решение не существует?
Для проверки каких гипотез применяется критерий Колмогорова? Каким образом находится значение статистики данного критерия?
Его применяют для проверки гипотезы о совпадении истинной функции распределения с некоторой гипотетической функцией распределения. Критерий Колмогорова применяется при n≥20
Для любого
![]() число компонент вектора
число компонент вектора
![]() ,
которые меньше
,
которые меньше![]() ,
обозначим
,
обозначим
![]() .
Для случайного вектора
.
Для случайного вектора
![]() обозначение
обозначение
![]() имеет тот же смысл, но при этом
является дискретной случайной величиной
с возможными значениями 0,1,…,n. Пусть
имеет тот же смысл, но при этом
является дискретной случайной величиной
с возможными значениями 0,1,…,n. Пусть
![]() -реализация случайной выборки
-реализация случайной выборки
![]() объема
n из некоторого распределения с функцией
объема
n из некоторого распределения с функцией
![]() .
Эмпирическую функцию распределения,
соответствующую выборке
.
Эмпирическую функцию распределения,
соответствующую выборке
![]() ,
можно записать в виде
,
можно записать в виде
![]()
Оценка функции по случайной выборке записывается аналогично:
![]()
Расстояние между
функциями
![]() (эмпирическая функция) и
(эмпирическая функция) и
![]() (теоретическая
функция) определяется формулой
(теоретическая
функция) определяется формулой
![]()
![]()
Для функции
![]() расстояние
расстояние
![]() - это простое число, тогда как для
- это простое число, тогда как для
![]() расстояние
является случайной величиной, принимающей
значения на отрезке [0,1].
расстояние
является случайной величиной, принимающей
значения на отрезке [0,1].
Теорема:В случае
непрерывной функции F(x) при любом
неотрицательном
![]() существует предел:
существует предел:
![]() где
где
![]()
Вследствие этого критерий согласия с критической областью
![]() где
где
![]() -
корень уравнения
-
корень уравнения
![]() ,
имеет при
,
имеет при
![]() уровень значимости, стремящийся к
.
То есть
- асимптотический уровень значимости.
Именно этот критерий и называется
критерием Колмогорова.
уровень значимости, стремящийся к
.
То есть
- асимптотический уровень значимости.
Именно этот критерий и называется
критерием Колмогорова.
На практике при вычислении максимального абсолютного отклонения теоретической функции от эмпирической функции применяется следующая формула:
![]() где
где
![]() -i-ый
член вариационного ряда
-i-ый
член вариационного ряда
![]()
Итак, схема
применения критерия А. Н. Колмогорова
следующая: строятся эмпирическая функция
распределения
и предполагаемая теоретическая функция
распределения
,
определяется
![]() - максимум модуля разности между ними.
Далее определяется величина
- максимум модуля разности между ними.
Далее определяется величина
![]() и по табличным значениям находится
вероятность того, что, если случайная
величина действительно распределена
по закону
,
за счет чисто случайных причин максимальное
расхождение между
и
будет не меньше, чем фактически
наблюденное. Если вероятность весьма
мала, гипотезу следует отвергнуть как
неправдоподобную; при сравнительно
больших значениях вероятности ее можно
считать совместимой и опытными данными.
и по табличным значениям находится
вероятность того, что, если случайная
величина действительно распределена
по закону
,
за счет чисто случайных причин максимальное
расхождение между
и
будет не меньше, чем фактически
наблюденное. Если вероятность весьма
мала, гипотезу следует отвергнуть как
неправдоподобную; при сравнительно
больших значениях вероятности ее можно
считать совместимой и опытными данными.
Сформулируйте критерий по проверке с заданным уровнем значимости α гипотезы о равенстве нескольких генеральных средних методом дисперсионного анализа. Каким образом находится значение статистики данного критерия?
Пусть
![]() -выборка
объема ni из нормального
распределения с параметрами мю и сигма,
где i=1,…,k.
Предположим, что n=n1+…+nk
случайных величин
-выборка
объема ni из нормального
распределения с параметрами мю и сигма,
где i=1,…,k.
Предположим, что n=n1+…+nk
случайных величин
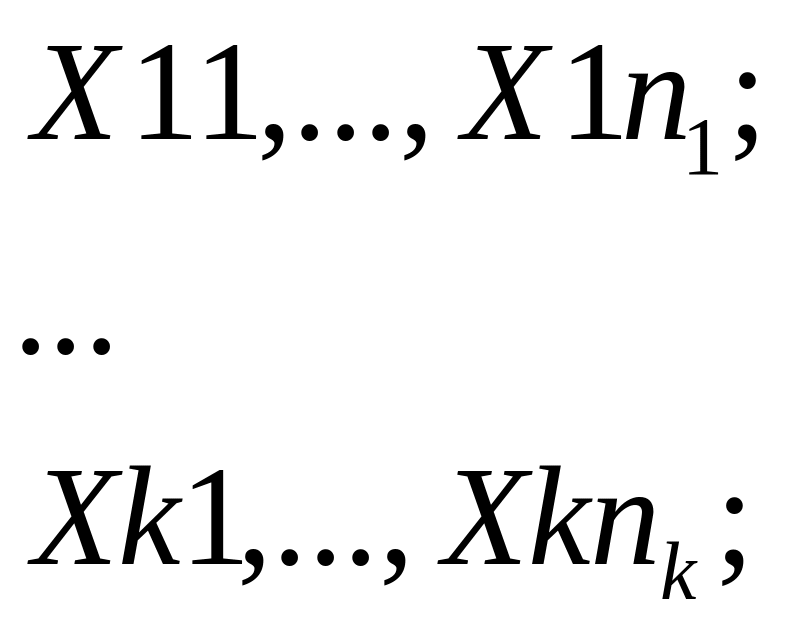
Независимы в
совокупности. Таким образом, выборки
![]() независимы и получены из нормальных
распределений с одинаковой дисперсией
сигма квадрат и, возможно, различными
средними мю1,…,мюк. Гипотеза о равенстве
всех средних одновременно записывается
как Н0: мю1=…=мюк
независимы и получены из нормальных
распределений с одинаковой дисперсией
сигма квадрат и, возможно, различными
средними мю1,…,мюк. Гипотеза о равенстве
всех средних одновременно записывается
как Н0: мю1=…=мюк
А альтернативная гипотеза – как
Н1: (![]()
Заметим, что при верной Н0 выборки являются предположениях может рассматриваться как параметрический аналог рассмотренных ранее непараметрический гипотез однородности.
Рассмотрим объединенную выборку объема n=n1+…+nk:
![]()
Интерпретируя выборки как группы, на которые разбита совокупность , введем обозначения:
![]() -выборочное
среднее в i-ой совокупности
-выборочное
среднее в i-ой совокупности
![]() -выборочная
дисперсия в той же выборке
-выборочная
дисперсия в той же выборке
![]() -выборочное
среднее в объединенной выборке
-выборочное
среднее в объединенной выборке
![]() -средняя
групповая дисперсия
-средняя
групповая дисперсия
![]() -межгрупповая
дисперсия
-межгрупповая
дисперсия
![]() -выборочная
дисперсия признака в объединенной
выборке
-выборочная
дисперсия признака в объединенной
выборке
![]() ,
где первое слагаемое характеризует
среднюю изменчивость признака в каждой
выборке, а второе характеризует разброс
выборочных средних.
,
где первое слагаемое характеризует
среднюю изменчивость признака в каждой
выборке, а второе характеризует разброс
выборочных средних.
Критерий Н0 против Н1 основан на следующей теореме, которую приводим без доказательства
Теорема: Пусть верна гипотеза H0, тогда
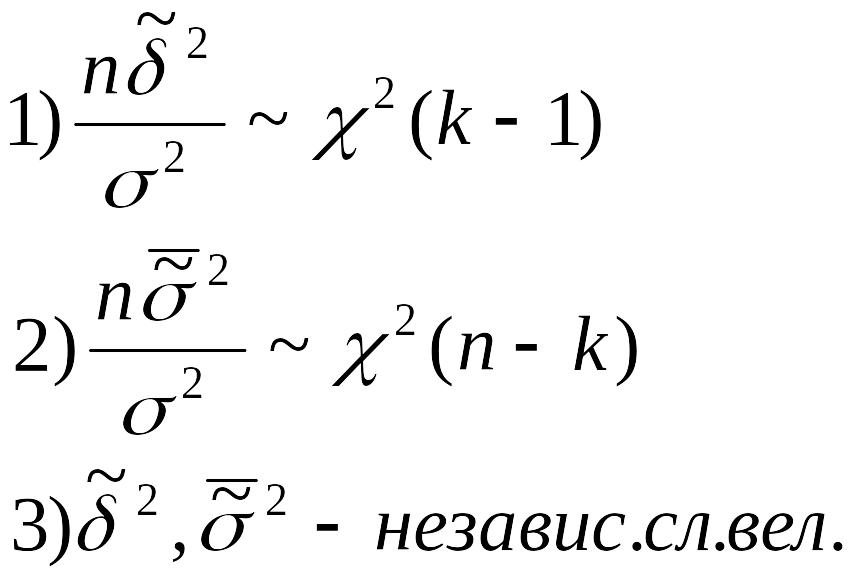
Определим F-отношение

Статистику можно
представить также в виде:
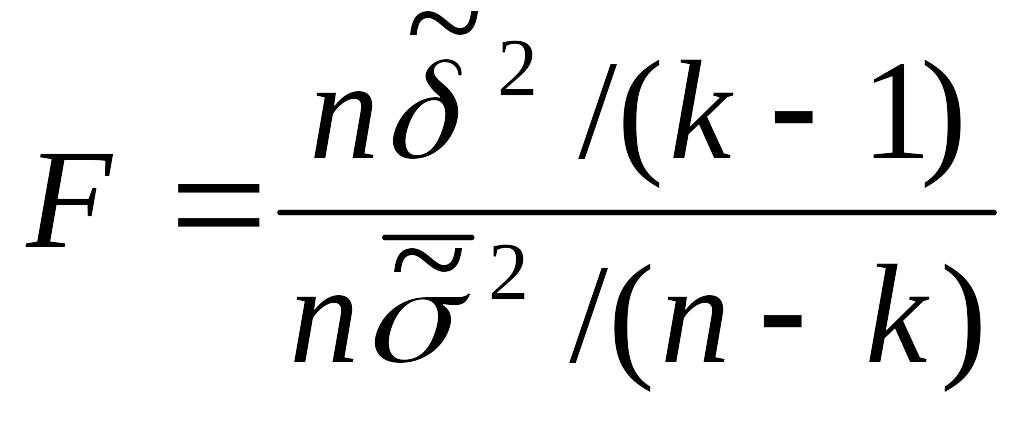
Вывод: для проверки
H0 при уровне значимости α можно
использовать критерий с критической
областью:
![]()
