Опишите общую схему проверки статистических гипотез. Определите понятия: критическая область, уровень значимости, мощность критерия. Какие гипотезы называются простыми (сложными)?
Статистическая гипотеза – любое утверждение о виде параметра генерального распределения. Стат. гипотеза называется параметрической, если она основана на предположении, что генеральное распределение известно с точностью до конечного числа параметров.
Параметрическая
гипотеза называется простой, если
она имеет вид
,
где
-
параметр распределения (возможно
вектор), а
-
некоторое фиксированное значение
параметра. Гипотеза вида
,
где
-
множество, содержащее, по меньшей мере,
2 элемента, называется сложной.
Пусть Н0 и Н1 – взаимоисключающие статистические гипотезы. Гипотезу Н0 назовем основной, а гипотезу Н1 – альтернативной.
Статистическим
критерием с критической областью К
называется правило, в соответствии с
которым гипотеза
,
если выборка (x1,..,xn)принадлежит
К и принимается, если (x1,..,xn)
не принадлежит К. Как правило, критическая
область задается при помощи неравенства:
с,с1,с2-критические
значения, а функция t -
статистика критерия.
Общая схема заключается в проверке принадлежности значения критерия критической области.
Ошибка первого рода : отвергается верная гипотеза Но.
Ошибка второго рода: отвергается верная гипотеза Н1.
Опр: Вероятность ошибки первого рода называется уровнем значимости критерия и обозначается альфа. Вероятность ошибки второго рода обозначается бета, а величина 1-бетта называется мощностью критерия.
Определите отношение правдоподобия для дискретных и абсолютно непрерывных распределений. Сформулируйте теорему (лемму) Неймана – Пирсона и приведите пример наиболее мощного критерия.
Пусть генеральное
распределение имеет строго положительная
плотность
,зависящую
от параметра тетта. H0 и
Н1 – простые гипотезы:
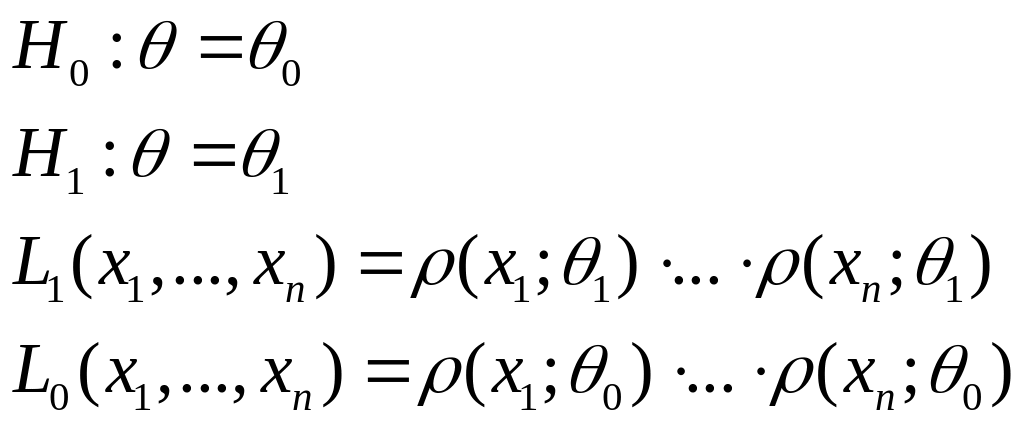
L0, L1- функции правдоподобия, соответствующие гипотезам.
отношением правдоподобия называется отношение
-
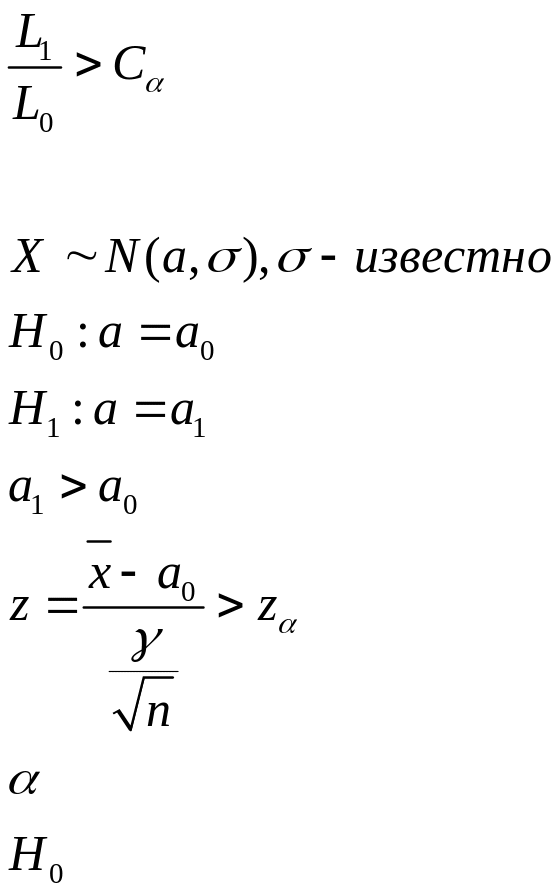отношение правдовобия (1-я строка)
Лемма Немана-Пирсона:
Для любого уровня значимости
существует такая константа
,
что критерия с критической областью:
является наиболее
мощным критерием среди всех статистических
критериев с какой-либо критической
областью К по проверке статистической
гипотезы
против гипотезы
с уровнем значмости альфа
Пример наиболее мощного критерия:
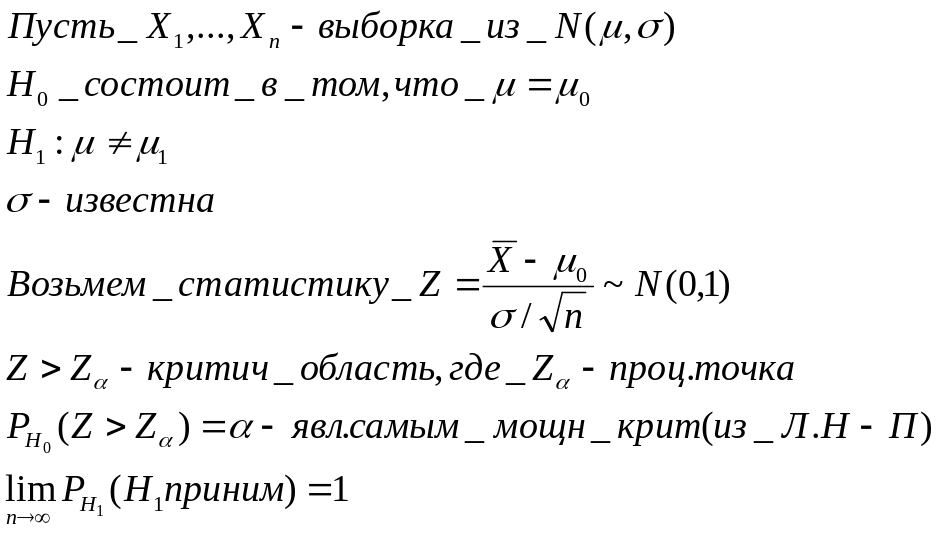
Какие статистические критерии называются критериями согласия? Сформулируйте общую схему по проверке гипотезы о вероятностях событий, образующих полную группу, по критерию Пирсона без оценки неизвестных параметров.
Критерий согласия предназначен для проверки согласованности основной гипотезы Н0 с выборочными данными, однако, в отличии от других критериев, альтернативная гипотеза явным образом не выдвигается.
Производится серия повторных независимых испытаний, wt- элементарный исход испытания с номером t.
Пусть А1,…,Аl – образуют полную группу событий. Исходными данными для критерия хи-квадрат Пирсона является таблица эмпирических частот
Событие |
А1 |
… |
Al |
частота |
|
… |
n |
Если
основная гипотеза верна, согласно
статистическому определению вероятности
-относительная
частота события Аi.
В качестве меры одновременной близости
l
пар чисел (
)
можно принять любую сумму вида
,
в которой ci>0
какие –либо положительные числа.
Заметим, что при верной Но, случайные величины ni распределены по биноминальному закону с параметрами n и pi, вследствие чего npi=Е(ni) называется ожидаемой (теоретической) частотой события Аi.теоретические частоты, ni- кол-во элементарных исходов в группе, l- кол-во групп, pi-заданная вероятность.
Определим l величин:
Где uk,i- i-ая компонента вектора uk, а Xi определяется соотношением
Из
этого следует, что
,
а из ортонормированности базиса
,…,
вытекает,что
суммы квадратов Х1,…,Хl
и Z0,…,Zl-1
совпадают
Нетрудно видеть, что
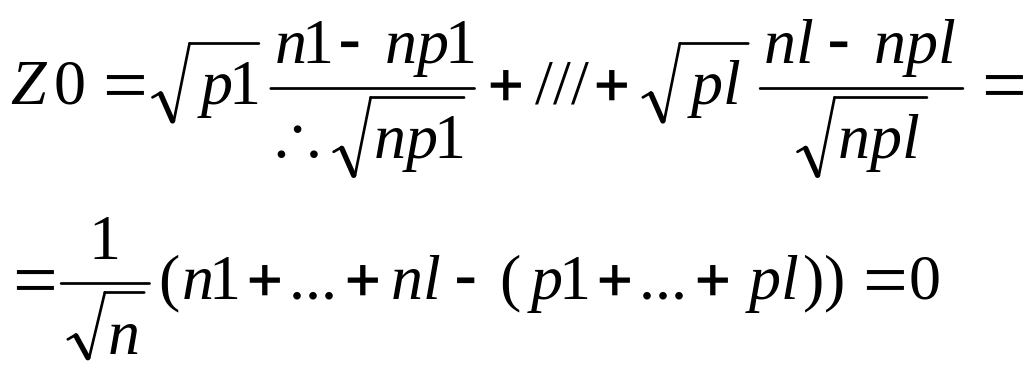
Получаем
Случайный вектор Z имеет нулевое математическое ожидание и единичную ковариационную матрицу. Применяя многомерный аналог центральной предельной теоремы, можно доказать, что при n стремящемся к бесконечности распределение вектора Z стремится к l-1-мерному нормальному распределению. В итоге получаем, что распределение статистики при достаточно большом n близко к распределению хи квадрат с l-1 степенями свободы.
Можно также
доказать, что если гипотеза H0
не верна, то при n стрем.
к бесконечности вероятность
для
любого с, что в конечном счете определяет
достаточно высокую мощность критерия
Пирсона.
В итоге приходим
к выводу, что проверки по эмпирическим
данным справедливости распределения
с асимптотическим уровнем значимости
альфа можно использовать критерий
согласия хи квадрат Пирсона и критической
областью
.
Сформулируйте общую схему статистической проверки гипотезы о виде распределения по критерию Пирсона с оценкой неизвестных параметров. Как частный случай опишите проверку гипотезы о нормальном распределении.
Часто встречаются
ситуации, когда гипотетическая
вероятностная мера Р зависит от одного
или нескольких параметров
,
Р(А)=Р(А;
),
Что приводит к зависимости вероятностей pi от :
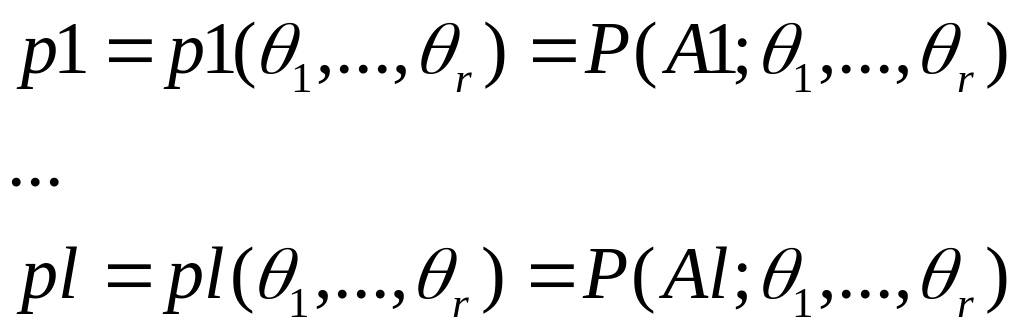
Проверяемая гипотеза Н часто формулируется как утверждение о том, что истинная вероятностная мера Pист совпадает с гипотетической мерой Р при определенных значениях параметров . Тем не менее, фактической проверке подвергается не Н, а вытекающая из Н гипотеза Н0 о том, что распределение частот согласуется с распределением при определенном наборе значений параметров . П любой Н гипотеза Н0 заведомо является параметрической гипотезой.
Предположим, что
-оценки,
полученные методом максимального
правдоподбия по таблице эмпирических
частот
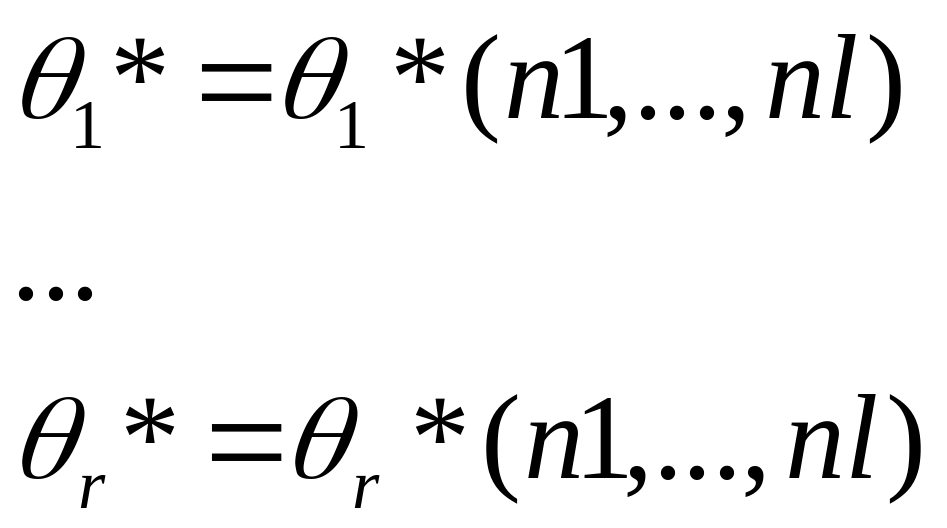
Заменив в
вероятность рi на их оценки
получим
статистику вида
Произведение np*i -ожидаемая частота события Аi
Распределение статистики при n стремящемся к бесконечности стремится к распределения хи квадрат с l-r-1 степенями свободы, в котором число степеней свободы по сравнению с аналогичным предельным распределением уменьшилось на количество оцененных параметров.
Сформулируйте общую схему статистической проверки гипотезы о виде распределения по критерию Пирсона с оценкой неизвестных параметров. Как частный случай опишите проверку гипотезы о нормальном распределении.
Часто встречаются ситуации, когда гипотетическая вероятностная мера Р зависит от одного или нескольких параметров ,
Р(А)=Р(А; ),
Что приводит к зависимости вероятностей pi от :
Проверяемая гипотеза Н часто формулируется как утверждение о том, что истинная вероятностная мера Pист совпадает с гипотетической мерой Р при определенных значениях параметров . Тем не менее, фактической проверке подвергается не Н, а вытекающая из Н гипотеза Н0 о том, что распределение частот согласуется с распределением при определенном наборе значений параметров . П любой Н гипотеза Н0 заведомо является параметрической гипотезой.
Предположим, что -оценки, полученные методом максимального правдоподбия по таблице эмпирических частот
Заменив в вероятность рi на их оценки
получим статистику вида
Произведение np*i -ожидаемая частота события Аi
Распределение статистики при n стремящемся к бесконечности стремится к распределения хи квадрат с l-r-1 степенями свободы, в котором число степеней свободы по сравнению с аналогичным предельным распределением уменьшилось на количество оцененных параметров.