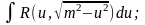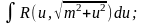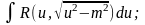- •1.Неопределенный интеграл.
- •2. Первообразные элем.Функций.
- •3.Замена переменных в неопр.Интегралле.
- •4.Интегрирование по частям.
- •5.Интегрирование иррациональных функций.
- •6.Элементарные рац.Функции и интегралы от них.
- •7.Алгоритм
- •8.Интегрирование функций, содержащих радикалы.
- •9.Интегрирование биноминальных дифференциалов.
- •11.Тригонометрическая подстановка.
- •12.Интегр.Функций содержащих показ.Функции
- •13.Определенный интеграл.
- •14.Класс интегрируемых функций
- •15.Определенный интеграл как функция верхнего предела
- •16.Теорема: (Теорема Ньютона – Лейбница)
- •17.Замена переменных.
- •18.Интегрирование по частям.
- •19.Приложения опред. Интеграла
- •1)Площадь плоской фигуры.
- •22.Интеграл Эйлера I рода
- •23.Интеграл Эйлера I I рода
- •24.Функции нескольких переменных
- •25. Непрерывные функции
- •26.Дифференцирование функций нескольких переменных.
- •27.Производная сложной функции
- •28.Частные дифференциалы и дифференциал функции
- •29.Частные производные высших порядков.
- •30.Дифференциалы высших порядков.
- •31.Формула Тейлора
- •32.Градиент.
- •33.Экстремум функции нескольких переменных.
- •34.Теорема. (Достаточные условия экстремума).
- •35.Условный экстремум.
- •36.Билинейная и квадратичная форма
- •38.Второй дифф.Как квадрат.Форма
- •39.Пространства.
- •40.Основные понятия теории дифференциальных уравнений.
- •41.Дифференциальные уравнения первого порядка
- •42.Уравнения с разделяющимися переменными.
- •43.Однородное дифференциальное уравнение первого порядка.
- •44.Уравнения, приводящиеся к однородным. К таким уравнениям относят уравнения вида:
- •45.Линейное уравнение первого порядка
- •46.Уравнение Бернулли
- •47.Уравнение Риккати
- •48.Уравнение в полных дифференциалах и их решение
- •49.Интегральный множитель и его нахождение
- •50.Дифференциального уравнения n-го порядка.
- •51.Диф.Ур.Высшего порядка.Способы пониж.Порядка
- •Уравнения, не содержащие явно искомой функции
- •52.Линейные однородные дифференциальные уравнения с
- •Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
- •54.Метод вариации
- •55.Метод неопределенных коэффициентов.
- •56.Метод Коши
- •57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •58.Нормальные системы обыкновенных дифференциальных уравнений.
- •59.Метод сведения к одному уравнению.
- •60.Метод интегрируемых комбинаций
- •61. Нормальные системы обыкновенных дифференциальных уравнений.
- •62.Фундаментальная система решений как базис линейного пространства решений однородной линейной системы
- •68.Определитель Вронского
- •64.Системы линейных уравнений первого порядка с постоянными коэффициентами: однородные и неоднородные. Структура решения. Алгоритм решения.
- •65.Преобразование Лапласа.
- •66.Интегралл Лапласа и его свойства
- •67.Свойства 1-6 преобразования Лапласа.
- •68.Свойства 7-12 преобразования Лапласа.
- •70.Таблица изображений некоторых функций.
- •72.Интеграл Дюамеля
- •73.Достаточные условия существования оригинала
- •75.Решение уравнений методом Дюамеля.
7.Алгоритм
Интеграл от всякой дробно рациональной функции берёться в конечном виде.
1)f(x)=g(x)+h(x)
g(x)=P(x)-многочлен h(x)=P(x)/Q(x); degP<degQ
Такое разложение можно получить с помощью алгоритма Евклида.
F(x)=P(x)/Q(x) деление в столбик
2)Интеграл g(x) берётся по таблице
3)Для того, чтобы найти интеграл от h(x) разложим знаменатель на множители(не сущ.общего алгоритма решения этой задачи)
Представить Q(x)=…(x-a)k…(x2+px+q)m
4)Методом неопределённых коэфф. P/Q разложить по базису
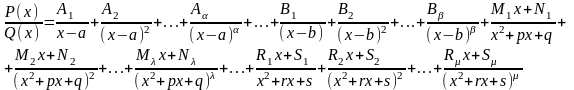
8.Интегрирование функций, содержащих радикалы.
R(x)={P(x)/Q(x)|P,Q-многочлены}
R(f)-класс функций получ. Из класса N, если если вставить в верхнее выражение функцию f.
R(x,f)-класс функций,если вставляя вместо некоторых букв х.
R(f,g)-класс функций,полученный из R, если вместо х вставить f, а в остальные g.
Другими словами из класса R(x), заменой переменной х на какие-то выражения можно получить другие классы функций.
Не от всех классов функций можно взять конечный интеграл.
В основном они сводяться заменой переменной.
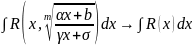
9.Интегрирование биноминальных дифференциалов.
Определение: Биноминальным дифференциалом называется выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
Если р – целое число, то интеграл рационализируется с помощью подстановки
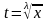 ,
где
- общий знаменатель m
и n.
,
где
- общий знаменатель m
и n.
Если
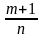 - целое число, то интеграл рационализируется
подстановкой
- целое число, то интеграл рационализируется
подстановкой
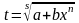 ,
где s
– знаменатель числа р.
,
где s
– знаменатель числа р.
3) Если
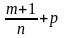 - целое число, то используется подстановка
- целое число, то используется подстановка
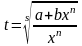 ,
где s
– знаменатель числа р.
,
где s
– знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы
вида
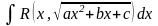 .
.
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
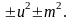
Таким образом, интеграл приводится к одному из трех типов:
10.Подстановки Эйлера. (1707-1783)
Если а>0, то интеграл вида
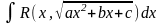 рационализируется подстановкой
рационализируется подстановкой
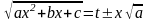 .
.
Если a<0 и c>0, то интеграл вида рационализируется подстановкой
 .
.
Если a<0 , а подкоренное выражение раскладывается на действительные множители a(x – x1)(x – x2), то интеграл вида рационализируется подстановкой
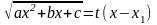 .
.
Отметим, что подстановки Эйлера неудобны для практического использования,
т.к. даже при несложных подинтегральных функциях приводят к весьма громоздким вычислениям. Эти подстановки представляют скорее теоретический интерес.