
- •1.Неопределенный интеграл.
- •2. Первообразные элем.Функций.
- •3.Замена переменных в неопр.Интегралле.
- •4.Интегрирование по частям.
- •5.Интегрирование иррациональных функций.
- •6.Элементарные рац.Функции и интегралы от них.
- •7.Алгоритм
- •8.Интегрирование функций, содержащих радикалы.
- •9.Интегрирование биноминальных дифференциалов.
- •11.Тригонометрическая подстановка.
- •12.Интегр.Функций содержащих показ.Функции
- •13.Определенный интеграл.
- •14.Класс интегрируемых функций
- •15.Определенный интеграл как функция верхнего предела
- •16.Теорема: (Теорема Ньютона – Лейбница)
- •17.Замена переменных.
- •18.Интегрирование по частям.
- •19.Приложения опред. Интеграла
- •1)Площадь плоской фигуры.
- •22.Интеграл Эйлера I рода
- •23.Интеграл Эйлера I I рода
- •24.Функции нескольких переменных
- •25. Непрерывные функции
- •26.Дифференцирование функций нескольких переменных.
- •27.Производная сложной функции
- •28.Частные дифференциалы и дифференциал функции
- •29.Частные производные высших порядков.
- •30.Дифференциалы высших порядков.
- •31.Формула Тейлора
- •32.Градиент.
- •33.Экстремум функции нескольких переменных.
- •34.Теорема. (Достаточные условия экстремума).
- •35.Условный экстремум.
- •36.Билинейная и квадратичная форма
- •38.Второй дифф.Как квадрат.Форма
- •39.Пространства.
- •40.Основные понятия теории дифференциальных уравнений.
- •41.Дифференциальные уравнения первого порядка
- •42.Уравнения с разделяющимися переменными.
- •43.Однородное дифференциальное уравнение первого порядка.
- •44.Уравнения, приводящиеся к однородным. К таким уравнениям относят уравнения вида:
- •45.Линейное уравнение первого порядка
- •46.Уравнение Бернулли
- •47.Уравнение Риккати
- •48.Уравнение в полных дифференциалах и их решение
- •49.Интегральный множитель и его нахождение
- •50.Дифференциального уравнения n-го порядка.
- •51.Диф.Ур.Высшего порядка.Способы пониж.Порядка
- •Уравнения, не содержащие явно искомой функции
- •52.Линейные однородные дифференциальные уравнения с
- •Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
- •54.Метод вариации
- •55.Метод неопределенных коэффициентов.
- •56.Метод Коши
- •57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •58.Нормальные системы обыкновенных дифференциальных уравнений.
- •59.Метод сведения к одному уравнению.
- •60.Метод интегрируемых комбинаций
- •61. Нормальные системы обыкновенных дифференциальных уравнений.
- •62.Фундаментальная система решений как базис линейного пространства решений однородной линейной системы
- •68.Определитель Вронского
- •64.Системы линейных уравнений первого порядка с постоянными коэффициентами: однородные и неоднородные. Структура решения. Алгоритм решения.
- •65.Преобразование Лапласа.
- •66.Интегралл Лапласа и его свойства
- •67.Свойства 1-6 преобразования Лапласа.
- •68.Свойства 7-12 преобразования Лапласа.
- •70.Таблица изображений некоторых функций.
- •72.Интеграл Дюамеля
- •73.Достаточные условия существования оригинала
- •75.Решение уравнений методом Дюамеля.
54.Метод вариации
На практике удобно применять метод вариации произвольных постоянных.
Для этого сначала находят общее решение соответствующего однородного уравнения в виде:
Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:
Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:
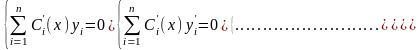
Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.
55.Метод неопределенных коэффициентов.
Суть этого метода состоит в том, что заранее предполагается вид множителей – многочленов, на которые разлагается данный многочлен. Этот метод опирается на следующие утверждения:
1)два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х;
2)любой многочлен третьей степени разлагается в произведение линейного и квадратного множителей;
3)любой многочлен четвертой степени разлагается в произведение двух многочленов второй степени.
Его можно применять тогда, когда по внешнему виду уравнения можно определить общий вид искомой функции. Это относится, прежде всего, к тем случаям, когда решения уравнений следует искать среди целых или дробно рациональных функций.
56.Метод Коши
57.Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Решение
дифференциального уравнения вида
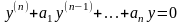 или, короче,
или, короче,
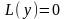 будем искать в виде
будем искать в виде
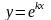 ,
где k
= const.Т.к.
,
где k
= const.Т.к.
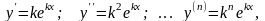 то
то
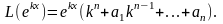 При
этом многочлен
При
этом многочлен
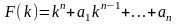 называется характеристическим
многочленом дифференциального
уравнения.
называется характеристическим
многочленом дифференциального
уравнения.
Для того, чтобы функция являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы
 т.е.
т.е.
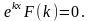
Т.к.
ekx
0, то
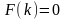 - это уравнение называется характеристическим
уравнением.
- это уравнение называется характеристическим
уравнением.
Как
и любое алгебраическое уравнение
степени n,
характеристическое уравнение
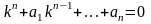 имеет n
корней.
Каждому корню характеристического
уравнения ki
соответствует
решение дифференциального уравнения.
имеет n
корней.
Каждому корню характеристического
уравнения ki
соответствует
решение дифференциального уравнения.
В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.
Правая часть линейного неоднородного дифференциального уравнения имеет вид:
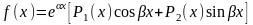
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:
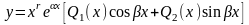
где
число r
показывает сколько раз число
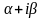 является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x)
и
Q2(x)
– многочлены степени не выше m,
где m-
большая из степеней m1
и m2.
является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x)
и
Q2(x)
– многочлены степени не выше m,
где m-
большая из степеней m1
и m2.
