1.5. Розв’язування матричних рівнянь

Рівняння вигляду AX = B, YC = D називаються простішими матричними рівняннями, де А і С - неособливі квадратні матриці, B і D – задані матриці, X і Y – невідомі матриці.

Якщо матриця A квадратна неособлива матриця, тоді існує обернена до A матриця A^-1 , тому можна рівняння AX = B помножити на A^-1 зліва. Одержимо A^-1AX=A^-1B (11)

За означенням оберненої матриці маємо: A^-1A=E.

Тому (11) прийме вигляд: EX=A^-1B

Але множення матриці-стовпця X на матрицю E не змінює X, тобто EX=X .

Таким чином, одержуємо формулу: X=A^-1B (12)

Аналогічно: YC = D; YC ^-1 = DC ^-1; Y = DC ^-1 (13)

Приклад 9. Розв’язати матричне рівняння

Розв’язання. Позначимо матриці

Отримаємо рівняння AX = B, де X=A^-1B

(обернену матрицю ми знайшли в прикладі 7)

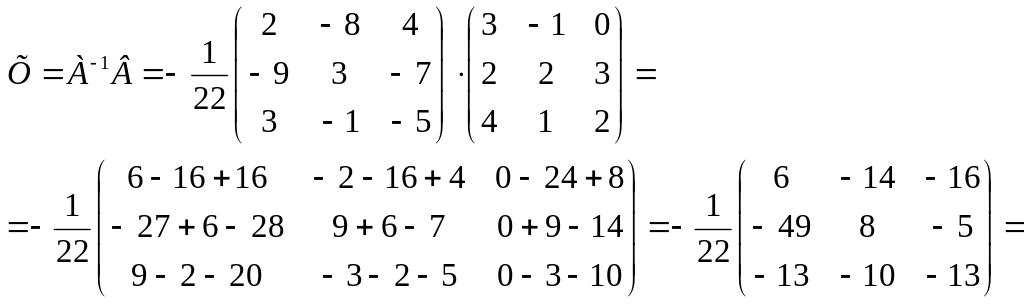
2. Системи лінійних алгебраїчних рівнянь

1. Різновиди систем лінійних алгебраїчних рівнянь

Означення 1. Система алгебраїчних рівнянь називається лінійною, якщо вона може бути записана у вигляді

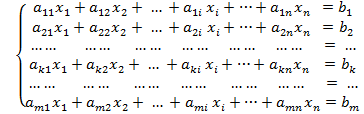(1)

де х₁, х₂, … ,х_n - невідомі; _іj – дійсні числа, які називають коефіцієнтами системи (індекс і вказує рівняння, а індекс j невідоме, при якому записано цей коефіцієнт);

b_k (k =1, 2,…, m) – вільні (від невідомих) члени або їх називають правими частинами рівнянь.

Якщо b_k = 0 для усіх k = 1,2, …, m, тоді систему називають однорідною. Якщо хоч би один вільний член b_k не дорівнює нулю, тоді система алгебраїчних рівнянь називається неоднорідною.

Означення 2. Розв’язком системи (1) називається множина дійсних чисел , , …, , підстановка яких у систему замість невідомих x₁, x₂, …, x_n , перетворює кожне рівняння системи у тотожність (іноді кажуть, що ця множина задовольняє систему рівнянь).

Означення 3. Система лінійних алгебраїчних рівнянь, що має хоч би один розв’язок, називається сумісною, а система, що не має розв’язку, називається несумісною.

2.2. Теорема Кронекера - Капеллі

Німецький математик Леопольд Кронекер ( 1823-1891) та італійський математик Альфред Капеллі (1855-1910) довели дуже важливу теорему, яка використовується у багатьох випадках.

Позначимо через А основну матрицю системи (1), яка складена з коефіцієнтів при невідомих, а через – розширену матрицю цієї системи, яка одержана шляхом доповнення матриці А стовпцем вільних членів, тобто

_{; .}

Теорема Кронекера - Капеллі. Система лінійних алгебраїчних рівнянь (1) сумісна тоді і тільки тоді, коли ранг основної матриці системи дорівнює рангу розширеної матриці r(A) = r( ) (2)

причому, система має єдиний розв’язок тоді і тільки тоді, коли

r(A) = r( ) = n (3)

Приклад 1. Дослідити сумісність системи

Розв’язання. Задана неоднорідна система трьох лінійних алгебраїчних рівнянь з чотирма невідомими. Для перевірки умови (2) теореми Кронекера-Капеллі знайдемо ранги основної та розширеної матриць заданої системи, застосовуючи до матриць елементарні перетворення.

Розширену матрицю одержуємо шляхом дописування до основної матриці системи стовпця вільних членів.

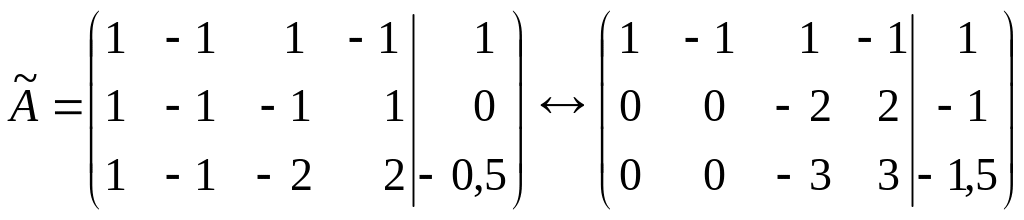
Еквівалентну матрицю отримали шляхом множення елементів першого рядка на (-1) та додавання до елементів другого та третього рядків. Тепер елементи другого рядка помножимо на і додамо до елементів третього рядка, а потім поміняємо місцями другий та третій стовпчики.

З останнього запису випливає, що r( ) = 2 та r(A) = 2 , тобто r(A) = r( ), а це означає, що задана система рівнянь є сумісною.