Матричный метод решения систем линейных уравнений.

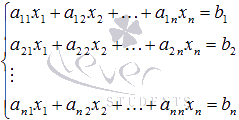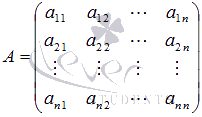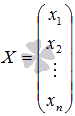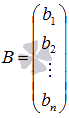В этой статье поговорим о матричном методе решения систем линейных алгебраических уравнений вида , которые в матричной форме записываются как , где - основная матрица системы, - матрица-столбец неизвестных переменных, - матрица свободных членов. Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров. Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения. Приступим. Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравнения слева на (порядки матриц A ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как , а по определению обратной матрицы (E – единичная матрица порядка n на n), поэтому 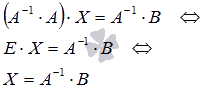Таким образом, решение системы линейных алгебраических уравнений по матричному методу определяется равенством . Другими словами, решение СЛАУ находится с помощью обратной матрицы . Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ. Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы. Пример. С помощью обратной матрицы найдите решение системы линейных уравнений . Решение. В матричной форме исходная система запишется как , где 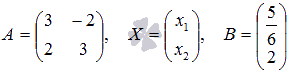. Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем 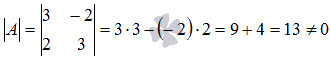, следовательно, для матрицы А может быть найдена обратная матрица . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как . Итак, задача свелась к построению обратной матрицы . Найдем ее. Мы знаем, что для матрицы обратная матрица может быть найдена как 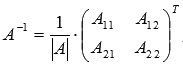, где - алгебраические дополнения элементов . В нашем случае Тогда Выполним проверку полученного решения , подставив его в матричную форму исходной системы уравнений . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка. Следовательно, решение найдено верно. Ответ: или в другой записи .

Системы линейных уравнений: основные понятия

24 Июня 2011

Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Определение. Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.

2. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.

3. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Определение. Переменная x_i называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

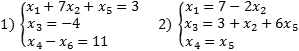
Обе системы являются разрешенными относительно переменных x₁, x₃ и x₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x₁, x₃ и x₅. Достаточно переписать самое последнее уравнение в виде x₅ = x₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

1. Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x₁ = b₁, x₂ = b₂, ..., x_k = b_k;

2. Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x₂, x₅, x₆ (для первой системы) и x₂, x₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Теорема. Если в системе из n уравнений переменные x₁, x₂, ..., x_r — разрешенные, а x_{r + 1}, x_{r + 2}, ..., x_k — свободные, то:

1. Если задать значения свободным переменным (x_{r + 1} = t_{r + 1}, x_{r + 2} = t_{r + 2}, ..., x_k = t_k), а затем найти значения x₁, x₂, ..., x_r, получим одно из решений.

2. Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.