Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.

.

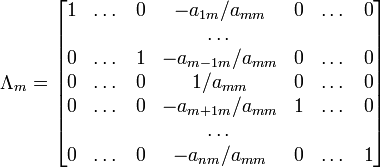Вторая матрица после применения всех операций станет равна , то есть будет искомой. Сложность алгоритма — .

С помощью матрицы алгебраических дополнений

— транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

Использование lu/lup-разложения

Матричное уравнение для обратной матрицы можно рассматривать как совокупность систем вида . Обозначим -ый столбец матрицы через ; тогда , ,поскольку -м столбцом матрицы является единичный вектор . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение . Пусть , . Тогда из свойств обратной матрицы можно записать: . Если умножить это равенство на U и L то можно получить два равенства вида и . Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство .

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору , обеспечивающие выполнение условия (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы (а именно, если A — симметричная положительно определённая матрица и , то можно взять , где ; если же A — произвольная невырожденная матрица и , то полагают , где также ; можно конечно упростить ситуацию и, воспользовавшись тем, что , положить ). Во-вторых, при таком задании начальной матрицы нет гарантии, что будет малой (возможно, даже окажется ), и высокий порядок скорости сходимости обнаружится далеко не сразу.