Сравнение бесконечно малых. Эквивалентно бесконечно малые.
Сравнение бесконечно малых.
Пусть α(x) и β(x) две бесконечно малые функции при x → x0 и β(x) отлична от нуля в некоторой окрестности точки х0 (за исключением, быть может, самой точки х0). Если
= 0,то α(x) называется
бесконечно малой более высокого порядка,
чем β(x). В этом случае пишут α(x) = o(β(x)) и
говорят α(x) есть о − малое от β(x).
Если = А ≠ 0 ( A - число),то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = O(β(x)), (α(x) есть O - большое от β(x).
Если = ∞,то α(x) называется бесконечно малой более низкого порядка, чем β(x).
Если = 1,то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x).
В
некоторых случаях недостаточно знать,
что одна из двух бесконечно малых
является бесконечно малой более высокого
порядка, чем другая. Нужно еще оценить,
как высок этот порядок. Поэтому вводится
следующее правило: если
,то
α(x) является бесконечно малой n -го
порядка относительно β(x).
Теорема. Для того, чтобы две функции f = f (x) и g = g (x), f (x) ≠ 0, g (x) ≠ 0, были эквивалентными при х → х0, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий
f - g = o(f ) или f - g = o(g).
Доказательство
необходимости.
Пусть
,
тогда
,
откуда
,
то есть g − f = o(g). Аналогично из условия
доказывается g − f = o(f )
Эквиваленты.
1.Так
как
, то в точке х = 0 имеем sin x ~ x, и в этом
случае имеет место равенство sin x = x +
o(x).
2.Так
как
, то в точке х = 0 имеем tg x ~ x, и в этом
случае имеет место равенство tg x = x +
o(x).
3.Так
как
, то в точке х = 0 имеем arcsin x ~ x, и в этом
случае имеет место равенство arcsin x = x +
o(x).
4.Так
как
,
то в точке х = 0 имеем arctg x ~ x, и в этом
случае имеет место равенство arctg x = x +
o(x).
5.Так
как
,
то
,
и в этом случае имеет место равенство
6.В
точке х = 0 многочлен эквивалентен своему
моному младшей степени
.
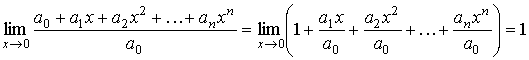Поэтому при х = 0 имеем
.
7.Так
как
,
то ln (1 + x) ~ x,
и в этом случае имеет место равенство ln (1 + x) = x + o(x).
8.Так
как
,
то
9.
Так как
,
то
ex ~ 1 + x, и в этом случае имеет место равенство ex ~ 1 + x + o(x).
10.В
случае натурального k имеем
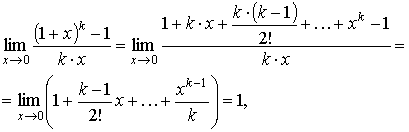поэтому для натурального k имеем , и в
этом случае имеет место равенство
(1 + x)k = 1 + k·x + o(x)
11.
Так как
,
то ax ~ 1 + x·ln a, и в этом случае имеет место
равенство ax ~ 1 + x·ln a + o(x)
12.
Так как
,
то
,
и в этом случае имеет место равенство
Замечание.
К применению таблицы эквивалентности
при вычислении пределов следует
относиться с большим вниманием. Не
следует думать, что этот метод является
всеобъемлющим. Если применение таблицы
эквивалентных бесконечно малых приводит
к конечному результату при вычислении
предела, то этот результат будет
получаться и при любых методах вычисления
этого предела. Следует познакомиться
с образцами выполнения самостоятельной
работы. Однако, в некоторых случаях этот
метод не выводит предел из неопределённости,
вопрос о значении предела остаётся
открытым и посему следует уже применять
другие методы вычисления предела.
Например
Теорема о предельном переходе под знаком неравенства. Теорема о сжатой переменной (формулировка).
Теорема о предельном переходе под знаком неравенства-?
Теорема о сжатой переменной (формулировка)
Формулировка: Если существуют 3 последовательности, элементы одной из которых начиная с некоторого номера будут между элементами двух других при равных номерах, а также 2 другие последовательности имеют конечные пределы, и эти пределы равны, то наша последовательность тоже будет сходится к конечному пределу,и этот предел будет равен пределам двух других последовательностей.