92. Рассмотрев последовательность частичных сумм ряда, докажите, что при ряд расходится.

Это геометрическая прогрессия, где b₁=1,b₂=q,b=q²

Sn=b1*(qⁿ-1)/(q-1)= (qⁿ-1)/(q-1)

При |q|>=1и n→∞ (по условию), значит, qⁿ→∞. Значит Sn=qⁿ-1/(q-1)=∞. Значит ряд расходится.

93. Может ли ряд cходиться, если ряд сходится, а ряд

расходится?

Ряд ∑_(n=1)(a_n+b_n) будет сходиться, если будут сходиться два ряда ∑_(n=1)a_n и ∑_(n=1)b_n.

Но так как это условие не выполняется (b_n-расходится), то сумма двух числовых рядов a_n и b_n тоже будет расходиться.

94. Необходимый признак сходимости. Если ряд сходится, то предел его общего члена равен нулю. Эквивалентная формулировка: Если предел общего члена ряда не равен нулю или не существует, то данный ряд расходится.

Доказательство. Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем 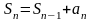, или 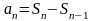(*). При 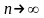обе частичные суммы 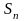и 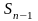стремятся к пределу S, поэтому из равенства (*) следует, что 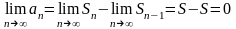. Мы установили только необходимое условие сходимости ряда, т. е. условие, при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать только расходимость ряда.

Пример: 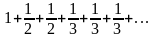В этом случае предел общего члена ряда, очевидно, равен нулю, однако ряд расходится. Действительно, если бы данный ряд сходился, то сходился бы и ряд 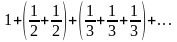, полученный из данного ряда группировкой членов. Но общий член последнего ряда равен 1, и для него не выполнен необходимый признак сходимости.

96. Докажите, что для сходимости ряда n, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Теорема. Для того чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Доказательство. Необходимость. Пусть ряд 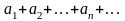сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует, что последовательность частичных сумм ограничена. Достаточность. Поскольку все члены данного ряда положительны и для любого n , то последовательность его частичных сумм монотонно возрастает. Однако известно, что ограниченная сверху монотонная последовательность имеет предел.

97 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.

Признак Даламбера: Пусть дан ряд ∑а_n при n= (1; ∞) c положительными членами и сущ. lim= a_{n+1 ÷} a_n =d. Тогда А) при d< 1 ряд сходится; б) d > 1 ряд расходится.

Док - во: а). Пусть lim Аn+1÷An = d (при n стремится к ∞). Для любого E>0 сущ N≥n и │An+1÷An - d│< E/

-E< An+1÷An< E+d

d-E<An+1÷An<E+d. Возьмем Е таким, чтобы d+E<1, тогда d+E=q , следовательно, An+1÷An<q → An+1<q*An

A2<A1*q

A3<A2*q = A1*q²

A1<A3*q = A1*q³

(1) (2)

эта система бесконечно убыв прогрессия

An+1<An*q<A1*qⁿ

Члены ряда (1) меньше членов ряда (2), а (2) сходится и в силу 1ого признака сравнения (1) ряд тоже сходится.

Б) lim An+1÷ An=d

│An+1÷An -d│< E

-E<An+1÷An -d<E

d-E<An+1÷An<E+d

Пусть Е будет таким, что d-E>1, d-E=q → An+1÷An> q → An+1>An*q → An+1> An→ Общий член послед не стремится к нулю, следовательно, ряд расходится.