6. Прямая, перпендикулярная плоскости.

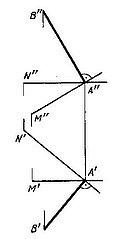П рямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым этой плоскости. Признак перпендикулярности прямой и плоскости можно сформулировать в виде теоремы.

ТЕОРЕМА: Для того, чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна горизонтали, а фронтальная проекция прямой – фронтали.

Для задания прямой перпендикулярной плоскости в качестве пересекающихся прямых удобно выбрать линии уровня – фронталь и горизонталь. В этом случае можно воспользоваться свойствами проекций прямого угла.

7. Горизонталь и фронталь в плоскостях общего положения и проецирующих.

Плоскость, не перпендикулярная ни одной плоскости проекции, называется плоскостью общего положения.

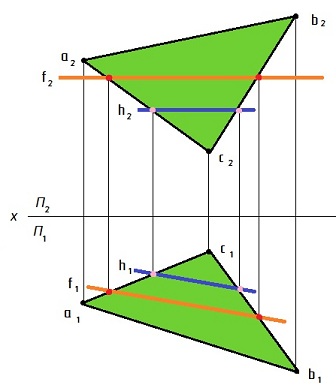
Такая плоскость пересекает все плоскости проекций и имеет три следа: горизонтальный, фронтальный и профильный.

Плоскости, перпендикулярные плоскостям проекции, занимают частное положение в пространстве и называются проецирующими.

8. Определение истиной величины отрезка прямой методом вращения.

С пособ вращения заключается в том, что геометрический объект вращается в пространстве вокруг выбранной оси до требуемого положения относительно плоскостей проекций. Точки вращаемого предмета описывают в пространстве дуги окружностей, лежащих в плоскостях, перпендикулярных к оси вращения, а центры этих окружностей располагаются на оси вращения в точках пересечения оси с плоскостями. В качестве осей вращения можно брать либо проецирующие прямые, либо прямые уровня.

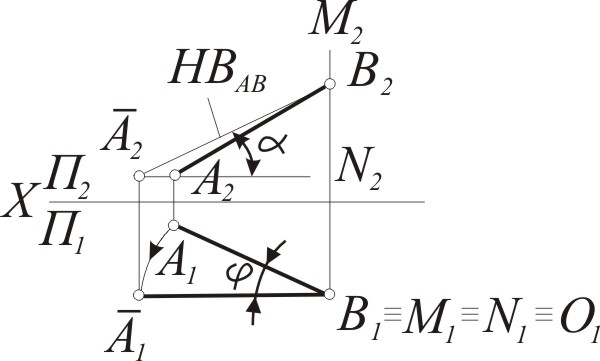
Для определения натуральной (истиной) величины отрезка прямой достаточно ось вращения с проекциями M₂N₂, M₁N₁ выбрать так, чтобы она проходила через одну из крайних точек отрезка, например, точку с проекциями В₁В₂. Тогда при повороте точки А на угол в положение , отрезок АВ перемещается в положение АВ П₁ и, следовательно, проецируется на неё в натуральную величину. Одновременно в натуральную величину будет проецироваться угол наклона отрезка АВ к плоскости П₂.

9. Метод конкурирующих точек.

Т очки, у которых проекции на П₁ совпадают, называют конкурирующими по отношению к плоскости П₁, а точки, у которых проекции на П₂ совпадают, называют конкурирующими по отношению к плоскости П₂.

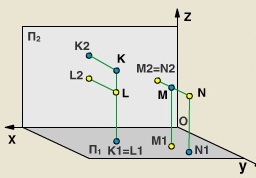
Т 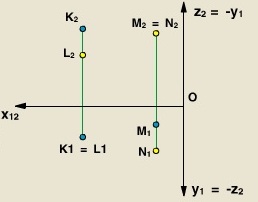очки К и L конкурирующие по отношению к плоскости П₁, так как на плоскости П₁ точки К и L проецируются в одну точку: К₁ = L₁. Точка К выше точки L, т.к. К₂ выше точки L₂, потому К₁ на П₁ видима.

Точки N и М конкурирующие по отношению к плоскости П₂, так как на плоскости П₂ точки M и N проецируются в одну точку: М₂ = N₂. Точка N ближе к наблюдателю, чем точка М, т.к. координата у точки N больше, чем у точки М, а потому точка N закрывает точку М, а потому N₁ на П₂ является видимой.

10. Плоскости общего положения, уровня и проецирующие. Точки и прямые в указанных плоскостях.

П 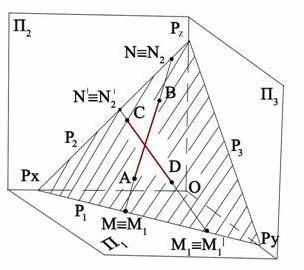лоскость общего положения – плоскость, произвольно расположенная по отношению к плоскостям проекций (рис.).

Проекции элементов, которыми задана такая плоскость (точки, прямые, следы плоскости, плоские фигуры), составляют случайные углы с линиями связи и осями проекций комплексного чертежа, т.е. располагаются произвольно и ни в одной проекции не выражаются простым геометрическим образом.

Плоскости, перпендикулярные одной или двум плоскостям проекций называются плоскостями частного положения.

Плоскость, перпендикулярная к плоскости проекций называется проецирующей плоскостью. Проецирующая плоскость, перпендикулярная к горизонтальной плоскости проекций называется горизонтально-проецирующей, к фронтальной – фронтально-проецирующей, к профильной – профильно-проецирующей.

В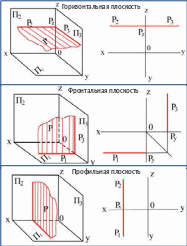 прямоугольных проекциях плоскость, перпендикулярная к плоскости проекций, параллельна направлению проецирования и поэтому является проецирующей. Её проекция на этой плоскости выражается прямой; проекция на другую плоскость является неограниченным полем точек.

Плоскость, параллельная плоскости проекций называется плоскостью уровня. Такая плоскость перпендикулярна к двум другим плоскостям проекций и является проецирующей, проецируется в прямую линию. Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной, параллельная фронтальной – фронтальной и параллельная профильной – профильной плоскостью уровня.

Плоскости уровня не имеют следа на параллельной себе плоскости проекций и проецируются на неё в неограниченные поля точек (эти проекции на комплексном чертеже не обозначаются и не ограничиваются).

Положение плоскостей уровня подчинено общему правилу: если плоскость параллельна плоскости проекций, то на эту плоскость она проецируется в поле точек. Её проекция на другой плоскости – прямая, перпендикулярная к линии связи.