
- •Электрическая цепь. Эл ток, напряжение, эдс. Идеализированные и реальные элементы цепей. Управляемые источники тока и напряжения.
- •1.2Пассивные дифференцирующие цепи
- •2.2Пассивные интегрирующие цепи
- •3 .1.Переменный син-ый ток. Определение основных понятий. Действующее и среднее значение переменного тока.
- •3.2Метод контурных токов (Максвела)
- •4.1.Изображение синусоидальных величин с помощью вращающихся векторов и комплексных чисел.
- •4.2Метод узловых потенциалов (напряжений)
- •5.2.Метод эквивалентного генератора(эг)
- •7 .1.Ток и напряжение в цепи при параллельном соединении rlc.
- •7 .2.Резонанс напряжений. (Схема и векторная диаграмма)
- •11.1. Три формулы мощности.
- •12.1.Индуктивносвязанные цепи.
- •12.2. Единичная импульсная функция
- •13.1. Уравнение равновесия напряжений в индуктивно-связанной системе. Векторная диаграмма. Трансформаторы.
- •13.2.Полевые транзисторы как нелинейные управляемые сопротивления. Вах. Параметры. Применение.
- •1. Ряд Фурье. Спектры периодических сигналов. Расчет электрических цепей при несинусоидальных периодических эдс, напряжениях и токах.
- •14.2) Нелинейные резистивные цепи постоянного тока. Графические методы расчета. Метод пересечений. Метод эквивалентного генератора. Итерационный метод.
- •15.2.Расчёт переходных процессов с помощью интеграла Дюамеля
- •16.1.Классический метод расчёта переходных процессов
- •17. 1)Включение цепи r, l, с на постоянное напряжение (случай; апериодический и предельный апериодический).
- •17.2) Расчет разветвленных магнитных цепей на постоянном токе
- •18) Включение цепи r, l, с на постоянное напряжение (колебательный случай).
- •18.2) Нелинейное сопротивление при гармоническом воздействии. Понятие о режиме малого и большого сигнала.
- •19.1)Расчёт переходных процессов операторным методом
- •19.2)Нелинейные цепи переменного тока. Методы расчета. Диодные ограничители амплитуды. Расчет. Применение.
- •20. 1) Порядок расчёта переходных процессов операторным методом. Переход от изображений к оригиналам
- •20.2) Контуры с неполным включением индуктивности и емкости. Ачх и фчх.
3 .1.Переменный син-ый ток. Определение основных понятий. Действующее и среднее значение переменного тока.
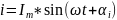
Мгновенное значение i - его значение для любого t.
Амплитуда i - наибольшее значение из мгновенных значений.
Фаза (текущая фаза) – аргумент sin (угол стоящий под знаком sin)/
Начальная
фаза – значение угла при t=0
(
0< опережение по фазе.
опережение по фазе.
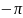 <
<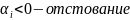 по
фазе.
по
фазе.
Р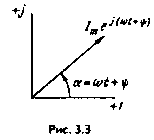 азность
фаз (угол сдвига фаз двух sin)
– разность значения их фаз.
азность
фаз (угол сдвига фаз двух sin)
– разность значения их фаз.
Период sin (T) – промежуток, в котором функция претерпевает полный цикл изменений, а потом повторяется.
Частота – число периодов за 1 сек.
f=1/T
[Гц],

f=50 Гц - промышленная частота.
Длина волны – длина, на которой происходит изменение направления электронов за период.

Короткие линии-такие линии тока, напряжение на которых являет. только функцией времени.
Действующее значение переменного тока – называется такой воображаемый постоянный ток, который в течении периода выделяет такое же кол-во тепла что и переменный ток.
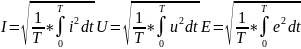 .
.
I,U,E-совпадают с определением среднеквадратического значения тока, напряжения, эдс.
Когда говорят о токе, имеют в виду действующее значение.
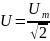
Среднее значение переменного тока – это такой воображаемый постоянный ток, который в течении полупериода проносит через эл цепь такое же кол-во электричества что и переменный ток.

3.2Метод контурных токов (Максвела)
Целесообразно применять когда много узлов и мало векторов.
Контурный ток – ток, имеющий в данном контуре одно и тоже значение как по величине, так и по направлению.
В общем случае, контурный ток не является реальным током. Он будет реальным, если протекает по внешней ветви.

![]() (1)
(1)
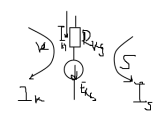
 (2)
(2)
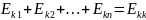
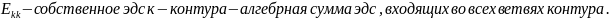
(1)В
(2)
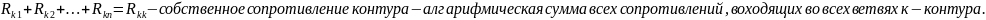
 (имеет
знак!).
(имеет
знак!).
Если направления контурных токов совпадают то «+», не совпадают «-».
 (3)
(3)
 (4)
(4)
Решая (4) находим контурные токи, затем из (1) находим реальные токи. Проверяем баланс мощностей.
4.1.Изображение синусоидальных величин с помощью вращающихся векторов и комплексных чисел.
Из
курса математики известна формула
Эйлера:

На
комплексной плоскости число
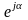 изображают
численно равным единице и составляющим
угол
изображают
численно равным единице и составляющим
угол
 с осью вещественных значений (осью +1).
Угол
отсчитываем против часовой стрелки от
оси +1. Модуль функции:
с осью вещественных значений (осью +1).
Угол
отсчитываем против часовой стрелки от
оси +1. Модуль функции:
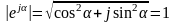
Проекция
функции
на
ось +1 равна
 ,
а на ось +j
равна
,
а на ось +j
равна
 .
.
Заменим
на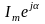 .
.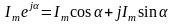 .
.
Возьмём
угол зависящий от времени:
 ,
тогда:
,
тогда:
 ;
;
 -представляет собой действительную
часть Re
выражения
-представляет собой действительную
часть Re
выражения
 =>
=>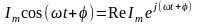 ;
;
 -представляет собой коэффициент при
мнимой части Im
выражения
=>
-представляет собой коэффициент при
мнимой части Im
выражения
=>
Значит
мгновенный ток i
можно представить как
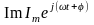 или
как проекцию вращающегося вектора
на
ось +j.
или
как проекцию вращающегося вектора
на
ось +j.
Обычно
вектора изображают для момента времени
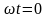 ,
тогда
,
тогда
 ,
где
,
где
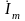 -
комплексная величина,
-
комплексная величина,
 -
угол, под которым вектор
проведён
к оси +1 на комплексной плоскости, равный
начальной фазе.
называется
комплексной
амплитудой
тока
-
угол, под которым вектор
проведён
к оси +1 на комплексной плоскости, равный
начальной фазе.
называется
комплексной
амплитудой
тока
 ,
она изображает ток для момента времени
.
Точка над током или напржением означает,
что он изменяется по синусоидальному
закону.Переход от комплексной амплитуды
к мгн. знач. умножим
на
,
она изображает ток для момента времени
.
Точка над током или напржением означает,
что он изменяется по синусоидальному
закону.Переход от комплексной амплитуды
к мгн. знач. умножим
на
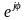 .
. Для
радиотехники наибольшее значение имеет
действующее знач. тока.
Для
радиотехники наибольшее значение имеет
действующее знач. тока. .
.
Сложение синусоидальных функций времени.
П![]() оложим,
что необходимо сложить два тока (
оложим,
что необходимо сложить два тока (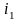 и
и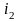 ),
одинаковой частоты. Сумма их дает
некоторый ток той же частоты:
),
одинаковой частоты. Сумма их дает
некоторый ток той же частоты:
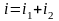 ;
;
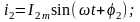
 Требуется
найти амплитуду
Требуется
найти амплитуду
 и начальную фазу
тока i
. Изобразим на комплексной плоскости
(рис. 3.4) токи и их геометрическая сумма
и будет искомым вектором, у которого
амплитуда тока
определяется длинной суммарного
вектора, а начальная фаза
- углом м/д этим вектором и осью +1.
и начальную фазу
тока i
. Изобразим на комплексной плоскости
(рис. 3.4) токи и их геометрическая сумма
и будет искомым вектором, у которого
амплитуда тока
определяется длинной суммарного
вектора, а начальная фаза
- углом м/д этим вектором и осью +1.
Для
вычитания двух токов
(ЭДС, U)
следует на комплексной плоскости
произвести не сложение, а вычитание
соответствующих векторов.При изменении
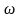 взаимное расположение остаётся
постоянным (вектора вращаются относительно
начала координат).Векторной
диаграммой
называют совокупность векторов на
комплексной плоскости, изображающих
синусоидально изменяющиеся функции
времени одной к той же частоты и
построенных с соблюдением правильной
ориентации их относительно друг друга
по фазе. Пример изображён на рис
3.4.Перемножение
синусоидальных функций времени
происхо-дит
по формулам преобразования
тригонометрических функций:
взаимное расположение остаётся
постоянным (вектора вращаются относительно
начала координат).Векторной
диаграммой
называют совокупность векторов на
комплексной плоскости, изображающих
синусоидально изменяющиеся функции
времени одной к той же частоты и
построенных с соблюдением правильной
ориентации их относительно друг друга
по фазе. Пример изображён на рис
3.4.Перемножение
синусоидальных функций времени
происхо-дит
по формулам преобразования
тригонометрических функций:

