
- •Электрическая цепь. Эл ток, напряжение, эдс. Идеализированные и реальные элементы цепей. Управляемые источники тока и напряжения.
- •1.2Пассивные дифференцирующие цепи
- •2.2Пассивные интегрирующие цепи
- •3 .1.Переменный син-ый ток. Определение основных понятий. Действующее и среднее значение переменного тока.
- •3.2Метод контурных токов (Максвела)
- •4.1.Изображение синусоидальных величин с помощью вращающихся векторов и комплексных чисел.
- •4.2Метод узловых потенциалов (напряжений)
- •5.2.Метод эквивалентного генератора(эг)
- •7 .1.Ток и напряжение в цепи при параллельном соединении rlc.
- •7 .2.Резонанс напряжений. (Схема и векторная диаграмма)
- •11.1. Три формулы мощности.
- •12.1.Индуктивносвязанные цепи.
- •12.2. Единичная импульсная функция
- •13.1. Уравнение равновесия напряжений в индуктивно-связанной системе. Векторная диаграмма. Трансформаторы.
- •13.2.Полевые транзисторы как нелинейные управляемые сопротивления. Вах. Параметры. Применение.
- •1. Ряд Фурье. Спектры периодических сигналов. Расчет электрических цепей при несинусоидальных периодических эдс, напряжениях и токах.
- •14.2) Нелинейные резистивные цепи постоянного тока. Графические методы расчета. Метод пересечений. Метод эквивалентного генератора. Итерационный метод.
- •15.2.Расчёт переходных процессов с помощью интеграла Дюамеля
- •16.1.Классический метод расчёта переходных процессов
- •17. 1)Включение цепи r, l, с на постоянное напряжение (случай; апериодический и предельный апериодический).
- •17.2) Расчет разветвленных магнитных цепей на постоянном токе
- •18) Включение цепи r, l, с на постоянное напряжение (колебательный случай).
- •18.2) Нелинейное сопротивление при гармоническом воздействии. Понятие о режиме малого и большого сигнала.
- •19.1)Расчёт переходных процессов операторным методом
- •19.2)Нелинейные цепи переменного тока. Методы расчета. Диодные ограничители амплитуды. Расчет. Применение.
- •20. 1) Порядок расчёта переходных процессов операторным методом. Переход от изображений к оригиналам
- •20.2) Контуры с неполным включением индуктивности и емкости. Ачх и фчх.
17. 1)Включение цепи r, l, с на постоянное напряжение (случай; апериодический и предельный апериодический).
З аданы
параметры цепи: R,
L,
C;
напряжение U
;
независимые начальные условия:
аданы
параметры цепи: R,
L,
C;
напряжение U
;
независимые начальные условия:
 ,
,
 (1.41)
(1.41)
Требуется найти ток i и
напряжения
 ,
,
.
Составим интегродифференциальное
уравнение равновесия напряжений в
контуре
,
,
.
Составим интегродифференциальное
уравнение равновесия напряжений в
контуре

Д ля
получения дифференциального уравнения
выразим ток i
через напряжение
:
ля
получения дифференциального уравнения
выразим ток i
через напряжение
:
 ;
;
 (1.43)
(1.43)
Общее
решение уравнения (1.43) имеет вид
 ;
;
 .
.
Свободная
составляющая
 является общим решением однородного
уравнения
является общим решением однородного
уравнения

Соответствующее характеристическое уравнение
 или
или
 . (1.45)
. (1.45)
Характеристическое уравнение (1.45) проще составить, записав для цепи комплексное входное сопротивление
 .
.
При --
--

Приравняв
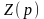 к 0, получим характеристическое уравнение
(1.45).
к 0, получим характеристическое уравнение
(1.45).
Корни уравнения (1.45)
 , (1.46)
, (1.46)
где
 – коэффициент затухания,
– коэффициент затухания, – резонансная частота.
– резонансная частота.
Решение
однородного уравнения (1.44) зависит от
вида корней
 и
и
 .
Из (1.46) следует, что корни могут быть
вещественными неравными (
.
Из (1.46) следует, что корни могут быть
вещественными неравными ( ),
вещественными равными (
),
вещественными равными ( )
и комплексно-сопряжёнными (
)
и комплексно-сопряжёнными (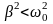 ).
Соответственно различают три случая
свободного процесса в цепи (рис. 1.21):
).
Соответственно различают три случая
свободного процесса в цепи (рис. 1.21):
1.
Апериодический случай – корни
и
– вещественные, отрицательные и
неравные ;
;
 или
.
или
.
Каждый
из корней даёт независимое решение, и
свободная составляющая напряжения на
ёмкости
 ,где
A
и B
– постоянные интегрирования.
,где
A
и B
– постоянные интегрирования.
Переходное
напряжение
примет вид
 ,
,
а
переходный ток в контуре .
(1.49)
.
(1.49)
Найдём
постоянные интегрирования
 и
,
используя начальные условия (1.41) и
законы коммутации,
и
,
используя начальные условия (1.41) и
законы коммутации, ;
;
 .
(1.50)
.
(1.50)
Для
момента
 из (1.48) и (1.49) следует
из (1.48) и (1.49) следует ;
;


откуда ;
;
 .
(1.52)
.
(1.52)
Подставив и в (1.48) и (1.49), получим
 ;
(1.53)
;
(1.53)
 ;
;
Так
как в (1.46)
 ,
то
,
то
Переходные напряжения и найдём по формулам:
 ;
;
 .
.
Графики переходного процесса для , и построены на рис. 1.22, а, б.

Найдём
максимум (амплитуду) импульса переходного
тока (рис. 1.22, б) .
.
Приравняв эту производную нулю, получим время этого максимума
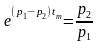


 .
.
Подставив
 в формулу (1.54), найдём
.
в формулу (1.54), найдём
.
3.
Предельный апериодический (критический)
случай: корни
и
(1.46) – вещественные, отрицательные и
равные,
 ,
,
 .
.
В этом граничном случае выражение для просто получить из формулы (1.57):
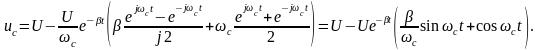 используя
предельный переход при
используя
предельный переход при
 и раскрывая неопределённость
и раскрывая неопределённость
 по правилу Лопиталя:
по правилу Лопиталя:

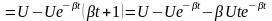 .
(1.66)
.
(1.66)
 .
(1.67)
.
(1.67)
Графики переходного процесса для этого случая показаны на рис. 1.25, а, б.
|
|
Из
формулы (1.66) и графика (рис. 1.25, а) видно,
что напряжение
устанавливается дольше, чем при
апериодическом заряде ёмкости при
равных в обоих случаях постоянных
времени
 и
и
 .
При расчёте по формуле (1.66) напряжение
отличается от
.
При расчёте по формуле (1.66) напряжение
отличается от
 при
при
 на
на
 ,
при
,
при
 на
на
 ,
при
,
при
 на
на
 .
Таким образом, время переходного
процесса
.
Таким образом, время переходного
процесса
 можно считать близким к
.
можно считать близким к
.
В практических случаях представляет интерес амплитуда импульса тока, которым заряжается конденсатор.
Приравняв
производную
 нулю, найдём
нулю, найдём
 и
и
 .
.
Из
равенства
,
при котором корни характеристического
уравнения становятся равными, находят
граничное значение сопротивления
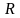 ,
которое называют критическим,
,
которое называют критическим, .
(1.66)
.
(1.66)
При
 переходный процесс имеет апериодический
характер, при
переходный процесс имеет апериодический
характер, при
 процесс становится колебательным.
Добротность контура в критическом
режиме
процесс становится колебательным.
Добротность контура в критическом
режиме
 Контур
с добротностью
Контур
с добротностью
 называют колебательным.
называют колебательным.


