
- •Электрическая цепь. Эл ток, напряжение, эдс. Идеализированные и реальные элементы цепей. Управляемые источники тока и напряжения.
- •1.2Пассивные дифференцирующие цепи
- •2.2Пассивные интегрирующие цепи
- •3 .1.Переменный син-ый ток. Определение основных понятий. Действующее и среднее значение переменного тока.
- •3.2Метод контурных токов (Максвела)
- •4.1.Изображение синусоидальных величин с помощью вращающихся векторов и комплексных чисел.
- •4.2Метод узловых потенциалов (напряжений)
- •5.2.Метод эквивалентного генератора(эг)
- •7 .1.Ток и напряжение в цепи при параллельном соединении rlc.
- •7 .2.Резонанс напряжений. (Схема и векторная диаграмма)
- •11.1. Три формулы мощности.
- •12.1.Индуктивносвязанные цепи.
- •12.2. Единичная импульсная функция
- •13.1. Уравнение равновесия напряжений в индуктивно-связанной системе. Векторная диаграмма. Трансформаторы.
- •13.2.Полевые транзисторы как нелинейные управляемые сопротивления. Вах. Параметры. Применение.
- •1. Ряд Фурье. Спектры периодических сигналов. Расчет электрических цепей при несинусоидальных периодических эдс, напряжениях и токах.
- •14.2) Нелинейные резистивные цепи постоянного тока. Графические методы расчета. Метод пересечений. Метод эквивалентного генератора. Итерационный метод.
- •15.2.Расчёт переходных процессов с помощью интеграла Дюамеля
- •16.1.Классический метод расчёта переходных процессов
- •17. 1)Включение цепи r, l, с на постоянное напряжение (случай; апериодический и предельный апериодический).
- •17.2) Расчет разветвленных магнитных цепей на постоянном токе
- •18) Включение цепи r, l, с на постоянное напряжение (колебательный случай).
- •18.2) Нелинейное сопротивление при гармоническом воздействии. Понятие о режиме малого и большого сигнала.
- •19.1)Расчёт переходных процессов операторным методом
- •19.2)Нелинейные цепи переменного тока. Методы расчета. Диодные ограничители амплитуды. Расчет. Применение.
- •20. 1) Порядок расчёта переходных процессов операторным методом. Переход от изображений к оригиналам
- •20.2) Контуры с неполным включением индуктивности и емкости. Ачх и фчх.
16.1.Классический метод расчёта переходных процессов
Определение переходного процесса
Переходным процессом называется изменение во времени токов и напряжений в электрической цепи при переходе от одного установившегося режима к другому.
Установившийся (стационарный) режим создаётся в цепи источником постоянной ЭДС, источником периодически изменяющейся ЭДС произвольной формы (в том числе синусоидальной). К этому режиму относится также случай отсутствия токов в ветвях цепи.
В отличие от установившегося, переходной режим – неустановившийся, нестационарный процесс, характеризующийся быстрыми изменениями токов и напряжений.
Переходной процесс начинается с мгновенного изменения состояния цепи, называемого к о м м у т а ц и е й: замыкания, размыкания, переключения выключателей, контактов реле и других коммутационных устройств, объединённых общим названием – «ключи» (рис. 1.1). Под это понятие попадают также электронные схемы, работающие в ключевом режиме.
В дальнейшем будем считать, что коммутация
происходит при
дальнейшем будем считать, что коммутация
происходит при
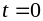 .
Момент времени, предшествующий
коммутации, будем обозначать
.
Момент времени, предшествующий
коммутации, будем обозначать
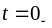 ,
а момент времени сразу после коммутации
–
,
а момент времени сразу после коммутации
–
 .
В момент коммутации в электрической
цепи скачком изменяется приложенное
к ней напряжение или её параметры,
причём переходный процесс возможен
только в такой цепи, в состав которой
входят реактивные элементы – индуктивность
и (или) ёмкость, способные запасать
энергию магнитного и электрического
полей. Переходной процесс отсутствует
в цепях, содержащих лишь активные
сопротивления. При коммутации в таких
цепях токи и напряжения устанавливаются
мгновенно.
.
В момент коммутации в электрической
цепи скачком изменяется приложенное
к ней напряжение или её параметры,
причём переходный процесс возможен
только в такой цепи, в состав которой
входят реактивные элементы – индуктивность
и (или) ёмкость, способные запасать
энергию магнитного и электрического
полей. Переходной процесс отсутствует
в цепях, содержащих лишь активные
сопротивления. При коммутации в таких
цепях токи и напряжения устанавливаются
мгновенно.
В радиотехнике и связи переходные процессы имеют первостепенное значение, так как длительность сигналов соизмерима со временем переходных процессов. Они влияют на форму сигналов. В некоторых схемах они нежелательны, поскольку являются причиной переходных искажений; в других – используются для получения сигналов заданной формы.
В автоматическом регулировании параметры переходного процесса определяют показатели качества системы (перерегулирование, время регулирования, декремент затухания и др.).
Во время переходных процессов на отдельных участках цепи могут возникать напряжения и токи, во много раз превышающие установившиеся значения. Это обстоятельство необходимо учитывать при разработке электрических и электронных схем.
Законы коммутации
Ток в индуктивности и напряжение на ёмкости в момент коммутации не могут изменяться скачком, а являются непрерывными функциями времени, т.е.

 Равенства (1.1) и
(1.2) выражают аналитически соответственно
первый и второй законы коммутации.
Равенства (1.1) и
(1.2) выражают аналитически соответственно
первый и второй законы коммутации.
В
схеме на рис. 1.2 а происходит коммутация
в цепи постоянного тока, содержащей
индуктивность. Ток в цепи до коммутации
 ;
ток в установившемся режиме после
окончания переходного процесса
;
ток в установившемся режиме после
окончания переходного процесса
 .
.
![]()
Н а
основании первого закона коммутации,
а
основании первого закона коммутации,

Н а
рис. 1.2 б показан постепенный, непрерывный
процесс установления тока в цепи после
замыкания ключа S.
а
рис. 1.2 б показан постепенный, непрерывный
процесс установления тока в цепи после
замыкания ключа S.

На рис. 1.3 поясняется второй закон коммутации.
В
схеме на рис. 1.3 а за время переходного
процесса напряжение на ёмкости непрерывно
изменяется от значения
 до
до
 (рис. 1.3 б).
(рис. 1.3 б).
В момент переключения в цепи при t=0 должен выполняться второй закон коммутации
 .
.
С
физической точки зрения законы коммутации
являются частными проявлениями общего
закона природы – закона непрерывности
энергии. Энергия магнитного поля,
запасённая в индуктивности
 ,
и энергия электрического поля, запасённая
в ёмкости
,
и энергия электрического поля, запасённая
в ёмкости
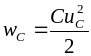 ,
не могут изменяться скачком. Действительно,
скачкообразное изменение
,
не могут изменяться скачком. Действительно,
скачкообразное изменение
 или
или
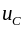 влечёт за собой скачкообразное изменение
влечёт за собой скачкообразное изменение
 или
или
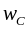 .
В этом случае мгновенные мощности в
индуктивности
.
В этом случае мгновенные мощности в
индуктивности
 в ёмкости
в ёмкости
 равны бесконечности, что лишено
физического смысла, так как реальные
источники энергии не могут развивать
бесконечно большую мощность. С другой
стороны, если допустить, что в момент
коммутации ток
(или напряжение
)
изменяется скачком, то напряжение на
индуктивности
равны бесконечности, что лишено
физического смысла, так как реальные
источники энергии не могут развивать
бесконечно большую мощность. С другой
стороны, если допустить, что в момент
коммутации ток
(или напряжение
)
изменяется скачком, то напряжение на
индуктивности
 (ток в ёмкости
(ток в ёмкости
 )
примет бесконечно большое значение, и
в цепи не будет выполняться второй (или
соответственно первый) закон Кирхгофа.
)
примет бесконечно большое значение, и
в цепи не будет выполняться второй (или
соответственно первый) закон Кирхгофа.
Заметим, что ток в ёмкости и напряжение на индуктивности не являются носителями энергии, поэтому законам коммутации не подчиняются и могут изменяться скачком.
Переходный, принуждённый и свободный процессы
Изучение переходных процессов сводится к исследованию и решению уравнений равновесия токов в узлах и напряжений в контурах, составленных применительно к их мгновенным значениям, т.е. в интегро-дифференциальной форме.
Рассмотрим пример подключения последовательного RLC-контура
(рис. 1.4) к источнику непрерывно изменяющейся ЭДС, заданной аналитически.
П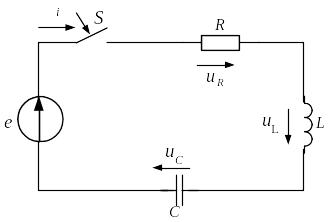 олагая
олагая
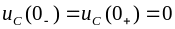 ,
для произвольного
,
для произвольного
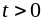 составим уравнение равновесия напряжений
в контуре
составим уравнение равновесия напряжений
в контуре
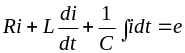 .
.
Ток
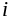 в уравнении (1.3) называется током
переходного процесса или переходным
током. После окончания переходного
процесса наступает принуждённый
(вынужденный) режим, который создается
в цепи источником ЭДС.
в уравнении (1.3) называется током
переходного процесса или переходным
током. После окончания переходного
процесса наступает принуждённый
(вынужденный) режим, который создается
в цепи источником ЭДС.
В случае постоянной, синусоидальной или любой периодически изменяющейся ЭДС принуждённый режим называют также установившимся.
С установлением принуждённого режима уравнение (1.3) примет вид
 , где
, где
 – принуждённый ток.
– принуждённый ток.
Вычитая из уравнения (1.3) уравнение (1.4) и вводя обозначение
 , получим
, получим
 .
.
Ток
 называется свободным током или током
свободного процесса.
называется свободным током или током
свободного процесса.
Уравнение (1.5) показывает, что переходный процесс в цепи можно рассматривать как суперпозицию (наложение) двух процессов - принуждённого, наступающего сразу после коммутации, и свободного, существующего только во время переходного процесса, т.е.
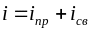 .
Физически существует только один ток
– переходный, и представление его в
виде двух составляющих упрощает расчёт
переходного процесса, сводящийся к
решению линейного неоднородного
дифференциального уравнения.
.
Физически существует только один ток
– переходный, и представление его в
виде двух составляющих упрощает расчёт
переходного процесса, сводящийся к
решению линейного неоднородного
дифференциального уравнения.
Ч астное
решение такого уравнения дает принуждённый
ток, общее решение однородного –
свободный ток. Тогда переходный ток
есть общее решение неоднородного
дифференциального уравнения.
астное
решение такого уравнения дает принуждённый
ток, общее решение однородного –
свободный ток. Тогда переходный ток
есть общее решение неоднородного
дифференциального уравнения.
В нахождении принуждённой и свободной составляющих тока или напряжения (интегрировании дифференциальных уравнений) и заключается расчёт переходных процессов классическим методом.
Порядок расчёта переходного процесса
Анализ переходного процесса в разветвлённой цепи начинают с составления системы уравнений для мгновенных значений токов и напряжений, используя любой подходящий для расчётов метод (контурных токов, узловых потенциалов, законов Кирхгофа и др.). Если требуется найти какой-либо один ток (или напряжение), то систему исходных дифференциальных уравнений путём исключения остальных переменных приводят к одному уравнению n-го порядка:
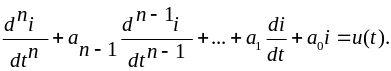 Принуждённая
составляющая
зависит от вида приложенного напряжения
– это либо постоянное, либо синусоидальное
напряжение; составляющую
находят обычными методами расчёта
установившегося режима после коммутации.
Принуждённая
составляющая
зависит от вида приложенного напряжения
– это либо постоянное, либо синусоидальное
напряжение; составляющую
находят обычными методами расчёта
установившегося режима после коммутации.
Физическая причина свободного процесса – несоответствие запаса электромагнитной энергии в реактивных элементах цепи в момент коммутации тому значению, которое должно быть в них после коммутации.
Свободный ток представляет общее решение однородного уравнения
 .Решение
уравнения (1.9) находят в виде
.Решение
уравнения (1.9) находят в виде
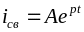 . Подставив
экспоненту
. Подставив
экспоненту
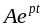 и её производные
и её производные
 в уравнение (1.9), после сокращения
получают алгебраическое уравнение
степени
в уравнение (1.9), после сокращения
получают алгебраическое уравнение
степени
 ,
которое называют х а р а к т е р и с т и
ч е с к и м у р а в н е н и е м:
,
которое называют х а р а к т е р и с т и
ч е с к и м у р а в н е н и е м:
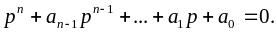 Каждый из n корней
уравнения (1.11) даёт линейно независимое
решение
Каждый из n корней
уравнения (1.11) даёт линейно независимое
решение
 ;
общее решение уравнения (1.9) представляет
линейную комбинацию этих решений. Вид
корней
;
общее решение уравнения (1.9) представляет
линейную комбинацию этих решений. Вид
корней
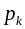 определяет характер свободного
процесса, его функциональную зависимость
от времени.
определяет характер свободного
процесса, его функциональную зависимость
от времени.
В частном случае, если корни характеристического уравнения вещественные и различные, выражение свободного тока имеет вид
 ,где
,где
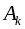 – постоянные интегрирования.
– постоянные интегрирования.
Другие варианты возможных решений для рассмотрены ниже в § 1.13.
Постоянные интегрирования в выражении (1.12) определяют из начальных условий – значений токов и напряжений в цепи при .
Прежде всего из законов коммутации (1.1) и (1.2) находят н е з а в и с и м ы е н а ч а л ь н ы е у с л о в и я (значения), которые справедливы только для тока через индуктивность и для напряжения на ёмкости. Значения остальных токов и напряжений при (з а в и с и м ы е н а ч а л ь н ы е у с л о в и я) определяют по независимым начальным условиям, используя законы Кирхгофа.
Отметим, что порядок дифференциального уравнения (1.8) (порядок цепи) равен общему числу индуктивностей и ёмкостей, для которых можно задать независимые начальные условия. Ввиду того, что решения для свободного тока (или напряжения) в любой ветви цепи имеют стандартную форму (1.10), а корни уравнения (1.11) зависят только от параметров цепи R, L, C, нет необходимости всякий раз составлять и обрабатывать дифференциальные уравнения. Расчёт переходного процесса рекомендуется вести в следующем порядке. Выбрать условно положительные направления токов в ветвях цепи. Записать для искомого тока общее решение в виде .
Найти
в установившемся режиме после коммутации.
Составить характеристическое уравнение
и найти его корни. Его можно записать
по виду дифференциального уравнения
(1.9), если последнее известно. Другой,
более простой способ его получения
состоит в том, что для цепи находят
комплексное входное сопротивление
 ,
в котором заменяют
,
в котором заменяют
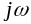 на
на
 ,
а затем приравнивают к нулю.
,
а затем приравнивают к нулю.
 можно составить относительно любой
ветви цепи, причём источник ЭДС следует
условно закоротить, так как его внутреннее
сопротивление равно нулю. По виду корней
характеристического уравнения записать
решение для свободного тока
(см. § 1.13). Определить независимые
начальные условия (1.1) и (1.2)
можно составить относительно любой
ветви цепи, причём источник ЭДС следует
условно закоротить, так как его внутреннее
сопротивление равно нулю. По виду корней
характеристического уравнения записать
решение для свободного тока
(см. § 1.13). Определить независимые
начальные условия (1.1) и (1.2)
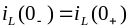 и
и
 и, используя их, найти зависимые значения
искомых токов (или напряжений) для
по законам Кирхгофа.
и, используя их, найти зависимые значения
искомых токов (или напряжений) для
по законам Кирхгофа.
Найти постоянные интегрирования. Записать окончательные выражения переходных токов и напряжений. Определить необходимые параметры переходного режима (постоянные времени, время переходного процесса, величину выбросов и др.).
Б илет
№ 16.2. Нелинейные магнитные цепи на
постоянном токе. Законы Ома и Кирхгофа
для магнитной цепи. Расчет магнитной
цепи с последовательным соединением
участков (прямая и обратная задачи).
илет
№ 16.2. Нелинейные магнитные цепи на
постоянном токе. Законы Ома и Кирхгофа
для магнитной цепи. Расчет магнитной
цепи с последовательным соединением
участков (прямая и обратная задачи).
Нелинейными называются цепи, параметры которых зависят от тока или напряжения.
Процессы в нелинейных цепях описываются нелинейными, алгебраическими и дифференциальными уравнениями, которые составляются на основе законов Кирхгофа. Для аналитического решения уравнений необходимо выразить аналитически характеристики всех нелинейных элементов цепи; от удачного выбора приближённых аналитических выражений характеристик зависит возможность аналитического решения задач.
Для анализа в нелинейных цепях часто используются графические и графоаналитические методы, они могут дать более точный результат, т.к. в них используются реальные характеристики нелинейных элементов, заданные в виде кривых, однако эти методы не позволяют устанавливать общие связи и проанализировать изменение характера процесса при изменении параметров цепи.
Рисунок.
Прямая задача: найти намагниченный ток I, при котором магнитный поток Ф в воздушном зазоре будет иметь заданное значение.
П ренебрегаем
магнитными потоками рассеивания.
ренебрегаем
магнитными потоками рассеивания.
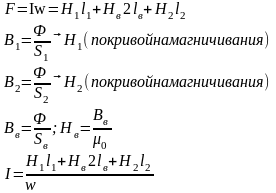
Обратная задача: требуется определить магнитный поток по заданному МДС. Эта задача не имеет прямого решения из-за нелинейной связи между магнитным потоком и намагничивающим током.

В практических расчетах нет необходимости строить всю кривую от 0 до заданной Hl, достаточно приравнять МДС к магнитному напряжению на участке с большим магнитным напряжением.

