15.2.Расчёт переходных процессов с помощью интеграла Дюамеля

Пассивный двухполюсник (рис. 3.2 а) включается на непрерывно изменяющееся напряжение 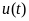(рис. 3.2 б). Требуется найти ток 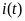в произвольной ветви двухполюсника после замыкания ключа.

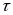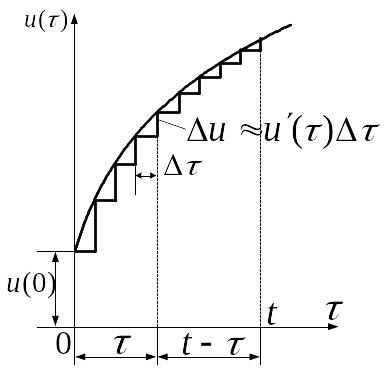
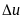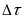Введём переменную , по которой будем вычислять интеграл Дюамеля, а через обозначим некоторый (текущий) момент времени, в который будем определять ток Заменим непрерывную кривую ступенчатой функцией и просуммируем составляющие искомого тока, вызванные начальным скачком напряжения и всеми последующими скачками , сдвинутыми на время друг относительно друга.

Напряжение вызовет ток 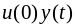, где 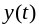- переходная проводимость, определённая для ветви, в которой вычисляется

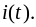
Элементарный скачок напряжения (рис. 3.2 б) может быть выражен через производную

ток, вызванный скачком в момент времени , равен

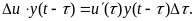Суммируя составляющие тока от всех скачков на интервале времени до 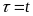и переходя от суммы к интегралу при получим выражение

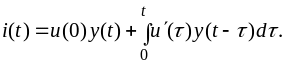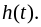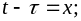
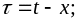
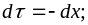
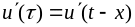
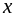Эта формула называется интегралом Дюамеля. С её помощью можно найти также и напряжение, если вместо использовать Если теперь провести замену переменной в подынтегральной функции (3.10): и вновь заменить на , то получим вторую форму интеграла Дюамеля

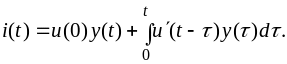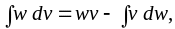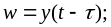
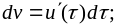
Интегрируя по частям выражение (3.10) обозначив при этом получим третью форму интеграла Дюамеля

.

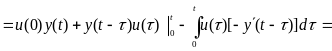
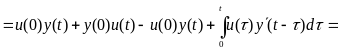
Наконец, интегрируя по частям формулу (3.11), найдём четвёртую форму интеграла Дюамеля 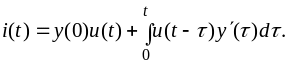(3.13)

При расчетах рекомендуется выбрать из формул (3.10) – (3.13) ту, которая даёт наиболее простое подынтегральное выражение. К примеру, в заданиях на курсовую работу [12], в которых внешнее воздействие 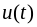задано в виде отрезков прямых, целесообразно использовать выражение (3.10), так как производная от линейной функции даёт постоянное число.

Пример 3.4

Напряжение в цепи (рис. 3.3 а) изменяется по линейному закону (рис. 3.3 б). Найти законы изменения тока в цепи и напряжение

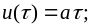
Выбираем формулу (3.10), в которой 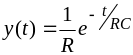(пример3.2);

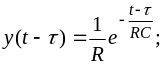
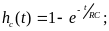
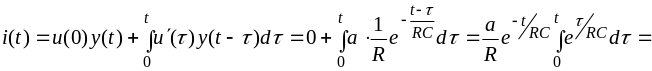
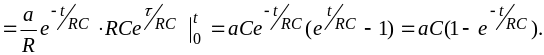(3.14)

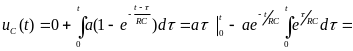
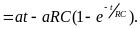
График тока приведён на рис. 3.3 в, 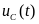- на рис. 3.9.

Р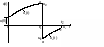 ассмотрим применение интеграла Дюамеля при сложной форме напряжения на входе пассивного двухполюсника (рис. 3.2 а). Напряжение задано в виде кусочно-непрерывной функции (рис. 3.4).

Требуется найти ток в одной из ветвей двухполюсника; переходная проводимость ветви известна.

При заданном внешнем воздействии (рис. 3.4) переходный процесс с помощью интеграла Дюамеля рассчитывают для трёх интервалов времени.

Для первого интервала времени

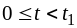
где 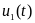- закон изменения в первом интервале без учёта скачка при .

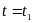Для второго интервала времени

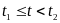
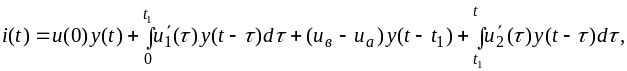
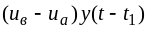где - закон изменения во втором интервале, слагаемое учитывает скачок напряжения (со знаком “минус”) в момент времени .

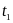Для третьего интервала времени

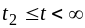
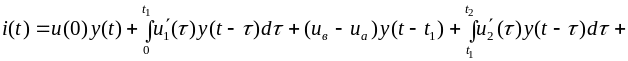
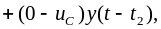
слагаемое 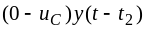учитывает положительный скачок напряжения в момент времени .

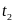П ример 3.5

На входе цепи (рис. 3.5) действует прямоугольный импульс (рис. 3.6 а). Найти напряжение на ёмкости и ток в цепи

Переходная функция по напряжению 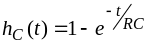(пример 3.2):

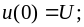
В первом интервале времени, 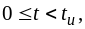заменив в формуле (3.10) на 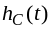, найдём

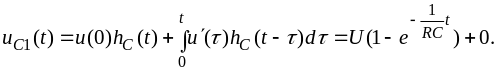
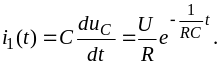
Во втором интервале времени, 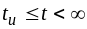найдём

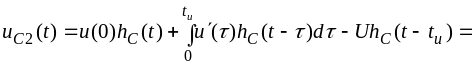
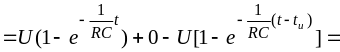
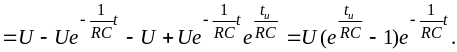
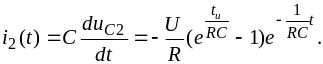
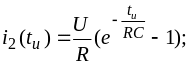
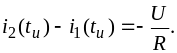
На рис. 3.6 б и в, качественно построены кривые и

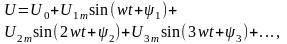
Единичная ступенчатая функция.

Единичная ступенчатая функция (синонимы: единичная функция, единичный скачок, единичное ступенчатое воздействие, функция включения, функция Хевисайда) изображена на рис. 3.1 а.

Математическая запись единичной ступенчатой функции

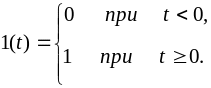
Единичная ступенчатая функции относятся к семейству разрывных или особых функций и используются для идеализированного представления сигналов. Эти сигналы, часто называемые в теории цепей единичный скачок напряжения и единичный импульс, обычно выбираются в качестве типового внешнего воздействия (возмущения), приложенного ко входу цепи (системы), при котором переходный процесс носит наиболее неблагоприятный характер. Кроме того, при помощи интеграла Дюамеля и интеграла свёртки они позволяют вычислить реакцию цепи на любое внешнее возмущение.

Переходные функции цепи. Импульсная переходная функция

Переходной функцией называют реакцию цепи на воздействие единичного скачка напряжения (или тока). Под реакцией понимают изменение во времени напряжения на любом участке цепи или тока в любой её ветви. Переходную функцию цепи определяют при нулевых начальных условиях. При воздействии на входе цепи скачка напряжения 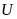ток 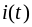в любой ветви можно представить в виде произведения напряжения на проводимость а напряжение на каком-либо участке цепи . Для единичного скачка напряжения, т.е. 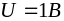при 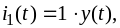где 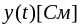- так называемая переходная проводимость;

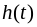- переходная функция по напряжению - это безразмерная величина, численно равная напряжению на каком-либо участке цепи, если на вход цепи подать постоянное напряжение в 1В. Переходные функции цепи и , называемые также переходными характеристиками, можно найти классическим или операторным методом

Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.

Действующие значения несинусоидального тока и несинусоидального напряжения. По определению, квадрат действующего значения тока I выражают через мгновенное значение тока iследующим образом:

Если ток

то

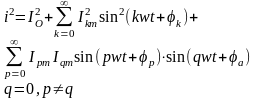
н о

П оэтому

Т ак как амплитуда k-гармоники тока I_km в 2 раз больше действующего значения тока k-гармоники I_k, то

Следовательно, действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От углов сдвига фаз  действующее значение тока не зависит.

А налогично, действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:

Активная и полная мощности несинусоидального тока.

П од активной мощностью P несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники:

Е сли представить напряжение u и ток i рядами Фурье:

П одставить эти ряды под знак интеграла и проинтегрировать, то можно получить

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.

П олная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока: S=U*I

где

Некоторые свойства периодических кривых, обладающих симметрией. На рис. 7.1 и 7.2 изображены три кривые, обладающие некоторыми специфическими свойствами. Кривая рис. 7.1а удовлетворяет условию f(x+л)=f(x).

Кривые, для которых выполнимо это условие, называют симмет­ричными относительно оси абсцисс. Если кривую рис. 7.1а, сместить по оси х на полпериода и зеркально отразить относительно оси х, то полученная кривая совпадает с кривой f(х).

При разложении таких кривых в ряд Фурье отсутствуют посто­янная составляющая и четные гармоники, т. е. равны нулю коэффи­циенты А₀ = А'₂=А"₂ = А'₄ = А''₄ =… =0.

Поэтому кривые типа кривой рис. 7.1а ,раскладывают в ряд f(x)= А'₁sin(x)+А"₁cos(x)+ А''₃sin(3x)+ А''₃cos(3x)+…

Каждое слагаемое этого ряда удовлетворяет условию -f(x+ л) = f(x), например -sin(x- л)=sin(x).

Кривая, подобная кривой рис. 7.1, б, обладает симметрией отно­сительно оси ординат и удовлетворяет условию -f(-x)= f(x).Если кривую, лежащую левее оси ординат, зеркально отразить относительно оси ординат, то полученная кривая совпадает с кри­вой, лежащей правее оси ординат. При разложении таких кривых в ряд Фурье отсутствуют синусные (А'₁=А'₂=A'₃=...=0) состав­ляющие, т. е. присутствуют лишь косинусные и постоянная состав­ляющие.

Таким образом, кривые типа кривой рис. 7.1б, можно разложить в ряд f(x) =A₀+A"_lcosx+A"₁cos2x+A"₃cos3x+ Кривые типа кривой рис. 7.2 удовлетворяют условию -f(-x)= f(x), их называют кривыми, симметричными относитель­но начала координат. Разложение их в ряд Фурье имеет такой вид: f(x) = А'₁sin(x)+А'₂sin(x)+ А'₃sin(3x)+…