14.2) Нелинейные резистивные цепи постоянного тока. Графические методы расчета. Метод пересечений. Метод эквивалентного генератора. Итерационный метод.

Нелин. Эл. Цепь – цепь, параметры которой зависят от тока или напряжения.

Процессы в нелинейных цепях описываются нелинейными алгебраическими и дифф.-ми урав., которые составляются на основании законов Кирхгоффа.

Для аналит. решения уравнений необходимо выразить аналит. хар-ки всех нелинейных элементов цепи. От удачного выбора приближенных аналит. выражений характеристик зависит возможность аналит. решения задач. Для анализа процессов в нелин.эл.цепях часто используются графические или графо-аналит. методы. Эти методы могут дать более точный результат, т.к. в них используются действительные характеристики нелинейных элементов, заданных в виде кривых. Однако эти методы не позволяют устанавливать общие связи и проанализировать изменение характера процессов при изменении параметров цепи. Часто используются приближенные методы. Широко применяются ЭВМ для решения нелинейных задач.

Г рафо-аналит методы целесообразны применять для решения задач, в которых хар-ки нелин. элементов может быть представлены в виде кусочно-линейно. При этом на каждом из линейных участков функции задача решается как линейная, и определяются координаты точек перехода с одного линейного участка на другой(углы отсечек).

Применение аналит. методов расчета требует аппроксимации характеристики нелинейного элемента какой-либо простой функцией.

Широко применяется:

• Метод гармонического баланса;

• Метод гармонич. линеанизации;

• Итерационный метод.

Метод пересечений.

Последовательная цепь разбивается на две части и на одном графике в одинаковых масштабах строятся ВАХ обеих частей. Т.к. обе части соединяются одна с другой, то напряжения и токи в месте их соединения должны быть равны. Это условие удовлетворяется только в режиме отображаемом точкой пересечения характеристик частей цепи.

Примеры нелинейных резисторов:

ВАх ламп накаливания:

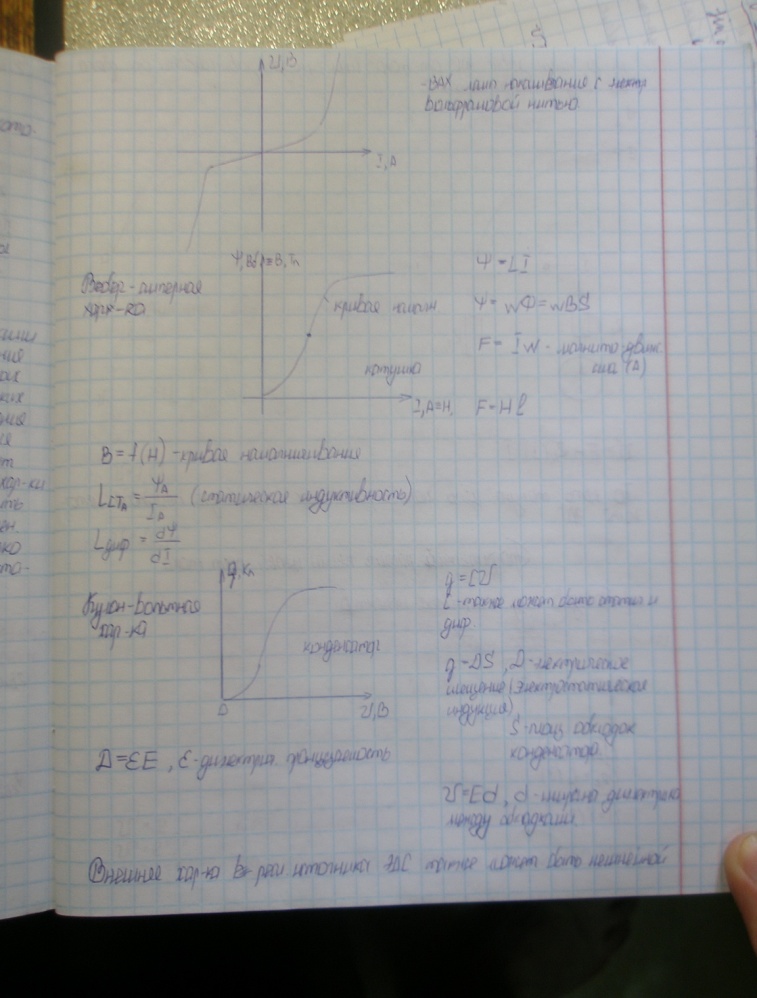
Вебер – амперная характеристика:

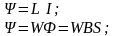
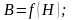
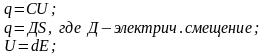
Внешняя характеристика реального источника ЭДС также может быть нелинейной из-за нелинейной зависимости ЭДС от тока или зависимости тока от его внутреннего сопротивления.

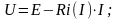
Такую цепь можно рассматривать как нелинейную при постоянном источнике ЭДС.

Графич. расчет нелинейных цепей постоянного тока.

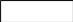
1. последовательное соединение нелинейных элементов.

R1

R2

.

Дано:Ur1=f1(I), Ur2=f2(I).

Найти: U=f(I)-?

U=U1+U2;

ad=ab+ac.

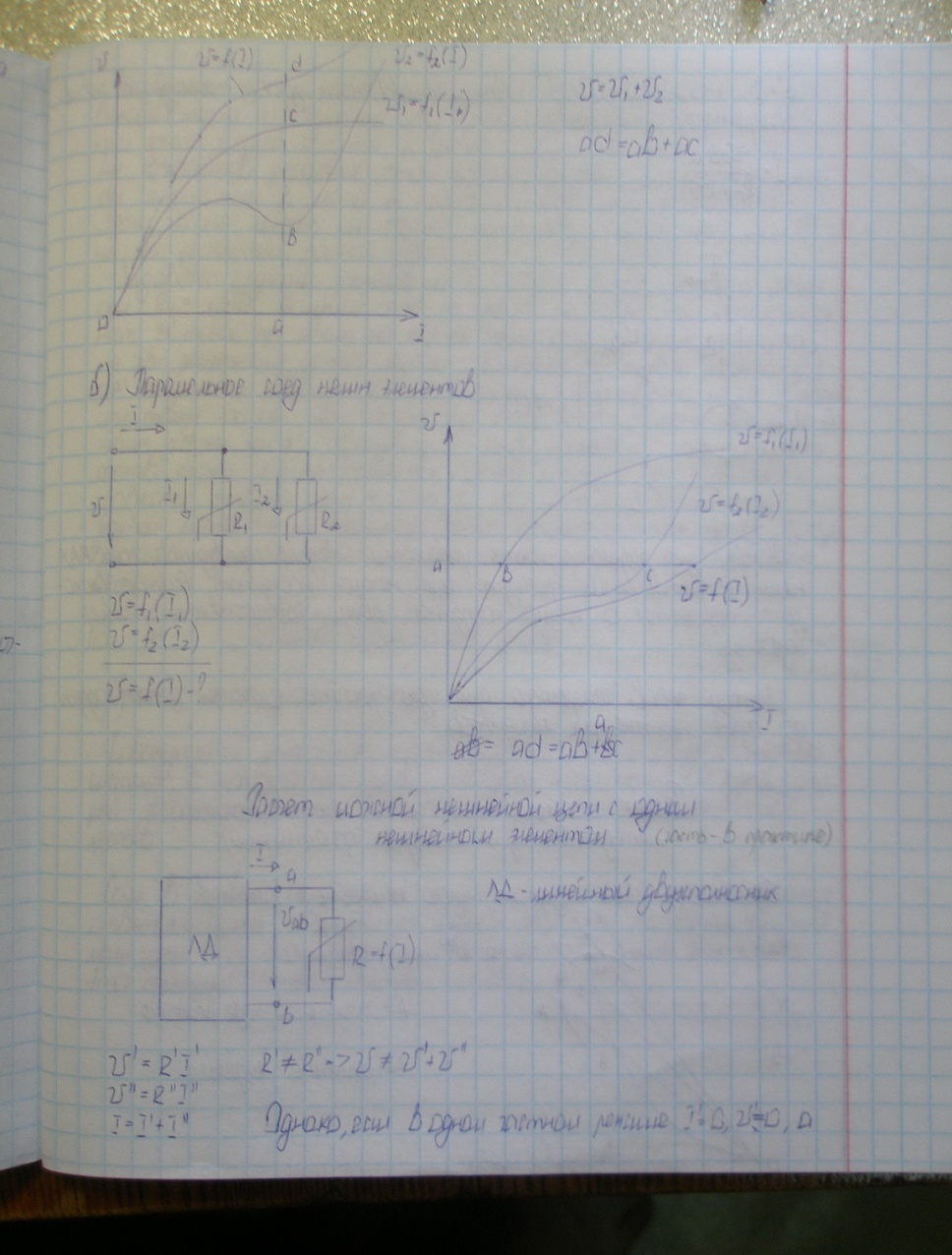
2. Параллельное соединение нелин. элементов.

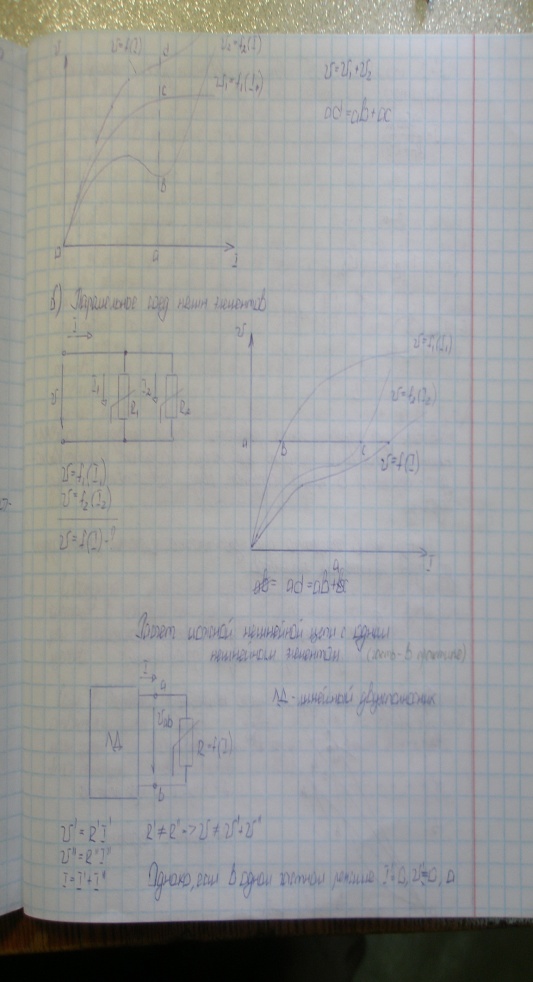
3. Расчет сложной нелин. цепи с одним нелин. элементом.

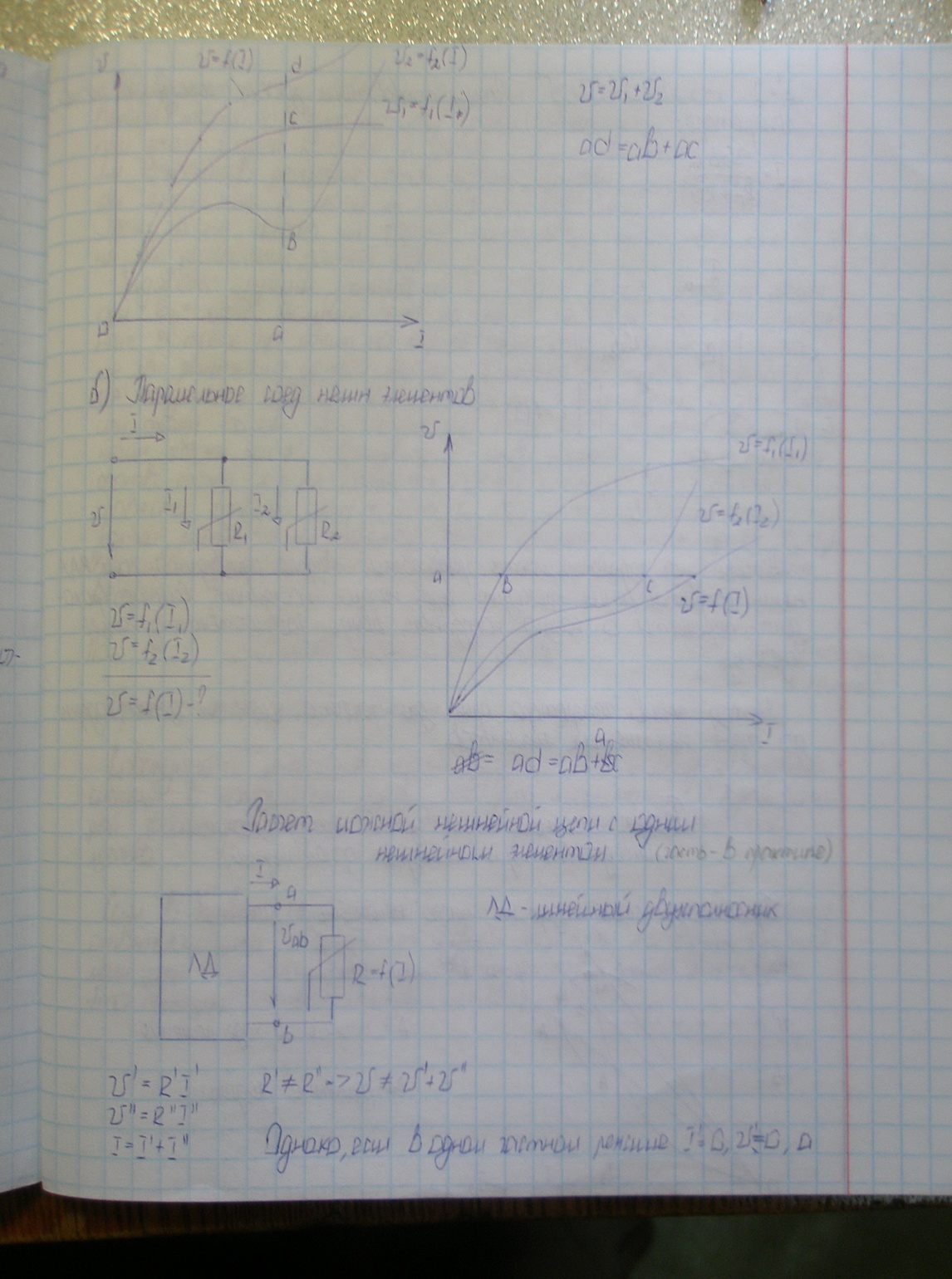
ЛД – линейный двухполюсник.

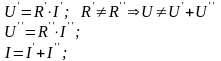
Однако, если в частном режиме , а

Этим требованиям удовл. теорема об эквивалентном генераторе.

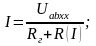
Дальше задача решается графически. Задача справедлива, если ВАХ нелин. сопротивления проходит через начал координат. Если не проходит – перенести в начало координат, введя ЭДС соответствующего сдвигу. Метод экв. генератора применяется для расчета сложных цепей, содержащих до трех нелинейных элементов.

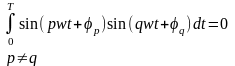
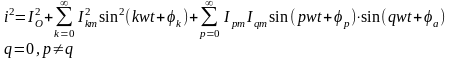
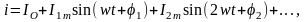
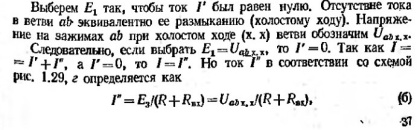
Итерационный метод

Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.

Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.

Метод простой итерации

1.Исходное нелинейное уравнение электрической цепи , где -искомая переменная, представляется в виде .

2. Производится расчет по алгоритму  где - шаг итерации. На интервале между приближенным и точным значениями корня должно выполняться неравенство . 1.Начальное приближение  обычно находится из уравнения  при пренебрежении в нем нелинейными членами.

2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка

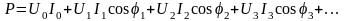
итерационные формулы имеют вид  ;

.

3. При решении системы уравнений сходимость обычно проверяется в процессе итерации.

Билет № 15:1.

Действующие значения и мощности при периодических несинусоидальных напряжениях и токах; коэффициенты характеризующие форму несинусоидальных периодических кривых.

Действующие значения несинусоидального тока и несинусоидального напряжения. По определению, квадрат действующего значения тока I выражают через мгновенное значение тока iследующим образом:

Если ток

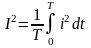
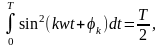
то

но

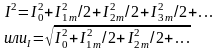
Поэтому

Так как амплитуда k-гармоники тока I_km в 2 раз больше действующего значения тока k-гармоники I_k, то

Следовательно, действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От углов сдвига фаз  действующее значение тока не зависит.

Аналогично, действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:

А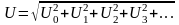 ктивная и полная мощности несинусоидального тока.

П од активной мощностью P несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники:

Если представить напряжение u и ток i рядами Фурье:

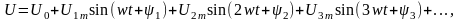
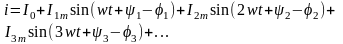
Подставить эти ряды под знак интеграла и проинтегрировать, то можно получить

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.

Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока: S=U*I

г де

Коэффициенты характеризующие форму несинусоидальных периодических кривых

1.

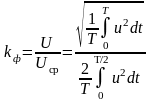
2.

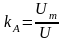
3.

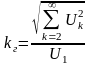
4.