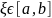- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
Пусть ф-ция y=f(x) задана табл. Значений для конечного множества Х
Такая таблица м.б. построена в рез-те наблюдений некоторого процесса, если же необходимо найти значение ф-ии f(x) для некоторого промежуточного значения аргумента, то строит ф-ию φ(х), достачно простую для вычислений, кот. в заданных точках х0, х1 .. хn принимают значение f(x0)… f(xn), а в остальых точках некотрого отрезка [a,b] функция φ(х) с той или иной степенью точности только приближает f(x). Отрезок [a,b] принадлежит области определения f(x). И в дальней шем при решении задач вместо f(x) будет использоваться φ(х).
Задача
построения такой функции φ(х) наз.
задачей интерполирования, а функция
φ(х) наз интерполяционной. Чаще всего
в качестве интерпол-ной функции берут
алг-ий многочлен n-ой
степени. К интерполированию прибегают
и тогда, когда фун-ция f(x)
задана аналитическим выражением с
помощью которой можно вычислить ф-цию
f(x)
в любой точке отрезка из области
определения f(x).
Но вычисление f(x)
м.б. соприжено с большим объёмом
вычислительных работ. Если же нужно
вычислить ф-цию f(x)
для большого кол-ва значений аргументов,
то тоже прибегают к интерполированию,
т.е. вычисляют f(x)
в нескольких точках: f(xi),
i=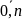 .
Далее по этим значниям строят φ(х),
а остальные значения функции f(x)
уже находятся в с помощью φ(х), кот проста
для вычислений. В дальнейшем в качестве
такой функции φ(х) мы будем брать алг-ий.
многочлен n-ой
степени. В этом случае интерполирование
будет наз-ся алгебраическим:
.
Далее по этим значниям строят φ(х),
а остальные значения функции f(x)
уже находятся в с помощью φ(х), кот проста
для вычислений. В дальнейшем в качестве
такой функции φ(х) мы будем брать алг-ий.
многочлен n-ой
степени. В этом случае интерполирование
будет наз-ся алгебраическим:
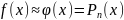 ,
причем f(xi)=Pn(Xi),
i=
.
А в остальных точках отрезка [a,b]
,
причем f(xi)=Pn(Xi),
i=
.
А в остальных точках отрезка [a,b]
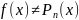 .
В дальнейшем обозначаем через Rn(x)
разницу f(x)
– Pn(x),
где Rn(x)
– ошибка от замены функции
.
В дальнейшем обозначаем через Rn(x)
разницу f(x)
– Pn(x),
где Rn(x)
– ошибка от замены функции
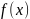 многочленом
многочленом
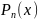 .
Или же
.
Или же
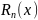 наз остаточным членом интерполирования,
наз остаточным членом интерполирования,
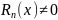 (погрешность метода).
(погрешность метода).
Двух различных интерполяционных многочленов степени n для ф-ции f(x) сущ-ть не может, т.е для f(x) сущ-ет единственный интерполяционный многочлен n-ой степени.
Интерполяционный
многочлен Лагранжа: Требуется
построить интерпол. Многочлен
в степени n
для ф-ии f(x),
кот в точках x0,
x1…
xn
(в узлах интерполяции) прин. Знач. y0,
y1…
yn.
Для построения используем фундаментальный
многочлен Qn(x):
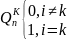
Тогда
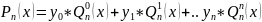 .
Легко увидеть что
.
Легко увидеть что
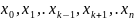
являются
корянми фундаментального многочлена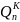 (x).
Т.о.
(x).
Т.о.
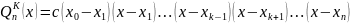 ,
где с- максимальный определитель из
условия:
,
где с- максимальный определитель из
условия:

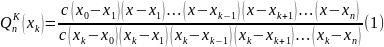
Тогда
 (2)
(2)
Фундаментальные
многочлены
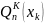 – n-ой
степени значит и сам многочлен
– n-ой
степени значит и сам многочлен
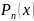 - тоже n-ой
степени.
- тоже n-ой
степени.
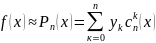 (3)
(3)
Имеем
(2) - Интерполяционный
многочлен Лагранжа. (1) – коэф. Лагранжа.
(3) - Интерпол-ная формула Лагранжа.
формулы 1-3 можно записать компактно,
если воспользоваться след обозначениями:
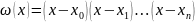 ;
;
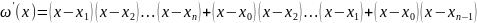 .
Тогда в точке
.
Тогда в точке
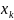
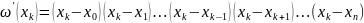
Справедливо
записать :
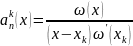 ;
;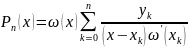 :
:
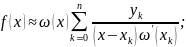 многочлен
совпадает
с
многочлен
совпадает
с
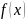 в точках
,
i=
, а в остальных точках отрезка [a,b]
в точках
,
i=
, а в остальных точках отрезка [a,b]
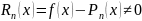 .
Справедлива теорема (для оценки
остаточного члена): если
в промежутке [a,b]
имеет непрерывные производные до (n+1)
порядка включает, то остаточный член
интерполяции
.
Справедлива теорема (для оценки
остаточного члена): если
в промежутке [a,b]
имеет непрерывные производные до (n+1)
порядка включает, то остаточный член
интерполяции