15. Метод квадратного корня решения слау.

Метод применяется, если м-ца А-системно симметрическая, т.е. А=А^т (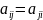 ). Известно, чтоA–симметрич. А=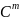 DС, где С-некая верхняя треуг м-ца.

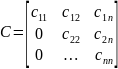, где С_ii>0

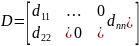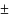,d_ii= 1

Тогда вместо сист Ax=b (1) будем иметь С^тDCx=b (2). Если обозн T=C^TD, то зависимость ТСх=b, кот на практике заменяется след системой:

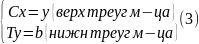
Заменив (1) на (3) мы свели решение системы к решению системы с треуг матрицами (это ускоряет процесс нах-ния х методом Гаусса).

Матрица Т=С^тD=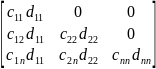 . Отсюда матр А=ТС, поютому для того чтобы найти эл-т a_ij надо i-тую строку мат-цы Т умножить на j-тый столбец м-цы С:

a_ij=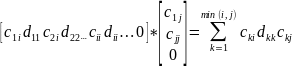 (4), если i=j.

1) если j=1, i=1, то a₁₁=c₁₁²d₁₁, т. е. d₁₁=sign(a₁₁), c₁₁=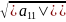

2) если i=1, 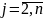, то a_ij=c₁₁d₁₁c_{1j ⟹} ,

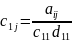Т. о. мы нах всю первую строку ма-цы С.

3) Если i=j, то из (4) мы получим a_ii=c_1i²d₁₁+c_2i²d₂₂+..+c_ii²d_ii

Отсюда c_ii²d_ii= a_{ii 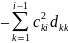⟹} d_ii=sign(a_ii ). Получим

.

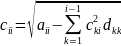Также из (4) можно получить зависимость 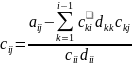, for i j

Из получ ф-л видно что м-ца С явл Δ, как и м-ца Т. Т. о. сис-а Ax=b свод. к сис-е ур-ий: 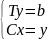с треуг м-цами.

Схема реализ м-да квадр корня в случае, когда м-ца А полож опред.

В данной ситуац у м-цы А главн миноры полож. ⟹ в этом случ м-ца Д совпад с Е, а значит получ ф-лы упростяться. Т.о. Ax=b сведется

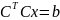
Из (*) y₁=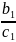 , 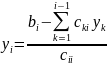для i>1

Из (**) x_n=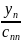 , x_i==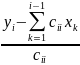 для i<n

16. Метод простой итерации решения СЛАУ Покажем как применяется принцип сжатых изображений к исследованию скорости сходимости и самой сходимости итерационных процессов решения систем уравнений. Пусть дана система вида: Х=Вх+b (1) где B=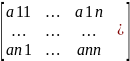 X= b= Правую часть уравнения (1) обозначим через Ф(х), тогда Ф(х) можно уже рассматривать как отображение пространства Rn Rn, где 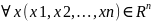; ; 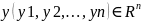; ; 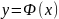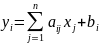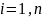(2 – координаты 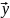). Решение уравнения (1) таким образом сведется к отысканию неподвижной точки отображения Ф. Для того чтобы отображение Ф имело неподвижную точку – нужно чтобы Ф было сжатием. Если покажем, что Ф – сжатие, тогда имеет в пространстве 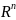единственную неподвижную точку х* и к ней будет сходится итерационный процесс: xn+1=Ф(xn), xn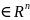 ; x(n+1)=Bx(n)+b (3). В координатной форме метод (3) запишется: xi(n+1) =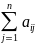 (n) + bi, (4). Определим при каких же условиях Ф будет сжатием. Убедимся, что ответ зависит не только от Ф, но и от выбора метрики. Рассмотрим первую метрику пространства - кубическую. 1) 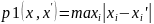, где х=(x1, x2,…, xn), х=(x1 , x2 ,…, xn ). 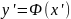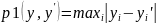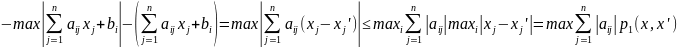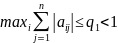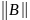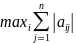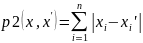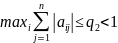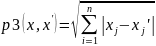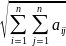; - следовательно, чтобы Ф было сжатие ; 1 = (5) 2) Рассмотрим метрику октаэдрическую: аналогично случаю 1) мы можем показать, что Ф будет сжатием, если: 2 = (6) 3) Для сферической метрики: 2 ; 3 = 2 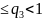(7) Таким образом если выполняется одно из условий (5)-(7) то Ф – сжатие. И по принципу Банаха для отображения Ф в пространство существует единственная неподвижная точка х* (х*, …,хn*) к которым сходится итерационный процесс (3)/(4). -> Доказали Теорему. Теорема: если для матрицы В из уравнения (1) выполняется одно из условий l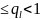 , l=1,3 то система линейных алгебраических уравнений (1) имеет единственное решение х*, которое может быть получено по формуле (3) как предел последовательности, начиная с некоторого х0. Причем скорость сходимости процесса (3) определяется следующим соотношением: 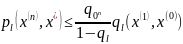. Пусть дана система Ах=b. Домножим на -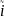 обе части: х - Ах=-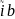 +x; x= Ах - +x; x(n+1)=(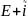 A)xn - (*) Чтобы процесс (*) сходился -> =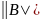 <1. Очевидно, что в итерационный процесс до конца выполнения просчета шага n+1 должны сохранятся и значения n-шага. Этим недостатком не владеет метод Зейделя, который является модификацией метода простой итерации. 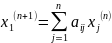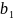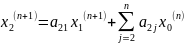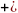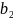Метод Зейделя: + ; 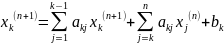Предлагаемый метод позволяет сразу же использовать при вычислении координат вектора х(n+1) уже найденные его предыдущие координаты. Условие сходимости и метода Зейделя и метода простой итерации одинаковы. Области сходимости у этих методов не всегда совпадают, а если совпадают то скорость Зейделя > скорости итерации.

17. Решение систем нелинейных ур-ий

Систему нелинейных уравнений можно кратко записать в векторном виде f(x)=0 или в коор. виде:

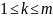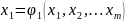
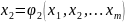
f_k(x₁,x, … x_m)=0, . Такие системы решаются только итер. Методами. Для такой сис-мы исп м-д простой итерации. Для этого приводят сис-му к виду: 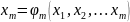(15.1)

Для ее записи в m - мерном числовом пространстве R_m введем два вектора: один из них х для изображения совокупности неизвестных (х₁,х₂,...х_m), второй 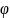будет обозначать совокупность значений функций (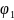 , ,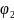... 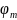). Система запишется в краткой векторной форме х = (х). Пусть как-то выбрано начальное приближение к решению х⁰ =(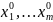 ) Все следующие приближения будут находиться по правилу итераций xⁿ⁺¹ =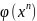 . Для выяснения условий, достаточных для сходимости последовательности приближений хⁿ (n = 0,1,...,) применим теорему Банаха о сжимающих отображениях. Для этого нужно в R_m ввести метрику.

1. Случай кубической метрики

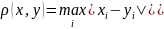
В шаре 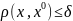возьмем две произвольные точки х(х₁,х₂,...х_m) и y(y₁, y₂, … y_m) оценим изменение функции :

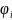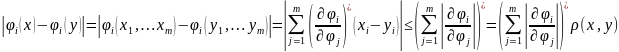
Звездочкой у скобок отмечено то, что значение функции, стоящей в скоб­ках, должно быть взято в некоторой точке отрезка прямой, соединяющего х и у. Чтобы найти оценку изменения, не зависящую от i и положения точек х и у, заменим последнюю из скобок ее максимальным значе­нием по х и i. Тогда получим

Отсюда видно, что в качестве числа q может быть взята величина

q=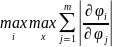

Все это позволяет сформировать теорему о сходимости итерационной последовательности в случае кубической метрики.

Теорема 15.1

Пусть

1) функции 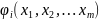определены и непрерывно дифференцируемы в области области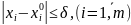

2) в этой области

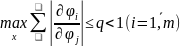
3) начальные приближения неизвестных удовлетворяют неравенствам

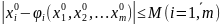
4) для чисел , q и М выполняется условие

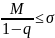
Тогда система (15.1) в области 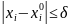имеет решение (x₁^*, x₂^*… x_m^*) и к нему сходиться итер. посл-ть приближений (x₁ⁿ, x₂ⁿ… x_mⁿ)

2) Скорость сходимости м.б. охарактеризована нерав-м:

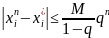, (i= )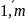

2. Случай октаэдрической метрики

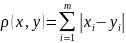
3. Случай сферической метрики

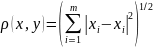
Сходимость метода линейная. Сами вычисления просты, но сложно найти такую систему х=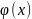 , которая была бы эквивалентна исх.сис-ме f(x)=0 и одновременно обеспечивала бы сходимость.

18. Надо решить сис-му нелин. ур-ний

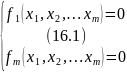
Рассмотрим n - мерное векторное пространство Rm, x=(x1,…xm). Введем вектор - функцию f(x)=(f1(x), f2(x),… fm(x)), тогда система (16.1) запишется в виде f(x)=0 (16.2)

Пусть известно некоторое исходное приближение х° = {х1°,х2°,..., хn°} к решению системы х* = (х1*,... хm*). Для выделения главной линей­ной части из системы (16.2) удобно рассмотреть не точное решение х*, а вектор-погрешность х* - х° = (х1* - х10, … хm* -хm°)= = (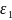 ,..., 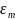). Уравнение для получится, если в равенстве f(х*)=0 заменить х* на х° + , т.е. f(х° + )= 0. Предполагая все составляющие вектора малыми величинами, выделим в системе (16.1) главную линейную часть. Для этого рассмотрим уравнение любого номера fi(х° + )=0 и разложим fi в ряд Тейлора по степеням погрешности 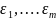и сохраним в разложении линейную часть, отбросив все члены более высокого порядка. После этого получится линейная система уравнений относительно погрешностей, приближенно заменяющая систему (16.1).

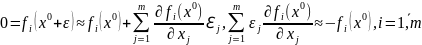
Решая ее относительно 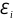, например, методом Гаусса, мы получим приближенные значения для например, 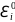, 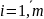Мы улучшим исходные значения неизвестных xi0 ,если к ним прибавим , т.е.

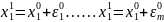
Новые значения х1m аналогичными вычислениями могут быть тоже улучшены и т.д. В результате для каждого значения хi* получится последовательность приближений хin такая, что каждое следующее приближение хin+1 будет находиться из линейной системы по предыдущему приближению хin:

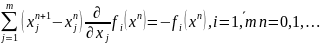
Рассмотрим матрицу Якоби системы функций fi, i=1,m

(16.4)

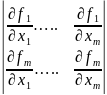
Значение ее при х = хn есть матрица системы (16.4). Система будет иметь единственное решение, если ее определитель отличен от нуля 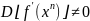. Итак, метод Ньютона сходится, если в достаточно малой окрестности

корня 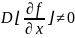, причем сходимость квадратичная. Вычисления по

методу Ньютона несколько сложнее, чем при простых итерациях, ибо на каждом шаге надо находить матрицу производных и решать систему линейных уравнений. Поэтому в некоторых учебниках рекомендуют вычислить матрицу производных только на начальной итерации и использовать ее во всех остальных итерациях.