
- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
13. Метод Гаусса.
Пусть дана система ур-й:
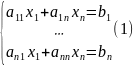
Метод
Гаусса состоит в том, что система (1) с
произвольной матрицей А приводится к
системе
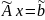 (3), где
(3), где
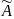 –
верхняя треугольная матрица.
–
верхняя треугольная матрица.
Из сис-мы (3) из посл-го ур-я нах xn , из предпосл-го xn-1 и т д. Сведение сис-мы (1) к к сис-ме (3) наз прямым ходом метода Гаусса, а нах-ние xn , xn-1, …, x1 обратным ходом.
При
вычислении по этому методу велика
вер-ть ошибок.
Поэтому
вводят контр столбец
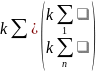 ,
где
,
где
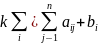 .
Эл-ты контр столбца преобр по тем же
ф-лам что и эл-ты строк матрицы, а затем
провер рав-ство суммы эл-тов преобр-х
строки и контр эл-та. Они должны совп с
точностью до 1-2 единиц последнего
разряда. При необходимости т/ой же
контроль и в оьратном ходе м-да Гаусса
м проводить.
.
Эл-ты контр столбца преобр по тем же
ф-лам что и эл-ты строк матрицы, а затем
провер рав-ство суммы эл-тов преобр-х
строки и контр эл-та. Они должны совп с
точностью до 1-2 единиц последнего
разряда. При необходимости т/ой же
контроль и в оьратном ходе м-да Гаусса
м проводить.
Mетод Гаусса с выбором главного элемента решения СЛАУ.
Сначала выбираем ур-е, содержащее наибольший по абсол величине коэф-т, и делим данное ур-ние на этот коэф. Если этот эл-нт стоит при х1,то при х1 получится 1 и с пом этой 1 исключим перем х1 из всех ост ур-ний. Если же гл эл-нт не при х1 , то для удобства его надо переставить в первую строку в первый столбец.
Далее, оставляя неизменным ур-ние с гл эл, ищут наиб по абс величине коэф в ост ур-ниях, делят на него ур-ние, в кот нах-ся, и искл-ют из ост ур-ний соотв-щее неизвестное. В рез-те получ матрица диагонального вида.
Вычисление определителя.
Идея
способа Гаусса посл-ного исключения
неизв перем в системе ур-й также м б
перенесена на задачу выч-ния определителя,
только здесь она переходит в способ
послед-го понижения порядка n
опр-ля. Рассмотрим
схему единственного деления. Пусть дан
определитель
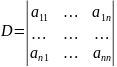
Выберем
ведущий элемент первого шага
преобразований. Он д б отличным от 0;
чтобы избежать сильного разброса в
порядках чисел, за него принимают либо
наиб по модулю элемент опр-ля D,
либо
наиб эл-нт в избранной строке или
избранном столбце. Выполняя т. о.
перестановку строк и столбцов, можно
считать, что за ведущий элемент принят
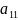 .
Вынося
из
первой строки (столбца) за знак D, приведем
определитель к виду
.
Вынося
из
первой строки (столбца) за знак D, приведем
определитель к виду
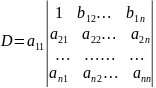
Умножая
первую строку последовательно на
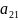 ,
,
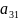 ,
…,
,
…,
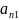 и вычитая из второй, третьей и т.д.
строк, получим
и вычитая из второй, третьей и т.д.
строк, получим
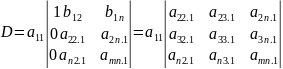
Этим
мы понизим порядок определителя на
единицу и можем перейти ко второму шагу
преобразований, применяя к полученному
порядку n-1 такие же преобразования.
Выполнив все n
шагов, найдем определитель D как
произведение ведущих элементов:
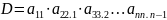
14. Обращение матриц и уточнение приближенной обратной матрицы.
Пусть дана невырожд (неособен) матрица, т е детерминант А 0.
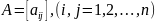 .
Для невырожд матрицы всегда
обратная:
.
Для невырожд матрицы всегда
обратная:
1)
А-1=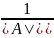 ,
где Aij=(-1)i+j∙Mij.
Здесь нам придется выч-ть один опр-ль
n-го
порядка и n2
опр-ль (n-1)-го
порядка.
,
где Aij=(-1)i+j∙Mij.
Здесь нам придется выч-ть один опр-ль
n-го
порядка и n2
опр-ль (n-1)-го
порядка.
2)
Если обозн через x=A-1,
то обр матр будет решением матр-го ур-я
Ax=E,
т е
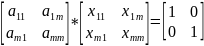 .
Решая
данное ур-ние, будем иметь дело с
n-системами
ур-ний, сод-щих n2
переменных
.
Решая
данное ур-ние, будем иметь дело с
n-системами
ур-ний, сод-щих n2
переменных
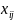 .
.
3)
Составим расшир м-цу и с помощью преобраз
получ
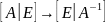 .
.
В
рез-те
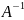 будет
получено неточно (из-за округлений), т
е получим
будет
получено неточно (из-за округлений), т
е получим
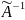 .
Необходимо уточнить
,
так чтобы выполнялось нер-во:
.
Необходимо уточнить
,
так чтобы выполнялось нер-во:
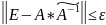 .
Где -заданная точность.
.
Где -заданная точность.
Для уточнения эл-тов исп итерационный процесс:
Дn=Дn-1+ Дn-1∙Fn-1. (1)
Fn-1=Е-А∙ Дn-1 (2)
Д0= .
Если
будет вып-ся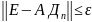 ,
то Дn
выберем
в качестве решения задачи.
,
то Дn
выберем
в качестве решения задачи.
