
- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
Пусть f(x)- непрерыв. ф-ция и надо нам решить ур-ние f(x)=0.
Число
х=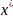 наз. решением ур-ния1, если f(
наз. решением ур-ния1, если f(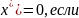 f(x)-непрерыв.
на [a,b],
и в то же время f(a)*f(b)<0,
то на этом отрезке существует
хотя бы 1 корень.
f(x)-непрерыв.
на [a,b],
и в то же время f(a)*f(b)<0,
то на этом отрезке существует
хотя бы 1 корень.
Отделить корни ур-ния значит найти отр. в кот. нах. только 1 корень ур-ния. Для отдел. корней ур-ния 1 исп. теорема.
Критерий
Если f(x) непрерыв. и монотонна на [a,b] и f(a)*f(b)<0, то на данном отрезке существует единств. Корень ур-ния 1.
Отделить корни также можно и графически: найти т. пересеч. графика у= f(x) с осью ОХ.
Самый лучший способ отделения корней- метод Штурмана.
Дихотомия (деление отрезка пополам)
Требуется решить ур-ние 1, где f(x)-непрерыв. ф-ция.
Пусть
каким-то образом мы определ. отрезок
[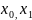 ],
что выполн. f(
],
что выполн. f(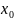 )*f(
)*f(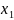 )<0.
Далее произведем деление
)<0.
Далее произведем деление
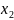 =
=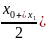 .
Из 2-х получ. отрезок: выберем тот, на
концах кот. f(x)
разного знака.
.
Из 2-х получ. отрезок: выберем тот, на
концах кот. f(x)
разного знака.
Выбр. отрез. аналог. делим пополам. Если нам надо получ. корень с опред. точн. , то мы будем продолж. деление до тех пор, пока длина получ. отрезка не станет=2*ε. Тогда длина получ. отр. не станет=2*ε. Тогда длина получ. отр. и будет реш. с точн. ε. Дихотомия проста и надежна в исп. она всегда сход. к простому корню для любой непрерыв. ф-ции в т. ч. и недифференцир. Дихотомия устойчива к округл. Скорость сходимости дихот. невелика: за одну итерацию точность увелич. ≈ в 2 раза.
Теорема (принцип Банаха)
Пусть
R-
полное метр. пр-во. Если отобр. f:
R→R
явл. сжатием, то для него существ.
единств. неподвиж. точка, кот. явл.
пределом послед.
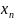 получ. по ф-ле:
получ. по ф-ле:
 =f(
),
€R.
=f(
),
€R.
Док-во:
1)
Рассм. метрику
(
,
)=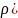 (
(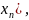 f(
f(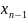 ))≤α
(
))≤α
(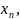 )≤
)≤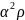 (
,
(
,
 )≤…≤
)≤…≤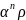 (
(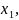 ),где
0<α<1.
),где
0<α<1.
2)
Возьмем k<l
(k,l-члены
послед.):
(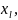
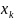 )≤
(
)≤
(
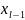 )+
(
)+
(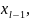 )≤
(
)+
(
)≤
(
)+
(
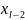 )+
(
)+
(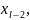 )≤
(
)+
(
)+…+
(
)≤
(
)+
(
)+…+
(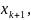 )≤
+
)≤
+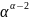 +…+
+…+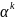 )
(
)=
(
)
(
)=
(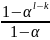 )
)
(
)≤ (
)→0
(
)→0
Т.о. мы получаем, что - фундаментально.
3)Т.к. R-полное метр. пр-во, то в нем всякая фунд. послед. сходится т.е. → €R.
Покажем, что - неподвиж. точка отображ. f, т.е. имеет место след. запись f( )= .
Рассм.
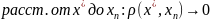 .
.
Рассм.
f(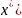 )≤
)≤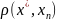 +
(
.
f(
+
(
.
f(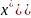 =
+
f(
),
f(
=
+
f(
),
f(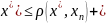 α
)→0.
α
)→0.
Т.о.
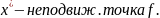
4)
Докажем, что
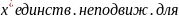 f.
f.
Предположим
противное:
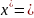 f(
)
и
f(
)
и
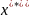 =
f(
)
(
=
f(
)
(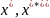 )=
(f(
),f(
))≤α
(
<
(
)=
(f(
),f(
))≤α
(
<
(
Точки
получ. по ф-ле
=f(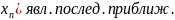 к реш.
к реш.
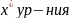 x=f(x).
x=f(x).
Итак
справедлива оценка
(
)≤
(
),
если потреб. Чтобы l→∞,
то получ. что
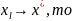 тогда
мы получ. оценку погрешн.
(
,
)≤
(
).
тогда
мы получ. оценку погрешн.
(
,
)≤
(
).
Правая часть нер-в→0 со скор. , а эта скорость→0 геометр. прогрессии. Такая скорость-линейная.
10.
Пусть надо решить F(x)=0
(1), где F(x)
– вещ. ф-ция вещ. аргумента. Запишем
ур-ние 1 в виде x=f(x)
(2). Сделаем так: умножим рав-во 1 на ф-цию
ψ(x),
где ψ(x)
– непрерывная знакопостаянная ф-ция.
Далее прибавим x.
x–
ψ(x)*F(x)=x.
Пусть к/им-то обр. нашли нач. приближение
решение
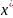 ур-ия 1, тогда остальные прибл-ия будут
наход-ся по ф-ле
ур-ия 1, тогда остальные прибл-ия будут
наход-ся по ф-ле
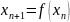 (3). Далее 3 будет наз. м-дом
простой итерации.
Т-ма
о сходности м-да:
пусть выполн. условия: 1)
f(x)-
определена и непрерывна на промежутке
(3). Далее 3 будет наз. м-дом
простой итерации.
Т-ма
о сходности м-да:
пусть выполн. условия: 1)
f(x)-
определена и непрерывна на промежутке
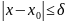 и удовлетворяет условию
Липшица:
и удовлетворяет условию
Липшица:
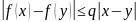 , при
, при
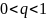 . 2)для
нач приближения
. 2)для
нач приближения
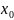 выполн.
выполн.
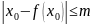 3)
числа
m,
3)
числа
m,
 ,
q
связ соотнш-ем
,
q
связ соотнш-ем
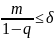 , тогда ур-ние 1 в обл
им. единственное решение
,
к к/му сходится итерац. процесс 3 со
скоростью
, тогда ур-ние 1 в обл
им. единственное решение
,
к к/му сходится итерац. процесс 3 со
скоростью
 (4). Док-во т-мы аналог-но док-ву пр-ципа
Банаха. Замечание:
условие Липшица с
для ф-ции f(x)
на
выполн-ся, если сущ-ет производная
данной ф-ции f`(x).
(4). Док-во т-мы аналог-но док-ву пр-ципа
Банаха. Замечание:
условие Липшица с
для ф-ции f(x)
на
выполн-ся, если сущ-ет производная
данной ф-ции f`(x).
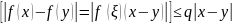 Из-за оценки 4 =>, что м-д итераций 3
сход-ся со скоростью геометр. прогрессии,
т.е. линейной. Т.к. итерац. процесс
бесконечен, то надо использ. правило
останова: 1) по невязке
Из-за оценки 4 =>, что м-д итераций 3
сход-ся со скоростью геометр. прогрессии,
т.е. линейной. Т.к. итерац. процесс
бесконечен, то надо использ. правило
останова: 1) по невязке
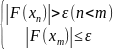 , где
, где
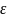 - ур-нь останова, m
– момент останова. 2) по соседним
приближениям
- ур-нь останова, m
– момент останова. 2) по соседним
приближениям
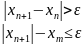 . Т.о. приближенное нахождение вещ-ых.
изолир-ых. корней ур-ния 1 делится на 2
этапа: 1. определение корней; 2. уточнение
приближ. знач. корней с помощью итерац.
м-да с заданной точностью.
. Т.о. приближенное нахождение вещ-ых.
изолир-ых. корней ур-ния 1 делится на 2
этапа: 1. определение корней; 2. уточнение
приближ. знач. корней с помощью итерац.
м-да с заданной точностью.
Пример: Методом итераций найти отрицательный корень уравнения х4 + х-3 = 0.
Решение: Данное уравнение имеет два действительных корня; отрицательный корень находится на отрезке [-1,5; -1,4], так как для его концов выполняется условие f(-1,5) * f(1,4) < 0.
Уравнение запишем в виде х = х + с(х4 + х - 3 = о), где с - постоянная. Выберем значение постоянной так, чтобы для функции
ψ(х)=х
+ с(х4 + х-3) выполнялось условие
 .
.
В качестве такого значения можно взять с = 0,1; тогда ψ(x) = 0,lx4 + l,lx-0,3,
ψ'(х)
= 0,4х3 +1,1;
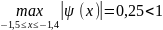 ;
;
Взяв
=
1,45, вычислим последующие приближения
по формуле
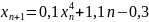 ,
где 𝛏=-1,45262
– корень ур-ия.
,
где 𝛏=-1,45262
– корень ур-ия.
Обусловленность СЛУ:
Рассм
как погрешность м-цы у столбцов free
членов влияет на реш-е сис-ы Ax=b
(1). Пусть
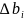 изменение i-ой
компаненты столбца b.
изменение i-ой
компаненты столбца b.
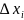 изменение
изменение
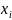 вектора;
вектора;
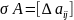 – изменение м-цы. В кач-ве меры отклонения
решения x
от x+
– изменение м-цы. В кач-ве меры отклонения
решения x
от x+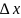 будем рассм отклонение
будем рассм отклонение
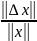 и
и
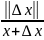 .
Если нам вместо точности правой части
известно приближ
.
Если нам вместо точности правой части
известно приближ
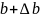 тогда вместо сис-ы 1 решаем си-у Ax=
и мерой отклонения
к
будет число, т.е. оцениваем
тогда вместо сис-ы 1 решаем си-у Ax=
и мерой отклонения
к
будет число, т.е. оцениваем
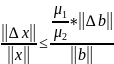 ,
где
,
где
 –найбольш
сингулярное число м-цы А,
–найбольш
сингулярное число м-цы А,
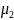 –
наимен. Примечание: сингулярные чмсла
м-цы А удовлет ур-ию
–
наимен. Примечание: сингулярные чмсла
м-цы А удовлет ур-ию
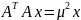 .
В случ если А симметрич, т.е.
.
В случ если А симметрич, т.е.
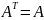 тогда сингул числа будут = модулям
собственных значений. Число
тогда сингул числа будут = модулям
собственных значений. Число
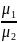 число обусловленности для невырожд
м-цы А. Вместо м-цы 1 б. решать сис-у
(А+
число обусловленности для невырожд
м-цы А. Вместо м-цы 1 б. решать сис-у
(А+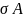 )
=
)
=
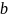 мера отклонения в этом случае
мера отклонения в этом случае
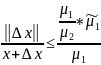 ,
где
,
где
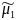 –
наибольш сингуляр число м-цы А. Если
относит-но мало то м-ца А хорошо
обусловлена по отнош к решению сис-ы
1, иначе плохо обусловлена.
–
наибольш сингуляр число м-цы А. Если
относит-но мало то м-ца А хорошо
обусловлена по отнош к решению сис-ы
1, иначе плохо обусловлена.
11.
Пусть на нек/ом [a,b]
ф-ция F(x)
и F`(x)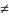 0
и F``(x)
0,
F(a)F(b)<0
на концах отрезков ф-ция меняет знак
из условия следует ур-ние F(x)=0
имеет только один корень. Запишем ур-ие
1 в виде x=f(x)
– 2. Домножим на ψ(x)
непрерывную в окрестности точки
.
В кач-ве ψ(x)
возьмем конкретную ф-цию
0
и F``(x)
0,
F(a)F(b)<0
на концах отрезков ф-ция меняет знак
из условия следует ур-ние F(x)=0
имеет только один корень. Запишем ур-ие
1 в виде x=f(x)
– 2. Домножим на ψ(x)
непрерывную в окрестности точки
.
В кач-ве ψ(x)
возьмем конкретную ф-цию
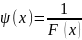 . Отсюдо получим
. Отсюдо получим
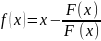 .
Пусть к/им-то обр. будет выбрано
– нач. приближение решения
ур-ия 1. Тогда остальные приближения
рассчит-ся по ф-ле:
.
Пусть к/им-то обр. будет выбрано
– нач. приближение решения
ур-ия 1. Тогда остальные приближения
рассчит-ся по ф-ле:
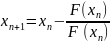 (3) метод
Ньютона.
Необход док-ть:
(3) метод
Ньютона.
Необход док-ть:
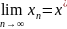 .
Для док-ва сходимости 3 нам надо док-ть,
что f-
сжатие.
.
Для док-ва сходимости 3 нам надо док-ть,
что f-
сжатие.
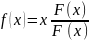 .
.
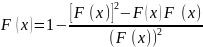 Пусть x=
Пусть x=
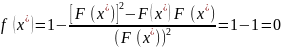 .
f(x)–непрерывна
на [a,b],
а из непрерывности f
`(x)
следует, что сущ-ет окрестность точки
,
т/ая что
.
f(x)–непрерывна
на [a,b],
а из непрерывности f
`(x)
следует, что сущ-ет окрестность точки
,
т/ая что
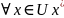 .
.
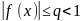 .
Отсюда следует главный вывод: если
.
Отсюда следует главный вывод: если
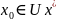 и кроме этого
и кроме этого
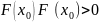 ,
то отображение f(x)
явл. Сжатием и по пр-ципу Банаха м-д 3
будет сход-ся к
.
Получим скорость сходимости м-да 3. Для
этого разложим ф-цию F(x)
в ряд Тейлора в опр. точке
,
то отображение f(x)
явл. Сжатием и по пр-ципу Банаха м-д 3
будет сход-ся к
.
Получим скорость сходимости м-да 3. Для
этого разложим ф-цию F(x)
в ряд Тейлора в опр. точке
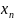 .
.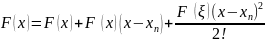 ,
𝛏
,
𝛏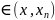 .
.
x=
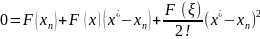 ,
т.к. производная ф-ции
0,
то
,
т.к. производная ф-ции
0,
то
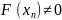 ,
тогда
,
тогда
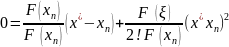 (4). В ф-ле 3 вычислим
:
(4). В ф-ле 3 вычислим
:
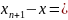
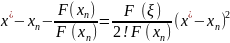 . Если обознач. в кач-ве
. Если обознач. в кач-ве
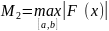 и
и
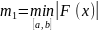 , тогда
, тогда
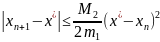 (5). Замечание:
если удаётся получить нер-во
(5). Замечание:
если удаётся получить нер-во
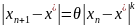 , где
, где
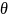 – символ Ландао. Если k
= 1, то сходимость м-да линейная; k
= 2, то квадратичная; k
= 3, то кубическая; k
> 1, то сверхлинейная. Тогда из 5 следует
что скорость сходимости м-да квадратичная.
Получим оценку погрешности для м-да 3.
Для этого потребуем, чтобы нач приближение
выбиралось из усл.:
– символ Ландао. Если k
= 1, то сходимость м-да линейная; k
= 2, то квадратичная; k
= 3, то кубическая; k
> 1, то сверхлинейная. Тогда из 5 следует
что скорость сходимости м-да квадратичная.
Получим оценку погрешности для м-да 3.
Для этого потребуем, чтобы нач приближение
выбиралось из усл.:
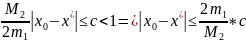 ;
;
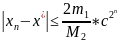 –
оценка
погрешности м-да (оценка скорости
сходимости). При переходе от 1 итерац.
К др. в м-де Ньютона число верных знаков
в последних приближениях
–
оценка
погрешности м-да (оценка скорости
сходимости). При переходе от 1 итерац.
К др. в м-де Ньютона число верных знаков
в последних приближениях
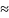 удваиваются. Достоинства:
высокая скорость сходимости; Недостатки:
узкая область сходимости.
удваиваются. Достоинства:
высокая скорость сходимости; Недостатки:
узкая область сходимости.
Геометрический смысл м-да Ньютона
F(x) = 0 на [a, b] F(a) F(b)=0
Проведем
ч/з т. a
касательную y=F
`(a)+
F
`(a)(x-a)
и найдем ее пересечение 0=F(a)+F`(a)(x-a);
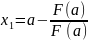 при F
`(a)
0.
Ч/з точку
при F
`(a)
0.
Ч/з точку
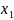 проведем новую касательную y=F
`(
)+
F
`(
)(x-
).
При у=0
проведем новую касательную y=F
`(
)+
F
`(
)(x-
).
При у=0
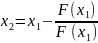 .
Т.о. м-д Ньютона – это м-д касательных.
.
Т.о. м-д Ньютона – это м-д касательных.
12. Будем решать ур-ие: F(x)=0 (1), где F(x) – дважды дифф-ая непрерывная ф-ция на [a, b]. F`(x) 0 и F``(x) 0 на [a, b], F(a)F(b)<0. Приведем ур-ие 1 к виду: x=f(x) (2).
–ψ(x)F(x)=0
 –ψ(x)F(x)+x=x
x–
ψ(x)F(x)=x
(x–
ψ(x)F(x)=f(x)).
Пусть ψ(x)=
–ψ(x)F(x)+x=x
x–
ψ(x)F(x)=x
(x–
ψ(x)F(x)=f(x)).
Пусть ψ(x)=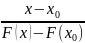 .
Т.о. получим, что
.
Т.о. получим, что
 .
Будем считать, что ф-ция ψ(x)
непрерывна в окрестности т.
и надо, чтобы выполнялось F(
)*
F``(
)
.
Т.о., получим новый итерац. м-д:
.
Будем считать, что ф-ция ψ(x)
непрерывна в окрестности т.
и надо, чтобы выполнялось F(
)*
F``(
)
.
Т.о., получим новый итерац. м-д:
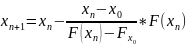 (3) метод
хорд.
Покажем, что итерац. процесс 3 сходится
к ур-ию 1, т.е. убедимся, что f(x)–сжатие.
(3) метод
хорд.
Покажем, что итерац. процесс 3 сходится
к ур-ию 1, т.е. убедимся, что f(x)–сжатие.
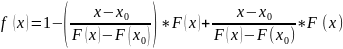 ;
; (+). Разложим ф-цию F(x)
в ряд Тейлора в т.
:
(+). Разложим ф-цию F(x)
в ряд Тейлора в т.
:
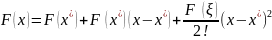 ,
𝛏
(x,
).
Подставим в последнее рав-во вместо x
получим:
,
𝛏
(x,
).
Подставим в последнее рав-во вместо x
получим:
 (*). При n=0:
(*). При n=0:
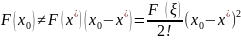 ;
;
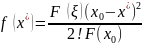 ;
;
;
;
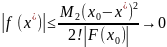 при
при
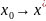 .
Т.о.
.
Т.о.
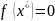 ,
тогда из непрерывности ф-ции f`(x)
=>
,
тогда из непрерывности ф-ции f`(x)
=>
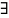 окрестность U(
)
такая, что
окрестность U(
)
такая, что
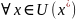 будет выполняться
.
Если взять нач. приближение из U(
),
то тогда будет выполняться условие
Липшица и м-д 3 будет сход-ся.
будет выполняться
.
Если взять нач. приближение из U(
),
то тогда будет выполняться условие
Липшица и м-д 3 будет сход-ся.
Получим
оценку погрешности м-да 3:
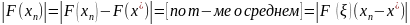 ,
𝛏
(
,
𝛏
(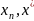 ).
Выразим
).
Выразим
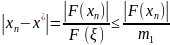 ,
где
,
где
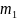 –
–
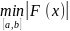 .
.
Скорость
сходимости м-да 3 – линейная .
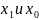 выбираются так, что
выбираются так, что
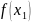 и
и
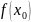 были разного знака. Достоинства:
широкая обл. сходимости; недостатки:
небольшая скорость.
были разного знака. Достоинства:
широкая обл. сходимости; недостатки:
небольшая скорость.
Частные случаи
;
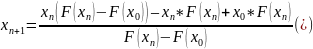
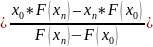 .
.
Пусть
в **
= b:
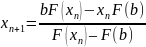 .
.
По
последней ф–ле считают, что если
известно F(b)*
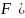 )
>o
,
=0.
)
>o
,
=0.
Пусть
в **
= а:
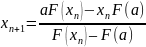 .
.
Если F(а)* ) >o, =b. График 1.
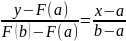 .
Преобразовав это ур-ие с учетом
пересечения OX.
(AB)
.
Преобразовав это ур-ие с учетом
пересечения OX.
(AB)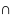 OX
=>y=0
OX
=>y=0
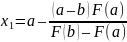
Если )> , то f(x) вогнутая ф-ция; если )<0, то f(x) выпуклая ф-ция.
Графики (4).
Метод
хорд им. Линейную скорость сходимости
и оценку погрешности
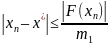 .
.
Если
в ф-ле 3 вместо
взять
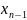
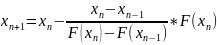 (4),
то ф-ла 4 наз-ся методом секущих. Для
м-да секущих в ф-ле
(4),
то ф-ла 4 наз-ся методом секущих. Для
м-да секущих в ф-ле
,
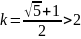 =>скорость сверхлинейная.
=>скорость сверхлинейная.
