
- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
Бол-во физ. задач решаются при помощи мат. Знаков один из методов решения таких задач-это эксперимент.Второй-матем. исследование физ. явления.Такое исслдед. применяется не к реал. Физ. процессу, а к его мат. модели.первая стадия при решении задачи – это постановка задачи или формул- мат. модели.2-ая задача – матем. Модели в завис. От её применения.Числ. методы делятся на:
- точные(дают решение задачи через конечное число арифм. Действий причём, если
исх. данные известны точно и вычисл. производ. без округл., то и вычисл. произв. точно-м. Гауса,Крамера и процесс ортогонализации)
- приближённые или итерационные методы (дают бескон. послед. приближенный, предел кот. если он Э явл. решением задачи – метод простой итерации, метод касат. реш.ур-ний и сист. ур-ний метод секущих, метод Зейделя.
При решении мат. задач важно знать корректно ли решаемая задача. Большинство некорректных задач записано в виде операторного уравнения 1-го рода.
Ax=y
(1), x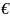 X,
y€Y.
A:x→Y,
где А не обяз. лин. оператор.
X,
y€Y.
A:x→Y,
где А не обяз. лин. оператор.
Опр: задача отыскания решения х ур-ния 1 наз. корректной по Адамару, если при любой фиксированной части у0, если ее решение:
1)существует в Х
2)единственное в Х
3)устойчивое в Х
Если, хотя бы одно из условий нарушается, то задача наз. некорректной, большинство физ. задач некорректны.
Мн-во
х произв.эл-ов наз. метрическим пр-вом,
если любым эл-ам х,у став. в соотв.
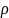 (х,у)
наз.расст.между х,у (метрикой)
удовл.след.условиям:
(х,у)
наз.расст.между х,у (метрикой)
удовл.след.условиям:
1)
(х,у) 0
и
(х,у)=0
если х=у
0
и
(х,у)=0
если х=у
2) (х,у)= (у,х)
3) (х,z)
Послед.
{хn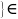 х
наз.сходящейся если к х*
х
наз.сходящейся если к х* х если метрика между
{хn,xm}
х если метрика между
{хn,xm}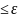 .
.
Послед. {хn х наз. фундаментальной или сход. в себе, если для любого ε>0 существует N, что для любых n, m>N {хn,xm} .
Метр.пр-во в коп. всякая фунд.послед.сходится наз.полным.
Пусть
х,у-метр.пр-ва,отображение f:х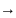 Y
наз.оператором заданное в х со знач.у,то
f-отображ.метрич.пр-во
на себя.Если f(х)=х,где
х
х,то
х-неподвиж.точка отображ. f.
Y
наз.оператором заданное в х со знач.у,то
f-отображ.метрич.пр-во
на себя.Если f(х)=х,где
х
х,то
х-неподвиж.точка отображ. f.
Говорят,
что отображение f:x→X
наз. сжимающим, если для любых элементов
х,у
Х существует q<1
(f(x),
f(y))≤q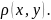
Метод оптимального исключения по существу является вариацией метода Гаусса. Идея этого метода состоит в том, что последовательным исключением неизвестных матрица системы приводится к диагональному виду. Возможность же таких эквивалентных преобразований следует из теоремы о приведении матрицы к диагональному виду.
Теорема.
Для
любой квадратной вещественной матрицы
А
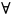 порядка существуют такие квадратные
вещественные матрицы и
и
v
(п-го
порядка), что матрица UAV
-
диагональная. (см. с. 29).
порядка существуют такие квадратные
вещественные матрицы и
и
v
(п-го
порядка), что матрица UAV
-
диагональная. (см. с. 29).
