
- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
Метод
пр-ов основан на опр-ии самого интеграла
и егогеометрического значения. Пусть
 ,
,

Формула
левых пр-ов:

Формула
правых пр-ов:

Абсолютная
погрешность МЛП и МПП:
 .
Погрешность –
.
Погрешность –

Формула
средних пр-ов:
 огрешность
–
огрешность
–

Правило
Рунге на примере формулы Симпсона.
Пусть
 -приближенное
значениеинтеграла, вычесленное шагом
h.
-приближенное
значениеинтеграла, вычесленное шагом
h.
Уменишение
на шаг h
в 2 раза, разбив отрезок [a,b]
на [a,c]
и [c,b],
т.е.
 .
.
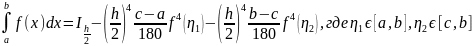
Предположим,
что ф-ция
 меняется
не слишком быстро, т.е.
меняется
не слишком быстро, т.е.
 .
Тогда
.
Тогда
 и
и

Следовательно,
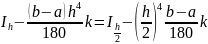
 .
.
Вывод:

 требуемая
точность. Тогда шаг h
подходит для вычисления интегралов с
достаточной точностью. Если получилось,
что
требуемая
точность. Тогда шаг h
подходит для вычисления интегралов с
достаточной точностью. Если получилось,
что
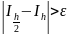 ,
то расчет повторяют шагом
,
то расчет повторяют шагом
 и затем сравнивают значения интегралов
и затем сравнивают значения интегралов
 – это правило Рунге.
– это правило Рунге.
28.
В курсе ДУ узуч-ся м-ды реш-ия простейших
видов этих ур-ий. Ду, к/ые м. реш. т\ми
м-дами встреч редко ⟹приобретает важное
знач-е приближенное реш-ие ДУ. Их 2
класса: аналит
(дают реш-е
в виде аналит выражения)
и численные
(в виде таблицы численных значений)
м-ды.
Пусть
надо решить ДУ на [ ].
].
 задача
Коши и пусть выполняются условия: 1)
ф-ция
задача
Коши и пусть выполняются условия: 1)
ф-ция
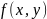 сколь угодно раз дифф-ма по x,y
(облад нужной жадностью); 2) ф-ция y(x)
им нужное число производных тогда м.
применить м-д степенных рядов решения
ДУ.
сколь угодно раз дифф-ма по x,y
(облад нужной жадностью); 2) ф-ция y(x)
им нужное число производных тогда м.
применить м-д степенных рядов решения
ДУ.
М-д
степенных рядов:
разложим y(x)
в ряд Тейлора в т.
:
y(x)=y(
)+ где h=x-
,
где h=x-
,
 ,
,
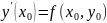 .
.
 Вкач-ве приближ знач ДУ возьмем ф-цию
Вкач-ве приближ знач ДУ возьмем ф-цию
 получ путем подстановки
получ путем подстановки
 в ряд Тейлора. Замеч:
для знач x
близких к
м-д степенных рядов для достаточно
больших m
дает достаточно хорошее приближ к
точному реш-ю y(x)
к задаче *. Но если величина
в ряд Тейлора. Замеч:
для знач x
близких к
м-д степенных рядов для достаточно
больших m
дает достаточно хорошее приближ к
точному реш-ю y(x)
к задаче *. Но если величина
 велика, то величина
велика, то величина
 тоже
большая. М-д степ рядов становиться
непригодным, когда
x
выходит
из обл. сходимости ряда Тейлора.
тоже
большая. М-д степ рядов становиться
непригодным, когда
x
выходит
из обл. сходимости ряда Тейлора.
М-д
Пикара:
позволяет получать в аналит виде послед
приближений. ,
,
 . Этот м-д редко исп., т.к. есть недостаток:
каждый шаг требует вычислений интеграла.
. Этот м-д редко исп., т.к. есть недостаток:
каждый шаг требует вычислений интеграла.
М-д
Эйлера:
будем реш задачу Коши для ДУ 1-го порядка.
 .
Заменим 1 и 2 на
.
Заменим 1 и 2 на
 .
.
Предположим, что ф-ция f(x) непрер по переем на отрезке на замкнут обл Д.
Относ
 для ф-ции
для ф-ции
 выполн усл Липшица
выполн усл Липшица

М-д
Эйлера сост в замене производной
разностью отношений
 тогда
на отр [
тогда
на отр [ ]:
]:
 .
.
 .
Пусть
.
Пусть
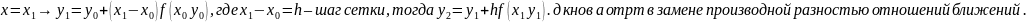 Т.о. обыкновенный м-д Эйлера им. вид:
Т.о. обыкновенный м-д Эйлера им. вид: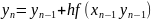 ,
где
,
где
 Выч-ие знач по м-ду Эйлера дает менее
грубое приближение к задаче Коши.
Поэтому м-д Эйлера исп-ся тогда, когда
надо приближ представление о решении
на небольшом отрезке. Если ф-ция f(x,y)
из 1 непрерывна по x
на отрезке (a,b)
из обл. Д
и удовлет. усл. Липшица по y.
Если известно
Выч-ие знач по м-ду Эйлера дает менее
грубое приближение к задаче Коши.
Поэтому м-д Эйлера исп-ся тогда, когда
надо приближ представление о решении
на небольшом отрезке. Если ф-ция f(x,y)
из 1 непрерывна по x
на отрезке (a,b)
из обл. Д
и удовлет. усл. Липшица по y.
Если известно
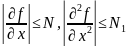 ,
то м. записать оценку погрешн.:
,
то м. записать оценку погрешн.:
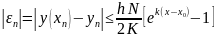 .
.
Рассмотр его модификации:
Модиф-ый
м-д Эйлера:
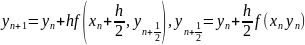 ;
М-д
Эйлера – Коши:
;
М-д
Эйлера – Коши:
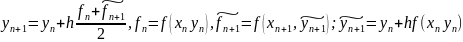 ;
;
«+»: прпостота; малый объем вычислений; наглядность. «–»: малая точность; работает для небольших интервалов.
Более
точным м-дом реш-я ДУ 1 порядка – м-д
Рунге–Кутта:
 ;
;
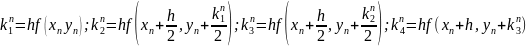
М-д Р-К облад повыш точностью, но работа по нему очень трудоемкая. «–»: нет действенного контроля. Обычно контроль осущ-ся так: сначала проводят счет с шагом h, 2h и получ рез-ты сравнивают. Если при этом модуль разности не превосходит заданной величины погреш-ти то счет продолж с шагом h, иначе шаг уменьш вдвое.
29.
Стандарт ЗЛП состоит в: найти наибольш
неотриц решение сис-ы
 (m–линейных
нер-в с n–переменными),
при к/ом линейная форма f=cx
принимает max(min)
знач. Всякое неотриц реш-е сис-ы наз
допустимым. Оно наз оптимальным, если
она максимиз-ет (минимиз-ет) линейную
форму
f=cx.
(m–линейных
нер-в с n–переменными),
при к/ом линейная форма f=cx
принимает max(min)
знач. Всякое неотриц реш-е сис-ы наз
допустимым. Оно наз оптимальным, если
она максимиз-ет (минимиз-ет) линейную
форму
f=cx.
Сис-а
вида
наз сис-ой
ограничений
для ЗЛП. Если в кач-ве этой сис-ы выступает
СЛУ то ЗЛП наз канонической.
От стандарт ЗЛП м. перейти к канонической.
Запишем
в виде:
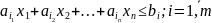 и добавим к кажд. т/ой строке
и добавим к кажд. т/ой строке
 так чтобы получ:
так чтобы получ:
 .
Тогда вместо
получ Ax+Ez=b,
где Z=(
.
Тогда вместо
получ Ax+Ez=b,
где Z=( ).
Последняя запись уже СЛУ, т.е. получ
канонич
ЗЛП.
).
Последняя запись уже СЛУ, т.е. получ
канонич
ЗЛП.
М.
осуществить обратный переход: Ax=b.
 ,
а это стандарт. ЗЛП.
,
а это стандарт. ЗЛП.
Примеры
ЗЛП: транспорт. задача: m–число
складов; n–число
магазинов;
 –число
ед-ц товара, выделенных i-ым
кладовщиком;
–число
ед-ц товара, выделенных i-ым
кладовщиком;
 –число
ед-ц товара, необход j-му
магазину;
–число
ед-ц товара, необход j-му
магазину;
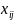 –число
ед-ц товара перевоз с i-го
склада в j-ый
магазин;
–число
ед-ц товара перевоз с i-го
склада в j-ый
магазин;
 –стоимость
перевозки одной ед-цы товара с i-го
склада в j-ый
магазин. Найти min
линейной формулы (транспортной издержки)
–стоимость
перевозки одной ед-цы товара с i-го
склада в j-ый
магазин. Найти min
линейной формулы (транспортной издержки)
 при след–их огранич:
при след–их огранич:
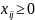 ,
i=
;
j=
,
i=
;
j=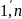 .
.
 ;
;
 .
.
Задача
планир–ия произ–ва: m–число
ресурсов; n–число
товаров;
 –число
ед-ц i-го
ресурса, необход для пр-ва ед-цы j-го
товара;
–число
ед-ц i-го
ресурса;
–число
ед-ц i-го
ресурса, необход для пр-ва ед-цы j-го
товара;
–число
ед-ц i-го
ресурса;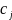 –
доходы от ед-цы j-го
товара;
–
доходы от ед-цы j-го
товара; –
запланир ур-нь пр-ва j-го
товара. Найти max
линейной формулы
–
запланир ур-нь пр-ва j-го
товара. Найти max
линейной формулы
 при ограничениях:
при ограничениях:

