15Понятие корня

Алгебраические выражения, содержащие операцию извлечения корня, называются иррациональными.

Корнем n-й степени из числа a называется такое число b, n-я степень которого равна a (n ≥ 2). Обозначается  , где a - подкоренное выражение (или число), n - показатель корня (n ≥ 2; n ϵ N).

По определению  , если bⁿ = a, или  .

Основные свойства корня

Если корни рассматривать в множестве действительных чисел, то:      а) корень четной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку;      б) корень четной степени из отрицательного числа в множестве действительных чисел не существует;      в) корень нечетной степени из положительного числа имеет только одно действительное значение, которое положительно;      г) корень нечетной степени из отрицательного числа имеет только одно действительное значение, которое отрицательно;      д) корень любой натуральной степени из нуля равен нулю.

Действие, посредством которого отыскивается корень n-й степени из данного числа a, называется извлечением корня n-й степени из числа a, а результат извлечения корня в виде   называют радикалом.

Таким образом, множество действительных чисел не замкнуто относительно извлечения корня четной степени, а результат этого действия (корень) не однозначен.

Заметим, что множество действительных чисел замкнуто относительно извлечения корня нечетной степени, а результат этого действия однозначен.

Арифметический корень и его свойства

Арифметическим значением корня или арифметическим корнем степени n (n ≥ 2; n ϵ N) из положительного числа a называется положительное значение корня. Корень из нуля, равный нулю, также будет называться арифметическим корнем, т. е.   есть арифметический корень, где a ≥ 0,b ≥ 0 и bⁿ = a.

Множество неотрицательных действительных чисел замкнуто относительно извлечения арифметического корня, а результат этого действия однозначен. Это значит, что для любого неотрицательного числа a и натурального числа n (n > 1) всегда найдется, и притом только одно, такое неотрицательное число b, что bⁿ = a.

16Свойства степени с рациональным показателем.

Определение. Степенью числа a>0 с рациональным показателем  ,  где m - целое число, а n - натуральное ( n>1), называется число  , т.е.

Свойства степени с рациональным показателем.

Рекомендации к теме теория >>

При упрощении выражений, содержащих корни и степени с дробным показателем, можно переходить только к корням или только к степеням. Вы можете сами выбрать наиболее удобный для Вас путь решения задачи, мы Вам рекомендуем чаще пользоваться преобразованием выражений с помощью степени с дробным показателем и ее свойств. Свойства степеней имеют более простую форму и уменьшают вероятность совершения ошибки при преобразовании.

При выполнении упражнений на вычисление, упрощение выражений, содержащих степени с рациональным показателем, используют определение и свойства степени.

17-18ЛОГАРИФМ, число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление – вычитанием, возведение в степень – умножением и извлечение корней – делением.

Общее описание. Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (10² = 100). Если n – заданное число, b – основание и l – логарифм, то b^l = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений log_b n = l и antilog_b l = n.

Основные свойства логарифмов:

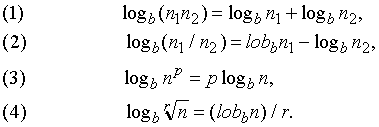
Логарифмическая функция. Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы – в геометрической, представлен на рис. 2,а. График обратной, или показательной (экспоненциальной), функции y = e^x, ординаты которого возрастают в геометрической прогрессии, а абсциссы – в арифметической, представлен, соответственно, на рис. 2,б. (Кривые y = logx и y = 10^x по форме аналогичны кривым y = lnx и y =e^x.) Были предложены также альтернативные определения логарифмической функции, например,

Основное логарифмическое тождество
Покажем как можно любую функцию вида abсделать экспоненциальной. Поскольку функция вида ех называется экспоненциальной, то
Любая функция вида a bможет быть представлена в виде степени десяти

19 Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси.  Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

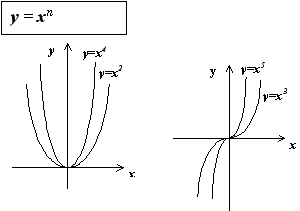
К основным свойствам степенной функции y = x ^a при a > 0 относятся:

• Область определения функции - промежуток (0; +  ).

• Область значений функции - промежуток (0; + ).

• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если x₁ <x₂ то a^r₁ < a^r₂ .

• График степенной функции при a > 0 изображен на рисунке.

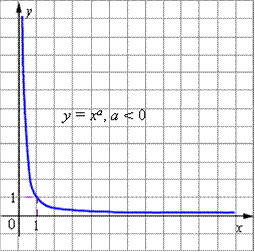
К основным свойствам степенной функции y = x ^a при a < 0 относятся:

• Область определения функции - промежуток (0; + ).

• Область значений функции - промежуток (0; + ).

• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если x₁ <x₂ то a^r₁ > a^r₂ .

• График степенной функции при a < 0 изображен на рисунке.

Справедливы следующие свойства степенной функции: 

• x^a₁x^a₂ = x^a₁ ^{+ a}₂

• x^a₁ : x^a₂ = x^a₁ ^{- a}₂

• (x^a₁)^a₂ = x^a₁ ^a₂

• x^a₁ > x^a₂, x > 1, a₁ > a₂

• x^a₁ < x^a₂, 0 < x < 1, a₁ < a₂

• Степенна́я фу́нкция — функция 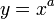 , где   (показатель степени) — некоторое вещественное число^[1]. К степенным часто относят и функцию вида 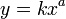 , где k — некоторый масштабный множитель.^[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом.

20Показательная функция — математическая функция  , где   называется «основанием», а   — «показателем» степени.

• В вещественном случае основание степени   — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.

• В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.

• В самом общем виде — 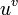 , введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

При a > 0, a  = 1, определена функция y = a ^x , отличная от постоянной. Эта функция называетсяпоказательной функцией с основанием a. 

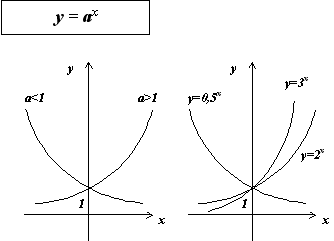
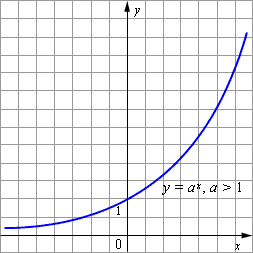
Основные свойства показательной функции y = a ^x при a > 1:

• Область определения функции - вся числовая прямая.

• Область значений функции - промежуток (0;+ ).

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x₁< x_{2 ,} то a^x₁< a^x₂ .

• При x = 0 значение функции равно 1.

• Если x > 0 , то a ^x > 1 и если x < 0, то 0 < a < 1.

Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.

Основные свойства показательной функции y = a ^x при 0 < a < 1:

• Область определения функции - вся числовая прямая.

• Область значений функции - промежуток (0;+ ).

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x₁< x_{2 ,} то a^x₁> a^x₂ .

• При x = 0 значение функции равно 1.

• Если x > 0 , то 0 < a < 1 и если x < 0, то a ^x > 1.

К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:

• a^x₁ a^x₂ = a^x₁^+ x₂, для всех x₁ и x_2.

• a−x=(ax)−1=1ax для любого x.

• nax=axn  для любого x и любого n N n =1 .

• (ab)^x = a^x b^x для любых a, b > 0; a,b =1 .

• (ba)x=bxax  для любых a, b > 0; a,b =1 .

• a^x₁ = a^x₂, то x₁ = x_2.