
ИСМ
.docx1. Модель. Моделирование. Виды моделирования. Преимущества математического моделирования Модель — объект (физический или абстрактный) максимально приближенный к исследуемому объекту, системе, явлению и т.д. с точки зрения решаемой задачи. Моделирование — процесс создания, отладки и использования модели. Моделирование: 1) Физическое, 2) Математическое: аналитическое, компьютерное(численное, имитационное, статистическое) Физическое моделирование предполагает, что в качестве модели используется либо сама исследуемая система, либо другая система с той же или подобной физической природой. Математическая модель M предполагает установление соответствия данной реальной системе S некоторой совокупности математических методов, описывающих исходную систему с достаточной, для поставленной задачи, точностью. Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых математических соотношений (алгебраических, интегро-дифференциальных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным методом; в) качественным, когда не имея решений в явном виде, можно найти некоторые свойства решения. Компьютерное моделирование подразумевает создание моделирующей программы для ЭВМ, позволяющей проводить с ней вычислительные эксперименты. |
2. Понятие сложной системы. Ее составляющие Элементом m назовем некоторый объект (материальный, энергетический, информационный), обладающий рядом свойств, обеспечивающих выполнение некоторых функций, внутреннее строение (содержание) которого для целей исследования не представляет интереса. Связью l между элементами назовем процесс их взаимодействия, важный для целей исследования. Системой C наз. совокупность элементов со связями и целью функционирования, отличной от целей функционирования составляющих его элементов. Сложной системой S наз. система, состоящая из разнотипных элементов с разнотипными связями. Формально под сложной системой S будем понимать тройку множеств: S = {{m}, {l}, F}, где {m} — множество априорно выделенных элементов системы; {l} — комплекс как взаимных связей между элементами, так и связей между элементами и внешней средой; F — функция, описывающая цель функционирования системы. Большой системой G называется система, состоящая из большого числа однотипных элементов с однотипными связями. Отличия между большой и сложной системой достаточно условны, также как различия между элементом и системой. Структурой системы называется ее расчленение (декомпозиция) на группы элементов с указанием связей между ними. Для любой сложной системы характерно функционирование во времени, поэтому целесообразно определить ее динамические характеристики.
|
3. Непрерывно-детерминированные модели. В этих моделях время t ∈ [t0, T] полагается непрерывной переменной, а случайными факторами в системе S пренебрегают. Основной математический аппарат, используемый при исследовании НД-моделей, это теория интегральных и дифференциальных уравнений. Разберем особенности НД-моделирования на примере использования дифференциальных уравнений. Пример 1. Пусть подлежащей моделированию системой S является электрический колебательный контур с двумя параметрами: емкостью С и индуктивностью L. Состояние этой системы в момент t будем характеризовать величиной заряда конденсатора Q(t). Из физики известно, что математическая модель будет иметь вид:
где
V(t)
— внешнее детерминированное
электрическое воздействие на контур.
Если V(t)
≡ 0, и можно представить Q(0)
= A
cosϕ,
то решение однородного уравнения
имеет вид:
|
4.Дискретно-детерминированные модели (ДДМ). В ДДМ время t является дискретной переменной: t = τ ⋅ ∆, где ∆ — шаг дискретизации; τ = 0, 1, 2,… — «дискретное время». Основной математический аппарат, используемый при построении ДД-моделей, это теория разностных уравнений и аппарат дискретной математики, в частности — теория конечных автоматов. Разностное ур-ие — это уравнение, содержащее конечные разности искомой функции:
Другой математ. аппарат для построения ДД-моделей — теория конечных автоматов. Конечный автомат (КА) — это ММ дискретной системы S, кот под действием входных сигналов u ∈ U вырабатывает выходные сигналы y ∈ Y и которая может иметь некоторые изменяемые внутренние состояния x ∈ X, где U, Y, X — конечные множества (алфавиты). Конечный автомат характеризуется 6-ю элементами: 1. входным алфавитом U 2. выходным алфавитом Y 3. внутренним алфавитом состояний X 4. начальным состоянием x0 ∈ X 5. функцией переходов x′ = Ф(x, u); XU → Х 6. функцией выходов y = Ψ(x, u); XU → Y
|
||||||||||||||||||||||||||||||||
5.Дискретные вероятностные модели. Основной математический аппарат используемый для построения и исследования ДВ-моделей, это теория разностных стохастических ур-ий и теория вероятностных автоматов. Разностное
стохастическое ур-ие
— это такое ур-ие, кот содержит
случайные параметры θ и/или случайные
входныевоздействия { В качестве примера можно рассмотреть колебательный контур в кот случайными явл его основные пар-ры емкость конденсатора C и индуктивность катушки L. (что может иметь место т.к. эти пар-ры могут меняться со временем, например под действием изменения температуры). Случайным может быть и V(t) — внешнее электрическое воздействие на контур. Вероятностный автомат — есть конечный автомат, в кот ф-ция переходов x′ = Ф(x, u) и/или функция выхода y = Ψ(x, u) являются случайными функциями, имеющими некоторые вероятностные распределения. Введем обозначения:
Матем. модель вероятностного автомата полностью определ. 5 элементами U, Y, X, P, π.
|
6.Непрерывно-вероятностные модели . При построении и исследовании НВ-моделей используется теория стохастических дифференциальных ур-ий и теория массового обслуживания. Стохастическое
дифференциальное уравнение
в форме Ито имеет вид
коэффициенты b(⋅) и а(⋅) решение этого стохастического дифференциального ур-ия является марковским диффузионным процессом. Такая НВ-модель используется для моделирования стохастических систем управления, процессов тепло- и массообмена. Теория массового обслуживания (ТМО) применяется для построения математ. моделей таких сложных систем, для которых характерно: 1) наличие потока многих заявок на выполнение определенных операций (заявок на обслуживание); 2) наличие ногократно повторяемых операций (выходной поток). ТМО разрабатывает и исследует ММ различных по своей природе процессов функционирования экономических, производственных, технических и других систем (поставки сырья или задач для ЭВМ). При этом для таких систем характерна стохастичность: случайность моментов появления заявок, случайное время обслуживания заявки и т.д. Сложная
система являющаяся системой
массового обслуживания (СМО)
состоит из L ≥ 1 взаимосвязанных и
взаимодействующих приборов (элементов
обслуживания)
|
7. Агрегативные модели. Математическое описание процесса функционирования агрегата В тех случаях, когда аналитическая модель исследуемой системы является слишком сложной или частично либо полностью неопределена, единственным методом исследования сложных систем является имитационное моделирование. При построении агрегативной модели сложная система разбивается на конечное число взаимосвязанных элементов (подсистем). Если некоторые из полученных подсистем оказываются в свою очередь недостаточно простыми, то процесс их разделения продолжается до тех пор, пока не будут выделены элементы, допускающие стандартное математическое описание, называемое агрегатом. Под агрегатом понимают некоторое абстрактное математическое описание моделей различного типа (детерминированных, вероятностных, непрерывных, дискретных). Предположим, что за конечный интервал времени на агрегат А поступает конечное число воздействий внешней среды, управляющих сигналов и выдается конечное число выходных сигналов. При этом происходит изменение состояния агрегата. Множество всех возможных состояний агрегата будем разделять на подмножества особых состояний (ОС) и неособых состояний. Принято
говорить, что А в момент времени
|
8.Имитационное моделирование. Его виды, условия применимости, достоинства и недостатки. Всё множество математических моделей можно разделить на три подмножества: аналитические, имитационные и комбинированные. Имитационной моделью (ИМ) сложной системы СС S называются машинные программы (или алгоритмы), позволяющие имитировать на ЭВМ поведение отдельных элементов системы S, и связей между ними. Эксперименты на ЭВМ с имитационной моделью называются имитационными (вычислительными) экспериментами. Отличительные особенности ИМ: 1) при создании ИМ СС законы функционирования всей системы могут быть неизвестны (достаточно знания алгоритмов, описывающих поведение отдельных элементов системы и связей между ними); 2) в имитационной модели связи между параметрами и характеристиками системы выявляются, а значения исследуемых характеристик определяются в ходе имитационного эксперимента на ЭВМ. Условия применения ИМ: 1) широкий класс систем практически любой сложности; 2) в случаях, когда в силу сложности аналит. Модели (АМ) её практическое применение невозможно. Достоинства ИМ: 1) часто единственно возможный способ исследования СС; 2) возможность исследования системы на различных уровнях ее детализации, определяемых целью исследования; 3) возможность исследования динамики взаимодействия элементов системы во времени и пространстве параметров системы; 4) возможность оценивания характеристик системы в определённые моменты времени. |
||||||||||||||||||||||||||||||||
Опишем
процесс функционирования КА S. На
такте с номером τ (τ = 0, 1, …) на вход
автомата, находящегося в состоянии
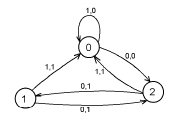
Например, булевский автомат Мили с x(0) = 0 и алфавитами U = Y = {0, 1}, X = {0, 1, 2} можно изобразить в виде графа. Вершины графа соответствуют внутренним состояниям автомата, а дуги — соответствующим переходам. Каждая дуга из x в x′ помечается парой (u, y), где u и y — входные и выходные сигналы, при кот осуществл. переход из x в x′.
|
Пример
2. Рассм.
задачу о теле брошенном под заданным
углом к горизонту:
При отсутствия трения в среде на тело будет действовать только сила притяжения, направл. вниз.
Расстояние
этой системы полностью описывается
зависимостью от времени, координат
тела и вектора скорости. Для момента
времени t
разложим
v(t)
на
vx(t)
и
vy(t),
причем
Координаты
тела в задаче описываются уравнениями:
|
Структурой системы наз ее расчленение (декомпозиция) на группы элементов с указанием связей между ними. Для любой сложной системы характерно функционирование во времени, поэтому целесообразно определить ее динамические характ-ки. Состоянием наз мн-во зафиксированных характеристик (св-тв) элементов системы, изменяющиеся при исследовании системы и важных для целей ее функционирования. Процессом (динамикой) системы наз. множество значений состояний системы, изменяющихся во времени. Целью системы наз задача получения желаемого состояния . В зависимости от способа задания закона функционирования ММ могут быть заданы аналитически, т.е. с помощью функциональных соотношений или логических условий, либо алгоритмически. Такой параметр, как время может рассматриваться как непрерывная переменная t ∈ [0, T], так и как дискретная: t = i*∆, i = 0, 1, …, M, M = [T / ∆],где ∆ — шаг дискретизации. При этом соответственно имеем непрерывные (Н) и дискретные (Д) математические модели. Если ММ не содержит случайных элементов, т.е. стохастичность системы отсутствует (или ею пренебрегаем), то имеем детерминированную модель (Д); в противном случае вероятностную (В) модель. Таким образом, по признакам непрерывности и стохастичности выделяют четыре обширных класса ММ: непрерывно-детерминированные (НД) модели; дискретно-детерминированные (ДД) модели; дискретно-вероятностные (ДВ) модели; непрерывно-вероятностные (НВ) модели. Дополнительной проблемой при моделировании сложных систем является учет одновременности функционирования элементов составляющих эту сложную систему т.к. компьютер, моделирующий этот процесс, имеет только один процессор, т.е. может в данный момент решать только одну задачу.
|
При численном моделировании для построения компьютерной модели используются методы вычислительной математики, а вычислительный экспе- римент заключается в численном решении некоторых математических уравне- ний при заданных значениях параметров и начальных условий. Имитационное моделирование (ИМ) — это вид компьютерного модели- рования, для которого характерно воспроизведение на ЭВМ (имитация) процес- са функционирования исследуемой сложной системы. При этом имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры, последовательности протекания во времени, что позволяет получить информацию о состоянии системы S в заданные моменты времени. При отсутствии в моделируемой системе случайных элементов, после определения начальных условий достаточно одного прогона модели, поскольку все остальные прогоны будут развиваться аналогично. Если же в моделируемой системе присутствуют случайные элементы, то каждый новый прогон модели такой системы может «развиваться» иначе, чем предыдущие. В этом случае нас, как правило, не будут интересовать результаты отдельного прогона, а некоторые обобщенные (статистические) характеристики по всем прогонам. Статистическое моделирование (СМ) — это вид имитационного моделирования, включающий моделирование случайных элементов, позволяющий получить статистические данные о процессах в моделируемой системе S. Преимущества математического моделирования 1. Объединение достоинств традиционных теоретических и экспериментальных методов. 2. Исследование таких систем, натурное и физическое моделирование кот невозможно или экономически не оправдано. 3. Исследование труднодоступных объектов удаленных в пространстве и времени, а также объектов ненаблюдаемых, вследствие их размеров и времени существования. Основным недостатком математического моделирования является проблема адекватности построенной модели реальной системе.
|
||||||||||||||||||||||||||||||||
Недостатки ИМ: 1) результаты имитационного моделирования обладают меньшей степенью общности по сравнению с АМ и не позволяют выявить общие закономерности функционирования классов систем; 2) не существует надёжных методов оценки адекватности ИМ.
|
В процессе функционирования агрегата происходят изменения его состояния в соответствии с законом функционирования, определяемым оператором Н(⋅). В моменты наступления ОС функция Н(⋅) изменяется скачкообразно (т.е. функция Н(⋅) имеет разрывы). Во временных интервалах между моментами наступления ОС функция Н(⋅) является непрерывной.
|
Поток
{ Приборы связаны и взаимодействуют между собой. Если каналы { } различных приборов соединены параллельно, то имеет место многоканальное обслуживание. Если же приборы { } или их параллельные блоки соединены последовательно, то говорят о многофазном обслуживании. Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом. A / B / n / m , где A — характ-ет входной поток (GI — рекуррентный поток; M — простейший поток с показат. Распред. вероятностей; Ek — поток Эрланга k-го порядка; D — регулярный или детерминирован. поток с постоянным интервалом между моментами поступления заявок). B — характер-ет случ последовательности длительностей обслуживания на отдельных каналах (GI или G — рекуррентное обслуживание с одной и той же ф-ей распределения B(t) для разных каналов; M — показательное обслуживание; Ek — эрланговское обслуживание k-го порядка; D — регулярное обслуживание). n — кол-во обслуживающих каналов, m — кол-во мест для ожидания в очереди. Если n > 1, то система наз многоканальной. Значение m = 0 характеризует СМО с потерями; m = ∞ — систему с ожиданием; 0 < m < ∞ — систему с ограниченным числом мест для ожидания. Рекуррентным потоком наз поток заявок для кот хар-но одинак. расределение интегралов времени между последов. заявками. Простейшим наз поток, кот явл рекуррентным, но интервал междусоседними заявками описыв. показательное распределение |
Частные
случаи.
1) Если
Рассмотрим пример — Y-детерминированный автомат при X = {0..4}, Y = {0, 1} и фиксированном входном сигнале { }
|
||||||||||||||||||||||||||||||||
9. Этапы имитационного моделирования Процесс имитационного моделирования СС S можно условно разделить на три последовательно выполняемых этапа: Э1. Построение математической (концептуальной) модели S′; Э2. Разработка моделирующего алгоритма и построение имитационной модели S′′; Э3. Исследование системы S с помощью модели S′′. Этап 1. (переход S → S′) Концептуальная модель S′ сложной системы S представляет собой упрощенное математическое или алгоритмическое описание СС. Построение S′ включает 5 этапов. 1.1. Постановка задачи и формулировка целей исследования. 1.2. Анализ системы S: разбиение системы на элементы, допускающие удобное математическое или алгоритмическое описание; определение связей между элементами. 1.3. Определение параметров, переменных и пространства состояний системы S, т.е. характеристик θ, v, u, y, x; установление областей изменения для каждой характеристики: Θ, V, U, Y, X. 1.4. Выбор показателей эффективности функционирования (вектора w). 1.5. Описание концептуальной модели S′ системы S и проверка её адекватности. Этап 2. (переход S′ → S′′) 2.1. Выбор способа имитации, а также вычислительных и программных средств реализации ИМ. 2.2. Построение логической схемы моделирующего алгоритма. 2.3. Алгоритмизация математических моделей, описывающих поведение элементов системы и связей между ними в рамках выбранного способа имитации.
|
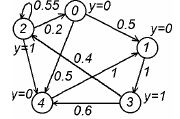
10. Принципы моделирования на ЭВМ случайных элементов. Базовая случайная величина и ее свойства На функционирование реальных сложных сис-м оказывают случайные факторы, которые в математическом моделировании сис-м рассм-ся либо как входные (управляющие) сигналы u, либо как неконтролируемые воздействия внешней среды v. При построении имитационного моделирования системы S возникает необходимость в имитации случайных факторов по заданным законам распределения вероятностей. Объектом имитации м/б не только случайные величины, но и случайные события, векторы, процессы, поля, множества, т.е. произвольные случайные элементы. Моделирование на ЭВМ случайного элемента подчиняется двум основным принципам: 1) сходство между случайным элементом-оригиналом S* и его моделью S состоит в совпадении (близости) вероятностных законов распределения или числовых характеристик; 2) всякий случайный элемент S определяется как некоторая борелевская функция от простейших случайных элементов, так называемых базовых случайных величин (БСВ). В качестве БСВ выбирается непрерывная случайная величина α равномерно распределенная на полуинтервале [0, 1). Функция распределения БСВ
а плотность распределения определяется формулой:
|
11. Методы имитации базовой случайной величины. Их достоинства и недостатки Датчик БСВ — это устройство, позволяющее по запросу получить реализацию α. Существует три типа датчиков: 1) табличный; 2) физический; 3) программный. Табличный датчик БСВ — это таблица случайных чисел, представляющая собой экспериментально полученную выборку реализаций равномерно распределенной в [0, 1) случайной величины. Достоинства: учитывает качественный подбор случ.чисел получаем. качественной реализацией. Недостатки метода: 1) нехватка табличных случайных чисел (часто для моделирования требуются миллионы случайных чисел); 2) большой расход оперативной памяти ЭВМ для хранения таблицы. Физический датчик БСВ — это специальное радиоэлектронное устройство, являющееся приставкой к ЭВМ, выходной сигнал которого имитирует БСВ. Он состоит из источника флуктуационного шума (например “шумящей” радиолампы) и нелинейного преобразователя. Достоинства: практически неограничен. Кол-во реализаций без закцикливания. Недостатки физического датчика БСВ: 1) невозможность повторения некоторой ранее полученной реализации α. 2) схемная нестабильность, приводящая к необходимости контроля работы датчика при очередном его использовании. Программный датчик БСВ — это программа, служащая для имитации на ЭВМ реализаций БСВ. В основе программной имитации лежит рекуррентное преобразование αi = φ(αi-1, αi-2, …,αi-n).
|
12. Методы построения программных датчиков базовой случайной величины Каждая реализация БСВ α есть вещественное число в полуинтервале [0, 1). Большинство известных методов построения БСВ основан на предварительном получении реализации целого числа α*, которое принимает случайные значения на интервале [0, M – 1], где M — так называемый «модуль» ограничивающий числа α*. Тогда i-я реализация БСВ получается по формуле αi = α*i / M . 1. Мультипликативный (конгруэнтный) метод (метод вычетов).Согласно этому методу псевдослучайная последовательность вычисляется по рекуррентным формулам:
α*i
=
(β
α*i-1
) mod
M
(i
=1,2,...),
где α*0
, β,
M
—
параметры программного датчика
(натуральные числа). α*0
— стартовое значение, β
—
постоянный множитель, M
—
модуль ограничивающий числа α*i
(из формулы видно, что α*i
Очевидно, что последовательность {α*i}, а следовательно и {αi} — ограничены кол-вом не превышающем M–1. Отсюда следует, что последовательность реализаций БСВ всегда зацикливается, т.е. начиная с некоторого номера i последовательность повторит прежде уже имеющееся значение с номером j (i > j) αi = αj, а значит: αi+1 = αj+1, αi+2 = αj+2 и т.д. Интервал T = i – j наз. периодом последовательности. Параметры α*0 , β, M выбираются из условия максимума периода. Для 32 разрядных компьютеров рекомендуются следующие: α*0 — нечетное (12345), β = 216 + 3 = 65539, M = 231 = 2147483648. Период данного датчика T ≈ M / 4. 2. Метод использующий линейные смешанные формулы При этом методе псевдослучайная последовательность вычисляется рекуррентно по формуле: αi = α*i / M , α*i = (β1 α*i-1 +...+ βp α*i-p + c) mod M (i = 1, 2,...). |
||||||||||||||||||||||||||||||||
13. Моделирование дискретных случайных величин и случайных событий Дискретная случайная величина (СВ) – СВ, кот принимает отдельные возможные значения xi, i=от 1 до n или i=от 1 до бесконечности с определенными вероятностями. Моделирование дискретных случайных величин(СВ).
Пусть
Алгоритм: ШАГ 1. Моделирование с помощью датчика БСВ реализации α.
ШАГ
2. Принять
решение о том, что реализацией
является х, определяемое по правилу:
Моделирование случайных событий(СС) из полной группы. Система подмножеств F1, F2, …, FN называется полной группой СС на (Ω, F, P) (где F – σ-алгебра подмножеств на Ω), если:
А)
|
14.Моделирование процесса случайного блуждания
Пусть
где
Пусть
в моментt
Определяемый
таким образом случайный процесс
известен как
процесс случайного блуждания на
прямой.
Справедливо также представление
где
Р{ Процесс случайного блуждания может быть определен и для многомерного пространства.
|
15. Метод обратной функции моделирования непрерывной случайной величины При построении ИМ часто возникает необход моделирования непр. СВ с заданной плотностью распределения f (x). В некот случаях для решения данных задач применяется. метод обратной ф-ии.
Функция
распределения случайной величины ξ*
определяется как:
Теорема.
Если α — БСВ, то СВξ= Доказательство. Поскольку при строго монотонном преобразовании F(x) знак нер-ва сохраняется, то из (3.5) и (3.1) получаем:
Моделирующий алгоритм включает следующие этапы: 1) нахождение функции распределения F(x) по заданной плотности распределения согласно (3.3);
2)
нахождение обр ф-и
3) мод-ие реализации БСВ α и выч-ие реализ ξ по (3.5).
Коэффициент
использования БСВ κ =1 . Недостатком
метод являются аналитические трудности
на первых двух этапах. В чистом виде
метод обратной функции применяется
редко т.к. для многих распределений
даже F(x) (не говоря уже о
)
не выражается через элементарные
функции, а табулирование
дополняют
аппроксимациейF(x) или сочетанием с
другими методами.
Метод обратной
функции применим и для моделирования
случайногоN -вектора ξ*=(
Для
СВ ( а)
условные плотности распределения
при условии,что
|
16. Метод Неймана моделирования непрерывной случайной величины
В
случаях, когда плотность распределения
Метод Неймана является приближенным методом, позволяющим получить значения СВ в соответствии с заданным законом распределения. Для применения этого метода достаточно двух условий: 1) интервал (a, b), на котором распределена случайная величина - конечен;
2)
плотность распределения ограничена
сверху
На рис. изображена функция плотности распред. СВ Y, заданная на интервале (a, b). Максимальное значение функции f(y) обозначено W .
|
||||||||||||||||||||||||||||||||
Параметры датчика: p — порядок; α*-p+1 , α*-p+2 , …., α*-1, α*0 — стартовые значения; β1,…βp — множители; c — приращение; M — модуль. Период этого датчика T ≤ Mp – 1, т.е. растет с увеличением p. 3. Метод, использующий нелинейные рекуррентные формулы Иногда псевдослучайная последовательность генерируется с помощью квадратичного рекуррентного соотношения: αi = α*i / M , α*i =(γ (α*i-1 )2 + β α*i-1 + c) mod M (i = 1, 2,...) Параметры α*0, γ, β целесообразно выбирать по следующим правилам. Если M = 2q, то наибольший период достигается только тогда, когда β и c — нечетные γ — четное, причем (β) mod 4 = (γ + 1) mod 4. 4. Метод Макларена-Марсальи Метод основан на комбинации двух простейших программных датчиков БСВ. Пусть {bi} и {сi} (i = 0, 1, 2, …) — псевдослучайные последовательности, порождаемые независимо работающими программными датчиками Д1 и Д2 соответственно. V = {V0, V1, … , VK – 1} последовательность K чисел из {bi}. Результирующее значение БСВ αj является результатом последовательности операций s = [сj K], αj = Vs . Т.о. Д2 осуществляет случайный выбор из последовательности V. Этот метод позволяет ослабить зависимость между членами αj и получать «невероятно» большие периоды, если периоды Т1 и Т2 последовательностей {bi} и {сi} — взаимно простые числа |
Т.е. по происхождению эти числа не случайные, т.к. получаются по детерминированному закону, но по вероятностным характеристикам эти числа похожи на реализации независимых БСВ.
|
Математическое ожидание (первый начальный момент) БСВ M(α) = 1/2, а ее дисперсия (второй центральный момент) σ2(α) = 1/12. Наряду с простейшим экспериментом будем рассматривать составной случайный эксперимент получающийся в результате r-кратного (r ≥ 1) повторения независимо друг от друга простейших экспериментов. Результатом составного случайного эксперимента является последовательность из r независимых БСВ α1, …, αr Согласно второму принципу моделирования случайных элементов случайный элемент θ представляется для некоторого натурального r в виде функции f (·) от r независимых БСВ: θ = f (α1, … , αr). Для имитации одного и того же случайного элемента θ* м/б предложено несколько вариантов функциональных преобразований f(·). Обычно предпочтение отдается варианту f(·), требующему меньше вычислительных затрат. Для этого вводится понятие коэффициента использования БСВ. Коэффициентом использования БСВ κ назовем величину, обратную числу r базовых случайных величин, используемых при моделировании одной реализации случайного элемента θ (κ = 1/r)). Целесообразно выбирать такую функцию f(·), для которой κ принимает наибольшее значение |
2.4. Программирование моделирующего алгоритма. 2.5. Отладка, тестирование и проверка адекватности ИМ. Этап 3. Использование ИМ осуществляется в три этапа. 3.1. Планирование имитационных экспериментов. 3.2. Проведение имитационных экспериментов. 3.3. Обработка, анализ и интерпретация результатов моделирования |
||||||||||||||||||||||||||||||||
Алгоритм метода:
Если
неравенство выполнено, то
|
б)
соответствующие условные функции
распределения:
в)
обратные функции
Тогда
если
………………………
имеет
плотность распределения
Если
Из
курса теории вероятностей известно,
что случайная
величина
Т.о.имеявозможностьполучатьреализацииСВ можнополучитьиз них, используя (3.6) реализации произвольных нормально распределенных СВ с любыми заданными µ и σ. |
|
Б)
В)
Для
моделирования события из полной
группы СС F1,
F2,
…, FN
может
быть применен алгоритм моделирования
дискретной СВ. Обозначим
|
||||||||||||||||||||||||||||||||
17. Метод суперпозиции в моделировании непрерывной случайной величины Книга
Пусть
задана СВ ξ (кси), имеющая плотность
распределения fξ(x).
Введем дополнительную СВ
Если
есть возможность получать реализации
СВ
и условная плотность f(x|y)
позволяет использовать метод обратной
функции, то СВ ξ можно моделировать
в 2 приема сначала по функции
распределения
Если
существует плотность
Если
принимает только целые неотрицательные
значения с вероятностями
Интернет Применим
в случае, если
Тогда моделирование производится следующим образом:
|
18. Применение ЦПТ для моделирования нормально распределенной случай- ной величины Рассмотрим
сумму n независимых БСВ
Математическое
ожидание СВ η равно нулю, а ее дисперсия
равна n. Нормируя эту сумму получим
СВ
Согласно ЦПТ распределение данной СВ при n→∞ стремится к нормальному.
Чем больше n , тем ближе это распределение к нормпльному. На практике вполне достаточно ограничиться значением n=12.
Для
получения реализации СВ распределенной
по нормальному закону с математическим
ожиданием
|
19. Метод Монте-Карло. Это численный метод исследования математических моделей, основанный на моделировании случайных элементов и последующем статистическом анализе результатов моделирования. Особенности: метод численный, поэтому сравнивать по эффективности нужно с численными(приближ.); требует меньше вычислительных затрат по сравн. с др.; позволяет исслед. разные математические модели, не обязательно вероятностные; иногда явл. единственным возможным методом исследования. Суть метода: Необходимо вычислить скал. величину , зад. математическим выражением. Шаг
1:
выбираем
такую, что
Шаг
2: моделируем
Шаг
3: строим
выборочную оценку
Оценим
погрешность метода. Известно, что
последовательность независимых
одинаково распр. случ. величин с кон
дисперсиями подчиняется ЦПТ.
Следовательно,
Если
|
20.
Оценка
площади фигур методом Монте-Карло.
Требуется вычислить площадь
Шаг
1:Обл.
А погружается в обл. G с площадью
Шаг
2: Строится
СВ Бернули
Шаг
3: Методами
имитационного моделирования
генерируется
независимых реализаций
Для
вычисления вел
возможны разл. варианты построения
СВ
,
удовл. условиям:
1)
Дисперсия
2) Моделирование осущ с пом. простого алгоритма.
|
||||||||||||||||||||||||||||||||
21. Вычисление определенного интеграла методом Монте-Карло Рассмотрим
задачу приближенного вычисления
определенного интеграла
где
- Кроме
СВ
рассмотрим
СВ
вида
При
этом
fn> 0, x е [xbx2], ffn (x)dx — 1. Т.о.
согласно (1) построили СВ
,
удовлетворяющую условию Статистика
при n
P{
|
22.Методы повышения точности числ интегрирования методом Монте-Карло Вероятная
ошибка метода Монте-Карло
пропорциональна Выделение главной части Пусть необходимо вычислить интеграл, представимый в виде I
=
Пусть
имеется функция h(x),
близкая к g(x),
такая, что значение интеграла известно,
т.е. вычисляется аналитически или
численно с большой точностью. Тогда
математическое ожидание СВz
= C
+ f(ξ)
- h
(ξ )равноM(
z)
= C
+ I
- C,следовательно,
в качестве приближенного значения
интеграла можно взять значение Если
I
|
23 Решение системы алгебраических уравнений методом Монте - Карло Пусть система алгебраических уравнений задана в виде x = Ax + f ,(1) где x x xn = ( ,..., )T 1 — вектор-столбец неизвестных; f f fn = ( ,..., )T 1 — вектор правых частей A aij = ( ), i, j =1,n – матрица системы. Предположим, что наибольшее по модулю характеристическое число матрицы A меньше единицы, так что сходится метод последовательных приближений (метод простых итераций) x(k) = Ax(k–1) + f , k = 1, 2, … Достаточным условием для того, чтобы все характеристические числа матрицы A лежали внутри единичного круга на комплексной плоскости, т.е. чтобы
|λi|
<
1,
i
=1,
n
,
может служить, например, неравенство
|
24 Решение дифференциальных уравнений 2-го порядка Лапласа и Пуасона методом Монте-Карло В
ограниченной связной области G
двумерной
плоскости с простой границей Г
рассмотрим дифференциальное уравнение
с частными производными
|
||||||||||||||||||||||||||||||||
|
При
достаточно больших значениях
,
Пусть
Несмещенная
оценка дисперсии:
Вероятная
ошибка метода:
|
|
Пример.
Гиперэкспоненциальное распределение.
Моделирование:
|
||||||||||||||||||||||||||||||||
Оказывается,
что все характеристические числа
такой матрицы по абсолютной величине
меньше единицы. Свободные члены
системы (5) равны
|
Рассмотрим
траекторию цепи Маркова длины N
>
0. Объект, переходы которого описываются
цепью Маркова назовем частицей.
Движущейся частице припишем т.н. «вес»
|
Интегрирование по части области Рассм
многомерный интеграл |
Представим
искомый интеграл в виде суммы I=
Для вычисления интеграла можно использовать следующее приближенное значение
|
Из последнего соотношения следует, что отклонение от а тем меньше, чем меньше дисперсия D( ), определяемая (2). Величина D( ) зависит от выбора СВ . До сих пор мы считали, что — произвольная СВ с плотностью распределения удовлетворяющая (3) и (4). Какой же должна быть плотность распределения (x), чтобы дисперсия D( ) была минимальной? Можно
доказать что если ввести величину
В приложениях однократные интегралы вида (6) обычно вычисляются с помощью квадратурных формул, т.е. метод Монте-Карло используется редко, но при переходе к многократным интегралам квадратурные формулы становятся очень сложными, а метод Монте-Карло почти не усложняется.
|
||||||||||||||||||||||||||||||||
25. Статистический анализ результатов моделирования Пусть ξ есть случайная величина с функцией распределения F(x) = P{ξ < x}, являющаяся математической моделью единичного наблюдения одной из компонент, используемых в ходе имитационного моделирования. Наибольшее распространение на практике имеют два класса функций распределения F(x): 1) абсолютно-непрерывные и 2) дискретные. В первом случае существует плотность распределения вероятностей СВ: f (x) = dF(x) / dx. (6.1) Во втором случае СВ ξ, принимает значения из дискретного множества {x1, x2 ,…}и имеет дискретное распределение вероятностей pj = P(ξ = xj ) . (6.2) Вероятностная модель наблюдения ξ, полностью описывается функциональными характеристиками: ф-й распределения F(x), плотностью распределения (6.1) или дискретным распределением вероятностей (6.2). В случаях, когда получить полное вероятностное описание не возможно или нецелесообразно, на практике используются числовые харак-ики. Любая числовая характер-ка λ является некоторым функционалом от F(·): λ = λ(F(·)) .Мн-тво числовых характеристик состоит из двух след. подмн-тв. I. Числовые характеристики среднего: — математическое ожидание (среднее) M{ξ} = μ; — медиана Me{ξ} = Me : F(Мe) = 1/2; — мода (для НСВ) Mo{ ξ } = Mo = arg max x f (x) — наибольшее а+ и наименьшее а– значения,
P{a−
≤ ξ ≤ a+}
≡
1,
P{a−
+ ε ≤ ξ ≤ a+
− ε}
<
1,
II. Числовые характеристики рассеяния: — дисперсия D{ξ} = D = M{(ξ − μ)2};
— среднеквадратическое
(стандартное) отклонение σ{ξ}
=
σ =
— размах а = а+ – а–; — коэффициент асимметрии As = M{(ξ − μ)3} σ3 ; — коэффициент эксцесса (островершинности) Ex = M{(ξ − μ)4} σ4 − 3.
|
26. Проверка адекватности моделей. При имитации различных случ. факторов, присутств. в исслед. системе, а также при вероятностно-стат-ском описании рез-тов моделирования возникает след. задача проверки адекватности моделей данных.
Пусть
ре-ты модел-ия (данные) Z
= (
Статистикой
для рассм. задачи проверки адекватности
модели наз. стат.
Стат.(1)
хар-т взвешенную сумму квадратов
уклонений относит. частот
- критерий основан на (1) и имеет вид:
гипотеза
приним.:
или в альтернативной форме:
гипотеза
приним.:
где
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
При
увел-нии числа прогонов n
гарантируется
заданный уровень надежности решений.
Чтобы повысить скорость сход-ти вер-ти
ошибки 1-го рода
-критерий справедлив и для проверки адекватности многомерных данных ξ∈ , N > 1.
Критерий
согласия Колмогорова.
Пусть
по рез-там модел-ия Z
вычислена
выбор. ф-ия распр-ия
Если
верна
Ценность
этого св-ва состоит в том, что
Сход-ть
(2) — достаточно быстрая, и ф-ию распр.
Колмогорова K(⋅)
рекоменд. использовать начиная с
n>20.
Поэтому крит. согл. Колм., основан. на
св-ах стат-ки
принимается
гипотеза
или в эквивалентной форме (с испол. P-значения):
принимается
гипотеза
где
|
В процессе моделирования функциональные и числовые характеристики вероятностного распределения часто неизвестны и возникает задача их статистического оценивания по случайной выборке Z = (z1, z2, ... , zп). Выборочная (эмпирическая) функция распределения:
В
случае дискретной вероятностной
модели (6.2) относительная частота —
В случае абсолютно-непрерывной вероятностной модели (6.1) для оценивания плотности f(·) обычно применяется гистограмма. Для ее построения разобьем промежуток [а–, а+] плотности f(·) на L ячеек точками деления b0 < b1 < … < bL: b0 = а–, bL = а+.
Обозначим
Эта оценка является смещенной и несостоятельной в общем случае, поэтому обычно используется лишь для визуализации результатов моделирования.
Cтатистическая
оценка мат.ожидания примет вид:
Кроме точечных оценок м/б построены интервальные оценки. Например, если L{ξ} = N{μ, D}, то для μ справедливы интервальные оценки:
где
ε
—
доверительный уровень (уровень
значимости),
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||

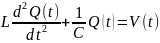 (1)
(1)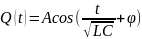 ,
где A — амплитуда, ϕ — начальная фаза
колебаний.
,
где A — амплитуда, ϕ — начальная фаза
колебаний.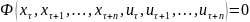 (1)
где
(1)
где
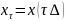 ,
,
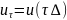 —
соответственно состояние системы и
внешнее воздействие в дискретный
момент времени τ. ДД-модели в виде
(1) часто возникают как промежуточные
при исследовании НД-моделей на ЭВМ,
когда аналитическое решение
дифференциального уравнения получить
не удается и приходится применять
разностные схемы.
—
соответственно состояние системы и
внешнее воздействие в дискретный
момент времени τ. ДД-модели в виде
(1) часто возникают как промежуточные
при исследовании НД-моделей на ЭВМ,
когда аналитическое решение
дифференциального уравнения получить
не удается и приходится применять
разностные схемы.
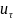 }.
}.
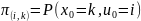 — начальное
распределение вероятностей;
— начальное
распределение вероятностей;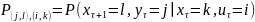 — вероятность
события, состоящего в том, что
находящийся в τ-м такте в состоянии
— вероятность
события, состоящего в том, что
находящийся в τ-м такте в состоянии
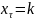 автомат под действием сигнала
автомат под действием сигнала
 выдаст сигнал
выдаст сигнал
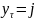 и перейдет в состояние
и перейдет в состояние

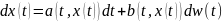 ,
где
,
где
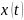 — случайный процесс, определяющий
состояние системы в момент времени
t;
— случайный процесс, определяющий
состояние системы в момент времени
t;
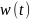 — стандартный винеровский случайный
процесс; b(⋅) и а(⋅) и — коэффициенты
диффузии и переноса. При некоторых
условиях гладкости на
— стандартный винеровский случайный
процесс; b(⋅) и а(⋅) и — коэффициенты
диффузии и переноса. При некоторых
условиях гладкости на
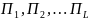 .
Прибор
.
Прибор
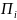 состоит
из накопителя заявок
состоит
из накопителя заявок
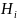 ,
в котором могут находится одновременно
,
в котором могут находится одновременно
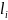 заявок (0 ≤
≤
заявок (0 ≤
≤
 )
и канала
)
и канала
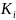 обслуживания заявок (
— емкость накопителя
).
На каждый прибор
поступают потоки событий (заявок).
Поток заявок представляет собой
последовательность интервалов между
моментами появления заявок на входе
и образует подмножество неуправляемых
переменных СМО.
обслуживания заявок (
— емкость накопителя
).
На каждый прибор
поступают потоки событий (заявок).
Поток заявок представляет собой
последовательность интервалов между
моментами появления заявок на входе
и образует подмножество неуправляемых
переменных СМО.
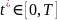 находится
в ОС, если
находится
в ОС, если
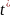 — либо момент поступления воздействия
внешней среды
— либо момент поступления воздействия
внешней среды
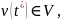 либо
момент поступления управляющего
сигнала
либо
момент поступления управляющего
сигнала
 ,либо
момент выдачи выходного сигнала
,либо
момент выдачи выходного сигнала
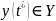 . Все остальные состояния А называются
неособыми состояниями.
. Все остальные состояния А называются
неособыми состояниями.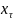 ∈
X, поступает входной сигнал
∈
U, на который автомат реагирует
переходом на такте τ + 1 в состояние
∈
X, поступает входной сигнал
∈
U, на который автомат реагирует
переходом на такте τ + 1 в состояние
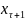 ∈
X и выдачей выходного сигнала
∈
X и выдачей выходного сигнала
 ∈
Y
∈
Y
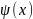 -ф-ия
выходов КА
-ф-ия
выходов КА –ф-ия
–ф-ия
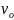 – нач. скорость,
– нач. скорость,
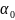 – угол
– угол
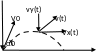
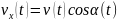 .
Т.к. в горизонтальном направлении на
тело не действ. никакие силы,
эта составляющая скорости не изменится.
.
Т.к. в горизонтальном направлении на
тело не действ. никакие силы,
эта составляющая скорости не изменится.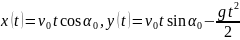 ,
скорость описывется:
,
скорость описывется:
 .
.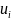 }
представляет собой последовательность
интервалов времени между моментами
начала и окончания обслуживания
заявок и образует подмн-тво управляемых
переменных. Заявки, обслуженные
каналом,
образуют выходной поток {
}
представляет собой последовательность
интервалов времени между моментами
начала и окончания обслуживания
заявок и образует подмн-тво управляемых
переменных. Заявки, обслуженные
каналом,
образуют выходной поток {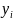 }
— последовательность интервалов
времени между моментами выхода заявок
— выходной сигнал СМО. Процесс
функционирования прибора
можно представить как процесс
изменения состояния во времени
двумерного вектора
}
— последовательность интервалов
времени между моментами выхода заявок
— выходной сигнал СМО. Процесс
функционирования прибора
можно представить как процесс
изменения состояния во времени
двумерного вектора
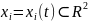 ,
где
,
где
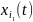 - число
заявок находящихся в накопителе в
момент t;
- число
заявок находящихся в накопителе в
момент t;
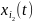 — состояние канала обслуживания
(
— состояние канала обслуживания
( если канал свободен и
если канал свободен и
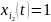 если канал занят).
если канал занят).
 ,
то получаем ДД КА. 2) Если функция
выходов Ψ(x, u) является детерминированной,
а ф-ия переходов
,
то получаем ДД КА. 2) Если функция
выходов Ψ(x, u) является детерминированной,
а ф-ия переходов
 описывается
однородной цепью Маркова с известным
начальным распределением вероятностей,
то такой автомат удобно представить
в виде ориентированного графа,
вершины которого соответствуют
состояниям автомата, а дуги переходам.
Каждая дуга помечается ее весом —
вероятностью соответствующего
перехода, а каждая вершина —
соответствующим значением выходного
сигнала.
описывается
однородной цепью Маркова с известным
начальным распределением вероятностей,
то такой автомат удобно представить
в виде ориентированного графа,
вершины которого соответствуют
состояниям автомата, а дуги переходам.
Каждая дуга помечается ее весом —
вероятностью соответствующего
перехода, а каждая вершина —
соответствующим значением выходного
сигнала.
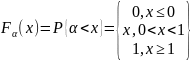
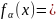
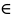 {1,..., M−1}.)
{1,..., M−1}.)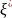 - дискретная СВ, принимающая N<∞
возможных
значений С1<
С2<…<СN
с
заданными вероятностями р1<
р2<…<рN
соответственно.
Для реализации
- дискретная СВ, принимающая N<∞
возможных
значений С1<
С2<…<СN
с
заданными вероятностями р1<
р2<…<рN
соответственно.
Для реализации
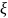 - модели СВ
введем вспомогательный N-вектор:
q=(q1,
q2,
…, qN)=(
p1,
p1+p2,
…, 1).
- модели СВ
введем вспомогательный N-вектор:
q=(q1,
q2,
…, qN)=(
p1,
p1+p2,
…, 1).
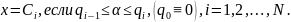
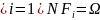 - происходит хотя бы одно событие
группы;
- происходит хотя бы одно событие
группы;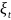 случайный процесс с дискретным
временем t=m
случайный процесс с дискретным
временем t=m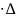 ,
m=0,1,...
и дискретным фазовым пространством
состояний X :
,
m=0,1,...
и дискретным фазовым пространством
состояний X :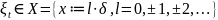
 >
0 - шаги дискретизации времени, а δ>
0 - шаги дискретизации пространства.
>
0 - шаги дискретизации времени, а δ>
0 - шаги дискретизации пространства.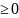 процесс
находится в состоянии .x
X,
т.е.
=
х,
а в следующий момент времени
процесс
находится в состоянии .x
X,
т.е.
=
х,
а в следующий момент времени
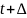 состояние
процесса определяется соотношениями
состояние
процесса определяется соотношениями
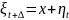
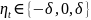 -
дискретная СВ с распределением
вероятностей
-
дискретная СВ с распределением
вероятностей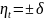 }
= р±,Р{
}
= р±,Р{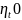 }
=
}
=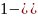 Т.о.
моделирование процесса
сводится
к моделированию в каждый момент
времени
реализации СВ
Т.о.
моделирование процесса
сводится
к моделированию в каждый момент
времени
реализации СВ
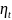 и использовании соотношения (3.3).
и использовании соотношения (3.3).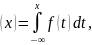 (3.3) , которую будем полагать строго
монотонно возрастающей.Через
(3.3) , которую будем полагать строго
монотонно возрастающей.Через
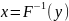 обозначим функцию обратную F(x);
она находится при решении уравнения
F(x)=y.
(3.4)
обозначим функцию обратную F(x);
она находится при решении уравнения
F(x)=y.
(3.4)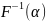 (3.5)
имеет заданную плотность распределения
f
(x).
(3.5)
имеет заданную плотность распределения
f
(x). ,
т.е.
,
т.е.
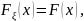 ),
а с учетом (3.3) получаем что
),
а с учетом (3.3) получаем что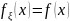 .
.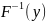 путем
решения ур-ия (3.4);
путем
решения ур-ия (3.4);
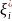 )
)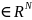 с
заданной плотностью распределения
с
заданной плотностью распределения
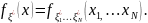 По свойству согласованности многомерной
плотности распределения (k=N−1,N−2,...,1)
По свойству согласованности многомерной
плотности распределения (k=N−1,N−2,...,1)
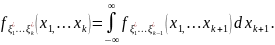
 )
вычислим
)
вычислим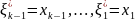 ,
фиксированные:
,
фиксированные:

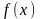 моделируемой
СВ ξ* имеет сложный аналитический вид
и метод обратной функции не применим,
можно использовать метод Неймана
(метод режекции, метод исключения).
моделируемой
СВ ξ* имеет сложный аналитический вид
и метод обратной функции не применим,
можно использовать метод Неймана
(метод режекции, метод исключения).
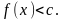

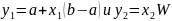
 .
.
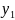 и
есть искомое значение СВ Y.
На рис. это соответствует первой
координате точки B1.
В противном случае СЧ отбрасываются.
Далее вновь генерируются СЧ (x1,
x2)
и алгоритм повторяется.
и
есть искомое значение СВ Y.
На рис. это соответствует первой
координате точки B1.
В противном случае СЧ отбрасываются.
Далее вновь генерируются СЧ (x1,
x2)
и алгоритм повторяется.
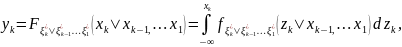 которые будем полагать монотонно
возрастающими по
которые будем полагать монотонно
возрастающими по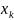 .
.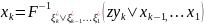 в том числе безусловную обратную
функцию для компоненты
в том числе безусловную обратную
функцию для компоненты
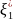 :
: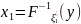
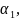 ...,
...,
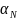 —
независимые в совокупности БСВ, то
случайный вектор ξ=(
—
независимые в совокупности БСВ, то
случайный вектор ξ=(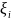 )∈
)∈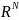 с компонентами
с компонентами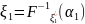 ,
,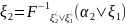 ,
,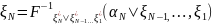
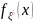 .
Доказательство аналогичное для
одномерного случая начиная с
.
Доказательство аналогичное для
одномерного случая начиная с
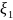 .
.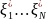 независимы в совокупности, то
моделирование каждой компоненты
может быть осуществлено независимо
от других.
Компоненты ξ*
можно
занумероватьN! способами. Т.е. существует
N! представлений условных плотностей.
Простота реализации алгоритма часто
зависит от того, насколько удобно
выбрано такое представление. Коэффициент
использования БСВ κ=1/ N .
Замечание.Примоделированииреальныхпроцессоводнойизсамых
насущных задач является получение
реализаций случайной величины имеющих
нормальное (гауссовское)распределениеξ
~ N(µ, σ),гдеµ — математическое ожидание
этой случайной величины, а σ — его
среднее квадратическое отклонение.
независимы в совокупности, то
моделирование каждой компоненты
может быть осуществлено независимо
от других.
Компоненты ξ*
можно
занумероватьN! способами. Т.е. существует
N! представлений условных плотностей.
Простота реализации алгоритма часто
зависит от того, насколько удобно
выбрано такое представление. Коэффициент
использования БСВ κ=1/ N .
Замечание.Примоделированииреальныхпроцессоводнойизсамых
насущных задач является получение
реализаций случайной величины имеющих
нормальное (гауссовское)распределениеξ
~ N(µ, σ),гдеµ — математическое ожидание
этой случайной величины, а σ — его
среднее квадратическое отклонение.
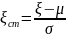 имеетстандартноенормальноераспределение,т.е.
имеетстандартноенормальноераспределение,т.е.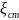 ~ N(0,
1).Тогдаизпростейших преобразований
получим ξ
=
⋅σ
+ µ .
~ N(0,
1).Тогдаизпростейших преобразований
получим ξ
=
⋅σ
+ µ .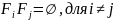 –
совместное наступление 2 или более
СС из группы невозможно;
–
совместное наступление 2 или более
СС из группы невозможно;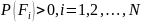 – все СС группы имеют ненулевые
вероятности.
– все СС группы имеют ненулевые
вероятности.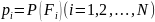 - вероятности i-го
события из группы. Введем дискретную
СВ
,
принимающую значения
- вероятности i-го
события из группы. Введем дискретную
СВ
,
принимающую значения
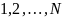 с вероятностями р1,
р2,…,рN
соответственно.
- номер события из полной группы. Тогда
задача моделирования СС сводится к
задаче моделирования СВ
.
с вероятностями р1,
р2,…,рN
соответственно.
- номер события из полной группы. Тогда
задача моделирования СС сводится к
задаче моделирования СВ
.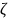 (дзета) с функцией распределения
(дзета) с функцией распределения
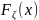 .
Пусть f(x|y)
– условная плотность распределения
СВ ξ при условии
=у.
В этом случае, как известно из теории
вероятностей,
.
Пусть f(x|y)
– условная плотность распределения
СВ ξ при условии
=у.
В этом случае, как известно из теории
вероятностей,
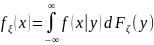 (1).
(1).
 получить реализацию у СВ
,
затем по плотности f(x|y)
моделировать х – значение СВ ξ.
получить реализацию у СВ
,
затем по плотности f(x|y)
моделировать х – значение СВ ξ.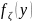 СВ
,
то (1) представимо в виде:
СВ
,
то (1) представимо в виде:
 .
.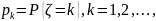 то плотность fξ(x)
представима в виде:
то плотность fξ(x)
представима в виде:
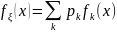 ,
где
,
где
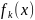 – условные плотности СВ ξ при условии,
что
=k.
– условные плотности СВ ξ при условии,
что
=k.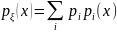 ,
где
,
где
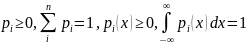 .
.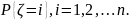
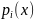 .
.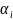 . Поскольку математическое ожидание
каждой из них равно 1/2, а дисперсия
1/12. Введем сумму
. Поскольку математическое ожидание
каждой из них равно 1/2, а дисперсия
1/12. Введем сумму
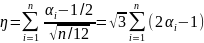
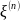 с
мат. ожиданием равным нулю и дисперсией
равной 1.
с
мат. ожиданием равным нулю и дисперсией
равной 1.

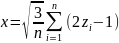 ,
где
-
независимая реализация БСВ
,
где
-
независимая реализация БСВ .
. и средним квадратическим отклонением
σ используют представление ζ=σξ+a
и средним квадратическим отклонением
σ используют представление ζ=σξ+a
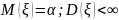
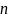 независимых реализаций случ. вел.
независимых реализаций случ. вел.
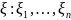 .
.
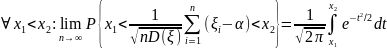 .
.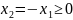 ,
тогда
,
тогда
 ,
где Ф – ф-ция норм распр.:
,
где Ф – ф-ция норм распр.:
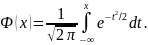
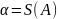 плоской фигуры А.
плоской фигуры А.
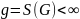 .
.
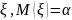 .
.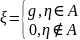 ,
где
,
где
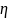 – случайный двумерный вектор равномерно
распр. в обл. G. Обозначим
– случайный двумерный вектор равномерно
распр. в обл. G. Обозначим
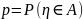 – вероятность соб-я
– вероятность соб-я
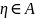 .
Тогда
.
Тогда
 .
.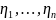 ,
строится случ. выборка
,
строится случ. выборка
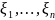 и вычисляется оценка величины
:
и вычисляется оценка величины
:
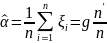 ,
где
,
где
 – число реализаций из
– число реализаций из
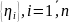 ,
попавших в обл. А, т.е.
,
попавших в обл. А, т.е.
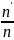 – относительная частота попаданий
(эффективная оценка вероятности
– относительная частота попаданий
(эффективная оценка вероятности
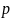 ).
).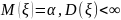 .
Предпочтение отдается варианту,
удовл. условиям:
.
Предпочтение отдается варианту,
удовл. условиям: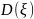 минимальна на мн-ве СВ
.
минимальна на мн-ве СВ
.
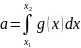 (6)
(6)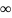 <
g(x) <
— некоторая, определенная на интервале
[x1, x2] функция. Выберем произвольную
СВ
с плотностью распределения
<
g(x) <
— некоторая, определенная на интервале
[x1, x2] функция. Выберем произвольную
СВ
с плотностью распределения >0,
x
>0,
x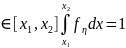 (3)
(3)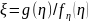 (1),
причём
g(x)
и
(1),
причём
g(x)
и
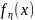 должны быть такими,что:
должны быть такими,что: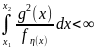 (4)
Тогда
(4)
Тогда

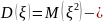 (2)
(2)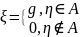 .
Поэтому
в качестве приближенного значения
величины а можно использовать
статистическую оценку
.
Поэтому
в качестве приближенного значения
величины а можно использовать
статистическую оценку
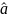 ,
построенную по выборке из n независимых
СВ
,
i = 1, n.
,
построенную по выборке из n независимых
СВ
,
i = 1, n.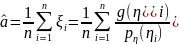
 да имеет асимптотически нормальное
распределение, и вероятность отклонения
от а, согласно ЦПТ, удовлетворяет
соотношению
да имеет асимптотически нормальное
распределение, и вероятность отклонения
от а, согласно ЦПТ, удовлетворяет
соотношению
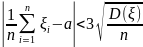 }
}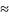 0,997
0,997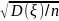 .Скорость
убывания этой ошибки с ростом n
невелика. Поэтому важно выбирать для
расчета интегралов вычислительные
схемы или, т.е. такие случайные
величины
,
для которых дисперсия D(
)
мала. Способы построения таких схем
наз методами понижения дисперсии.
Метод существенной выборки один из
таких методов. Рассмотрим другие
наиболее часто встречающиеся на
практике методы.
.Скорость
убывания этой ошибки с ростом n
невелика. Поэтому важно выбирать для
расчета интегралов вычислительные
схемы или, т.е. такие случайные
величины
,
для которых дисперсия D(
)
мала. Способы построения таких схем
наз методами понижения дисперсии.
Метод существенной выборки один из
таких методов. Рассмотрим другие
наиболее часто встречающиеся на
практике методы.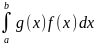 ,
p(x) > 0,
,
p(x) > 0,
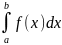 =
1.
=
1.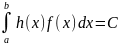
 =
C
+ 1/n
=
C
+ 1/n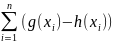 ,где
,где
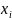 — i-ая
реализация СВ ξ с плотностью
распределения f(x),
n
— число реализаций. Оценим дисперсию
случайной величины z:
D(z)
=
— i-ая
реализация СВ ξ с плотностью
распределения f(x),
n
— число реализаций. Оценим дисперсию
случайной величины z:
D(z)
=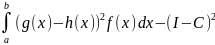 .
. 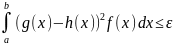 ,
то D(z)
,
то D(z)
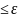 .
.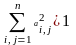 Пологая,
что
Пологая,
что
 ,
то
,
то
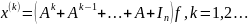 ,
,
 точное
решение системы (1). Рассмотрим
задачу о вычислении скалярного
произведения (h,
точное
решение системы (1). Рассмотрим
задачу о вычислении скалярного
произведения (h,
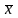 )
,
где h
—заданный
вектор. Будем связывать с системой
(1) и вектором h
некоторую
фиксированную цепь Маркова из множества
цепей, определяемых парой {π,
P}:
)
,
где h
—заданный
вектор. Будем связывать с системой
(1) и вектором h
некоторую
фиксированную цепь Маркова из множества
цепей, определяемых парой {π,
P}:
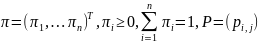 ,
,
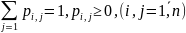 для
которых выполнены условия:
для
которых выполнены условия: Положим
Положим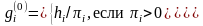
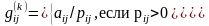 (2)
(2)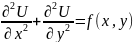 (1)
где U
— неизвестная
функция. Уравнение (1) при f(х,у)
≡
0
называется уравнением Лапласа, а при
f(х,у)
≠
0
— уравнением Пуассона. Предположим,
что на границе Г задана некоторая
функция g(х,у);
U(x,
y)|г
= g(х,у).(2)
Задачу об отыскании решения уравнения
(1), удовлетворяющего граничному
условию (2), называют задачей Дирихле.
Для приближенного решения этой задачи
выбирают на плоскости достаточно
мелкую квадратную сетку с шагом h.
Координаты узлов этой сетки пусть
будут x
=
jh,
yi
= lh,
j,l
=
1,
n,
а значения U(xj,
yl)
и f(xj,
yl)
для краткости обозначим Ujl
и
fjl.
Узел ( j,
l
)
называют внутренним, если он и все
четыре соседних с ним узла принадлежат
G
U
Γ
,
в противном случае узел ( j,
l
),
принадлежащий G
U
Γ
,
называют граничным. Во внутреннем
узле G
U
Γ
уравнение
(1) заменяется разностным уравнением
(1)
где U
— неизвестная
функция. Уравнение (1) при f(х,у)
≡
0
называется уравнением Лапласа, а при
f(х,у)
≠
0
— уравнением Пуассона. Предположим,
что на границе Г задана некоторая
функция g(х,у);
U(x,
y)|г
= g(х,у).(2)
Задачу об отыскании решения уравнения
(1), удовлетворяющего граничному
условию (2), называют задачей Дирихле.
Для приближенного решения этой задачи
выбирают на плоскости достаточно
мелкую квадратную сетку с шагом h.
Координаты узлов этой сетки пусть
будут x
=
jh,
yi
= lh,
j,l
=
1,
n,
а значения U(xj,
yl)
и f(xj,
yl)
для краткости обозначим Ujl
и
fjl.
Узел ( j,
l
)
называют внутренним, если он и все
четыре соседних с ним узла принадлежат
G
U
Γ
,
в противном случае узел ( j,
l
),
принадлежащий G
U
Γ
,
называют граничным. Во внутреннем
узле G
U
Γ
уравнение
(1) заменяется разностным уравнением
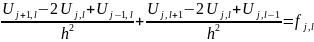 ,
которое можно представить в виде
,
которое можно представить в виде
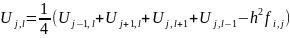 (3)
В граничных узлах (xj,
yl)
полагают Uj,l
= gj,l .
(4) Решение алгебраической системы
(3), (4) при h
→
0
приближается к точному решению задачи
Дирихле для уравнения (1) Если
перенумеровать все узлы, принадлежащие
G
U
Γ
(в
произвольном порядке), и переписать
в том же порядке уравнения (3), (4), то
получим систему линейных алгебраических
уравнений вида x
=
Ax
+
f
,
(3)
В граничных узлах (xj,
yl)
полагают Uj,l
= gj,l .
(4) Решение алгебраической системы
(3), (4) при h
→
0
приближается к точному решению задачи
Дирихле для уравнения (1) Если
перенумеровать все узлы, принадлежащие
G
U
Γ
(в
произвольном порядке), и переписать
в том же порядке уравнения (3), (4), то
получим систему линейных алгебраических
уравнений вида x
=
Ax
+
f
,
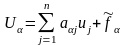 α=1,m
(m–кол-фо
узлов) или в матрияной форме u=Au+f(5)
где матрица A
имеет
следующую структуру; внутреннему
узлу с номером α
отвечает
строка
α=1,m
(m–кол-фо
узлов) или в матрияной форме u=Au+f(5)
где матрица A
имеет
следующую структуру; внутреннему
узлу с номером α
отвечает
строка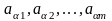 ,
в которой четыре элемента равны 1/4, а
остальные – нули; граничному узлу с
номером α
отвечает
нулевая строка; все диагональные
элементы матрицы
,
в которой четыре элемента равны 1/4, а
остальные – нули; граничному узлу с
номером α
отвечает
нулевая строка; все диагональные
элементы матрицы
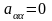 .
.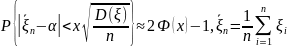 .
.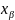 – решение у-ния
– решение у-ния
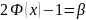 .(*)
Тогда
.(*)
Тогда
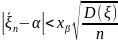 равна
равна
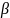 .
.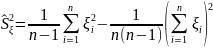 .
. .
Множитель 0,6745 – реш-е у-ния (*) при
.
Множитель 0,6745 – реш-е у-ния (*) при
 .
«Вероятная ошибка», т.к одинаково
веротны ошибки большие чем
.
«Вероятная ошибка», т.к одинаково
веротны ошибки большие чем
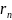 и меньшие
.
и меньшие
.
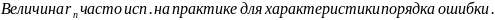
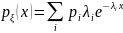
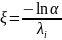 ,
где I
- смоделирована как дискретная
случайная величина
,
где I
- смоделирована как дискретная
случайная величина
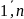 с рядом
с рядом
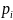 .
. Используя метод из вопроса 23найдем
приближенное значение функции и(х,
у)
в одном (заранее заданном) узле r.
Выберем матрицу вероятностей
одношаговых переходов
Используя метод из вопроса 23найдем
приближенное значение функции и(х,
у)
в одном (заранее заданном) узле r.
Выберем матрицу вероятностей
одношаговых переходов где
где
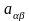 элемент матрицы А,
элемент матрицы А,
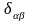 –символ
Кронекера
–символ
Кронекера
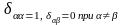 Процесс
построения цепи по такому правилу
состоит из следующихэтапов:1) начинаем
с узла i0
= r;2)
если узел ik
внутренний,
то с одинаковой вероятностью 1/4
выбираем в качестве ik+1
номер одного из соседних с ним узлов;
3) если узел ik
граничный,
то цепь останавливается ik
=
ik+1
= ik+2
= … Расчет весов
Процесс
построения цепи по такому правилу
состоит из следующихэтапов:1) начинаем
с узла i0
= r;2)
если узел ik
внутренний,
то с одинаковой вероятностью 1/4
выбираем в качестве ik+1
номер одного из соседних с ним узлов;
3) если узел ik
граничный,
то цепь останавливается ik
=
ik+1
= ik+2
= … Расчет весов
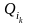 вдоль
такой цепи лчень прост: пока цепь не
попала на границу
вдоль
такой цепи лчень прост: пока цепь не
попала на границу
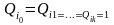 далее
далее
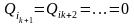 Поэтому
случайная величина ξ
оказывается
равной
Поэтому
случайная величина ξ
оказывается
равной где
где
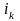 —
номер первого выхода на границу. В
формуле (7) все
—
номер первого выхода на границу. В
формуле (7) все
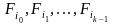 вычисляются
по формуле
вычисляются
по формуле
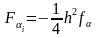 последнее
значение равно
последнее
значение равно
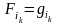
 ,
который изменяется при движении ее
по траектории i0
→
i1
→
…
→
in
по
следующему правилу. В начальный
момент, когда она находится в состоянии
i0,
частица имеет вес
,
который изменяется при движении ее
по траектории i0
→
i1
→
…
→
in
по
следующему правилу. В начальный
момент, когда она находится в состоянии
i0,
частица имеет вес при переходе из состояния i0
в i1
ее «вес» становится равным
при переходе из состояния i0
в i1
ее «вес» становится равным
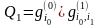 и
т.д т.е
и
т.д т.е
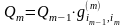 (3)Введем
случайную величину
(3)Введем
случайную величину
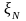 ,
определенную на траектории марковской
цепи длины N
,
определенную на траектории марковской
цепи длины N
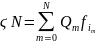 .
Используя
формулу умножения вероятностей,
найдем
.
Используя
формулу умножения вероятностей,
найдем
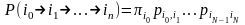 Из
последнего выражения и формулы (2)
можно получить математическое ожидание
СВ ξN
Из
последнего выражения и формулы (2)
можно получить математическое ожидание
СВ ξN
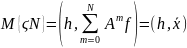 (4)
Для
получения приближенного значения
(4)
Для
получения приближенного значения
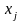 —
j-ой
компоненты вектора
удобнее
всего выбрать в качестве h
единичный
вектор
—
j-ой
компоненты вектора
удобнее
всего выбрать в качестве h
единичный
вектор
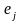 =(0,0,...,0,1,0,...0)^T
,
в котором лишь на j-ом
месте стоит единица. Тогда скалярное
произведение (4) равно xj
.Затем
моделируем l
реализаций
цепи Маркова:
=(0,0,...,0,1,0,...0)^T
,
в котором лишь на j-ом
месте стоит единица. Тогда скалярное
произведение (4) равно xj
.Затем
моделируем l
реализаций
цепи Маркова: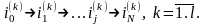 Вычисляем вдоль этих цепей «веса»
Вычисляем вдоль этих цепей «веса»
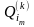 по
формуле(3) тогда
по
формуле(3) тогда
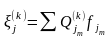 Приближенное значение для хj
имеет вид
Приближенное значение для хj
имеет вид

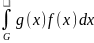 ,
G
,
G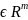 , где функция f(x)обладает
свойством
, где функция f(x)обладает
свойством
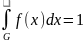 .
Предположим, что можно аналитическивычислить
данный интеграл по некоторой части
B
области G:
.
Предположим, что можно аналитическивычислить
данный интеграл по некоторой части
B
области G:
 ,
,
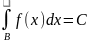 ,
0 <C<
1.
,
0 <C<
1.
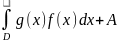 ,где
D
= G
/ B.
В области D
определим плотность
,где
D
= G
/ B.
В области D
определим плотность
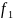 (x)
= f
(x)/(1
- C).
Рассмотрим СВ
(x)
= f
(x)/(1
- C).
Рассмотрим СВ = A
+ (1 –C)f(
),
где ξ — СВ с плотностью
(x).
Тогда математическое ожидание СВ w
равно I.
= A
+ (1 –C)f(
),
где ξ — СВ с плотностью
(x).
Тогда математическое ожидание СВ w
равно I.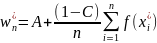 ,
где
,
где
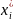 ,
i=1,n-реализации
СВ, распределенной в облD
с плотностью
(x).
Можно показать, что D(
,
i=1,n-реализации
СВ, распределенной в облD
с плотностью
(x).
Можно показать, что D(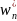 )
<D(
)
<D(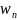 ),
где
=
1/n
),
где
=
1/n ,
,
i
=1-реализации СВ с плотностью f(x).
,
,
i
=1-реализации СВ с плотностью f(x).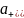 ,
определяемую как
,
определяемую как
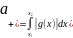 ,
то дисперсия случайной величины
,
удовлетворяет соотношению D(
)
,
то дисперсия случайной величины
,
удовлетворяет соотношению D(
)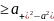 и
достигает минимума при условии
(x)=
и
достигает минимума при условии
(x)= (5).
Данный метод получил название метода
существенной выборки. Замечание.
Выбрать наилучшую плотность
(x),
заданную формулой (5), на практике
часто невозможно, т.к. возможность
получить значение величину
,
как правило не выше чем значение
искомой величины а. Поэтомуна практике
ограничиваются выбором плотности
(x)
пропорциональной |g(x)|.
(5).
Данный метод получил название метода
существенной выборки. Замечание.
Выбрать наилучшую плотность
(x),
заданную формулой (5), на практике
часто невозможно, т.к. возможность
получить значение величину
,
как правило не выше чем значение
искомой величины а. Поэтомуна практике
ограничиваются выбором плотности
(x)
пропорциональной |g(x)|.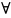 ε
> 0.
ε
> 0.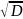 ≥
0;
≥
0;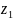 ,
… ,
,
… ,
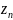 )
– случ. выборка объема n.
F0(x)
— нек. фикс-ая предполагаемая
(гипотетическая) ф-я распр-ия. Определим
простую гипотезу
)
– случ. выборка объема n.
F0(x)
— нек. фикс-ая предполагаемая
(гипотетическая) ф-я распр-ия. Определим
простую гипотезу
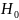 : F(x)
=
: F(x)
=
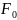 (x),
x∈R
и
сложная альтернатива общего вида H1
=
H0
. Задача проверки адекватности модели
F0(⋅)
заключается в построении критерия
для проверки H0,
H1
по выборке Z,
с наперед заданным уровнем значимости
ε∈(0,1).
Гипотеза H0
означает, что рез-ты модел-ия Z
согласуются
с распр-ем F0(⋅),
и поэтому она называется гипотезой
согласия; критерий
(решающее правило, тест) для проверки
H0,
H1
называется критерием
согласия.
(x),
x∈R
и
сложная альтернатива общего вида H1
=
H0
. Задача проверки адекватности модели
F0(⋅)
заключается в построении критерия
для проверки H0,
H1
по выборке Z,
с наперед заданным уровнем значимости
ε∈(0,1).
Гипотеза H0
означает, что рез-ты модел-ия Z
согласуются
с распр-ем F0(⋅),
и поэтому она называется гипотезой
согласия; критерий
(решающее правило, тест) для проверки
H0,
H1
называется критерием
согласия.
 -критерий
согласия Пирсона.
Пусть
вычислены частоты {
-критерий
согласия Пирсона.
Пусть
вычислены частоты { }
попадания выбор. зн-ий Z
в
ячейки гистограммы, а также соотв.
гипотетические вер-ти попадания в
ячейки, если верна H0:
}
попадания выбор. зн-ий Z
в
ячейки гистограммы, а также соотв.
гипотетические вер-ти попадания в
ячейки, если верна H0:
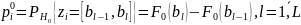
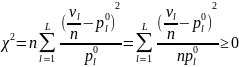 (1)
(1)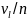 от
гипотет. зн-ий
от
гипотет. зн-ий
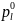 .
Чем больше
,
тем “сильнее” выборка Z
не
согласуется с H0.
.
Чем больше
,
тем “сильнее” выборка Z
не
согласуется с H0.
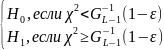
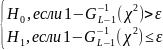
 – квантиль уровня p,
– квантиль уровня p,
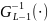 – ф-ия распр.
распр-ия
с L-1
степенями свободы
– ф-ия распр.
распр-ия
с L-1
степенями свободы
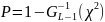 - P-значение.
- P-значение.
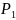 →
ε,
рекоменд. воспользоваться произволом
в выборе числа L
ячеек
и границ ячеек {bl}
таким образом, чтобы
→
ε,
рекоменд. воспользоваться произволом
в выборе числа L
ячеек
и границ ячеек {bl}
таким образом, чтобы
 ≥5
(l
=
1,
L).
≥5
(l
=
1,
L).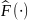 ,
а гипотетическая ф-ия распр-ия
,
а гипотетическая ф-ия распр-ия
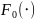 — непрерывна. Статистика
— непрерывна. Статистика
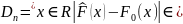 наз/
расстоянием
Колмогорова между
наз/
расстоянием
Колмогорова между
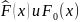 .
Отметим свойство стат.:
.
Отметим свойство стат.: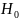 и
u
=
и
u
=
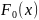 —
непр.
фун-ия, то распр-ие вер-стей стат-ки
Dn
не
зависит от конкр. вида
.
—
непр.
фун-ия, то распр-ие вер-стей стат-ки
Dn
не
зависит от конкр. вида
. не зависит от F0(⋅)
яв-ся некоторым станд. вероятностным
распр-ем, кот. можно протабулировать
для кажд. зн-ия п.
Более
того, это распр-ие при
не зависит от F0(⋅)
яв-ся некоторым станд. вероятностным
распр-ем, кот. можно протабулировать
для кажд. зн-ия п.
Более
того, это распр-ие при
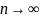 описывается распр.
Колмогорова:
описывается распр.
Колмогорова: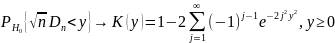 (2)
(2)
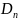 ,
имеет вид:
,
имеет вид: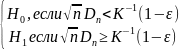
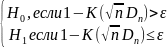
 —
квантиль
уровня 1–ε
распр.
Колм..
Асимптотический (при n
→
∞) размер
этого крит., как и крит. Пирсона, равен
ε.
—
квантиль
уровня 1–ε
распр.
Колм..
Асимптотический (при n
→
∞) размер
этого крит., как и крит. Пирсона, равен
ε.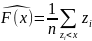 (6.3)
является строго состоятельной,
несмещенной оценкой.
(6.3)
является строго состоятельной,
несмещенной оценкой.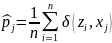 .
. ,
(6.4),
где
,
(6.4),
где
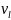 —
число выборочных значений,
попавших
в l-ю
ячейку;
I
(Δz,
z)
— индикаторная функция принимающая
значение либо 1 если z
Δz
,
либо 0 в противном случае. Гистограммой
является
статистика:
—
число выборочных значений,
попавших
в l-ю
ячейку;
I
(Δz,
z)
— индикаторная функция принимающая
значение либо 1 если z
Δz
,
либо 0 в противном случае. Гистограммой
является
статистика: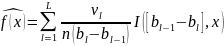
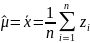
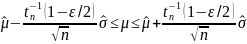
 ( p)
—
квантиль
уровня р
для
распределения Стьюдента с n
степенями
свободы.
( p)
—
квантиль
уровня р
для
распределения Стьюдента с n
степенями
свободы.