16Ряды Тейлора и Маклорена.
Определение.
Рядом Тейлора функции
в
окрестности точки
называется степенной ряд относительно
разности
,
коэффициенты которого выражаются через
и ее производные по формулам:
,
Эти коэффициенты называются коэффициентами Тейлора.
Теорема. (Условия разложимости функции в ряд Тейлора).
Если
в некоторой окрестности точки
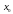абсолютные
величины всех производных функции
ограничены
одним и тем же числом
,
то функции
разлагается
в ряд Тейлора.
Другими
словами, ряд
сходится
и его сумма равна
(без
доказательства).
Определение.
Ряд Тейлора функции
в
окрестности точки
называется рядом
Маклорена:
.
Ряды
Маклорена некоторых элементарных
функций.
.
Все производные этой функции
равны
.
Функция и
ее производные ограничены в любом
интервале
значением
,
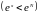следовательно, функция
разлагается
в ряд Маклорена
на всей числовой оси.
.
Тригонометрические функции.
а)
.
.
Функция и ее производные ограничены числом 1. Условия разложимости функции в ряд выполняются.
б)
.
.
Биномиальный
ряд.
Функция разлагается в ряд Маклорена в области определения (без доказательства):
Функция
Применим теорему об интегрировании рядов к ряду (16.2.1. 3. а):
Функция
Применим теорему об интегрировании рядов к ряду 16.2.1. 3. в).
Функция
Применить теорему об интегрировании рядов к ряду 16.2.1. 3.г) и записать четыре члена ряда.
Функции
и
Указание.
Возьмем ряд 16.2.1.
1. для
и заменим
на
.
Воспользуемся формулами
и
Функции
;
Ряды Фурье.Определение. Тригонометрическим рядом называется функциональный ряд
.,
членами которого являются синусы и
косинусы от целых кратных значений
аргумента
.
Числа
и
называются
коэффициентами ряда.
Некоторые
соотношения.
(
целые)
(для
любого
);
;
(для любых
и
).
Тригонометрический ряд Фурье.
Предположим, что
некоторую функцию
,
заданную на интервале
можно разложить
в сходящийся тригонометрический ряд
(см.16.3.1.),
т.е. представить в виде суммы ряда
Предполагается, что ряд (6.2.1.) можно почленно интегрировать.
Формулы для нахождения коэффициентов ряда.
.
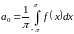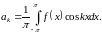
Определение. Коэффициентами Фурье функции называются числа определяемые формулами
,
.
Определение.
Ряд
называется
тригонометрическим
рядом
Достаточные условия разложимости функции в ряд Фурье.
В общем случае нельзя утверждать, что образованный выше ряд Фурье а) сходится и б) его сумма равна .
Определение.
Функция
называется
кусочно-гладкой на
интервале
,
если его можно разбить на конечное число
замкнутых
интервалов,
в каждом из которых функция
гладкая.
График кусочно-гладкой функции состоит из конечного числа гладких дуг.
Теорема. Если
функция
кусочно-гладкая на
интервале
,
то ее ряд Фурье сходится к функции
во
всех точках этого интервала, в которых
она непрерывна. В точках разрыва функции
ряд сходится к среднему арифметическому
ее предельных значений слева и справа,
т.е. к значению
,
где
точка
разрыва первого рода. (Без доказательства)
На концах интервала
сумма
ряда равна
.
Достаточные условия разложимости функции в ряд Фурье могут быть несколько другими:
Теорема. (Признак
Дирихле). Если функция
имеет на
интервале
,
конечное
число разрывов первого рода (конечных
разрывов) и конечное число экстремумов,
то ее ряд Фурье сходится к функции
во
всех точках этого интервала, в которых
она непрерывна. (Без доказательства)