1) Каждому кратному действительному корню характеристического уравнения соответствует частных решений уравнения вида

2) Каждой паре кратных комплексно сопряженных корней и характеристического уравнения соответствует частных решений уравнения вида

Лекция 13. Числовые ряды .

Линейные неоднородные дифференциальные уравнения порядка с постоянными коэффициентами (уравнения со специальной правой частью).

Отыскание частного решения уравнения со специальной правой частью

где производится по тем же правилам, что и для уравнений второго порядка (см. 12.1. ).

_{Это решение имеет вид: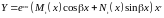} , где и некоторые многочлены степени , кратность корня в характеристическом уравнении

Определение. Пусть дана числовая последовательность Выражение называется числовым рядом, а числа членами ряда. называется общим или «энным» членом ряда.

Ряд называется заданным, если для любого натурального можно указать правило, по которому определяется соответствующий член ряда: .

Определение. Сумма первых членов ряда называется й частичной суммой ряда.

последовательность частичных сумм.

Определение. Если конечный предел последовательности частичных сумм

существует, то ряд называется сходящимся, если он не существует- то расходящимся.

Определение. Предел последовательности частичных сумм (если он существует) называется суммой ряда: .

а) сходится при , и его сумма равна ;

б) расходится при .

Если ряд сходится, то он записывается так

Свойства сходящихся рядов.

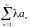Если ряд сходится и имеет сумму , то ряд сходится и имеет сумму .

Если ряды и сходятся и имеют соответственно суммы и , то ряд тоже сходится и его сумма равна .

Если ряд сходится, то ряд, полученный из данного путем приписывания или отбрасывания конечного числа членов, тоже сходится.

Определение. Разность между суммой сходящегося ряда и его частичной суммой называется м остатком ряда.

Остаток ряда это сумма бесконечного ряда (его сходимость вытекает из свойства 13.2.2.3. сходящихся рядов) .

Теорема (Необходимый признак сходимости числового ряда). Если числовой ряд сходится, предел (при ) общего члена ряда равен 0.

Доказательство. .

Если ряд сходится, то и .

Следствие. (Достаточный признак расходимости числового ряда). Если предел (при ) общего члена ряда не равен 0, то ряд расходится.

Лекция 14. Числовые ряды .

Достаточные признаки сходимости.

Лемма. Если частичные суммы ряда с положительными членами ограничены сверху:

, то ряд сходится.

Признаки сравнения. Теорема. Пусть даны два ряда с положительными членами:

и ,

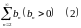и пусть, для любого номера выполняется условие .

Тогда:

а) Если ряд сходится, то ряд сходится.

б) Если ряд расходится, то ряд расходится.

Признак сравнения в предельной форме.

Если 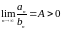, то ряды и одновременно оба сходятся или оба расходятся.

Признак Даламбера. Пусть дан ряд с положительными членами и существует конечный или бесконечный (предел отношения последующего члена ряда к предыдущему), то если 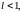то ряд сходится, если то ряд расходится.

Радикальный признак Коши. Теорема. Пусть дан ряд с положительными членами и существует конечный или бесконечный , то если то ряд сходится, если то ряд расходится. (Без доказательства)

Интегральный признак Коши. Теорема. Пусть дан ряд члены которого являются значениями положительной непрерывной функции при целых положительных значениях аргумента

и пусть монотонно убывает в интервале .

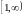Тогда:

а) если сходится несобственный интеграл , то ряд сходится,

Гармонический ряд. Определение. Ряд называется гармоническим.Гармонический ряд расходится.

Сходимость рядов .

Знакочередующиеся ряды. Определение. Ряд вида называется знакочередующимся.

Теорема Лейбница. Если в знакочередующемся ряду абсолютные величины членов ряда убывают , и общий член стремится к нулю , то ряд сходится. Сумма ряда по абсолютной величине не превышает абсолютной величины первого члена ряда.

Следствие. Остаток ряда (см. 13.2.2.4. Определение.), удовлетворяющего теореме Лейбница, не превышает по абсолютной величине модуля первого отбрасываемого члена. .

Действительно, остаток ряда представляет собой ряд, удовлетворяющий теореме Лейбница, и, поэтому его сумма не превышает по модулю .

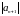Ряды с произвольным распределением знаков.

Теорема. Пусть дан ряд с произвольным распределением знаков. Если ряд, составленный их абсолютных величин членов данного ряда, сходится, то и данный ряд сходится.

Определение. Ряд, абсолютные величины членов которого образуют сходящийся ряд, называется абсолютно сходящимся.

Определение. Если ряд сходится, а абсолютные величины его членов образуют расходящийся ряд, то он называется условно сходящимся.

Лекция 15. Функциональные ряды..

Определение. Ряды, членами которых являются функции, называются функциональными рядами:

Предполагается, что все функции определены и непрерывны на одном и том же интервале, конечном или бесконечном.

Определение. Точка называется точкой сходимости ряда, если числовой ряд сходится.

Множество всех точек сходимости называется областью сходимости ряда.

Определение. Точка называется точкой абсолютной сходимости ряда, если числовой ряд сходится абсолютно (см. 14.2.2.2. Определение.)

Определение. Функциональный ряд называется мажорируемым рядом в области , если в этой области все его члены не превосходят по абсолютной величине членов некоторого числового сходящегося ряда с положительными членами.

То есть, в области выполняется неравенство: , где член сходящегося числового ряда , который называется мажорантой или мажорирующим (усиливающим) по отношению к данному ряду.

Теорема. Если функциональный ряд мажорируемый в области , то во всех точках этой области он сходится абсолютно.

Свойства мажорируемых рядов.

Теорема 1. Если ряд из непрерывных функций мажорируемый в области ,то его сумма является непрерывной функцией в этой области.

Теорема 2. Если ряд, составленный из непрерывных функций, мажорируемый в области , то интеграл от суммы ряда в этой области равен сумме ряда, составленного из интегралов этих функций.

.

Мажорируемый ряд можно почленно интегрировать.

Теорема 3. Пусть ряд , составленный из функций, имеющих непрерывные производные в области , имеет сумму , а ряд, состоящий из производных этих функций 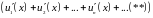, является мажорируемым в этой области.

Тогда сумма ряда 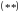, состоящего из производных, равна . .

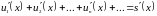Если ряд, составленный из производных членов заданного ряда, мажорируемый, то заданный ряд можно почленно дифференцировать.

Равномерно сходящиеся ряды.

Определение. Функциональный ряд называется равномерно сходящимся в области если для любого 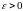существует такое (не зависящее от ), что для всех выполняется неравенство .

Всякий, мажорируемый в области ряд является равномерно сходящимся в этой области(без доказательства). Теоремы 1-3 верны для равномерно сходящихся рядов.

Определение. Степенным рядом называется функциональный ряд , где коэффициенты степенного ряда.

В частности при , ряд будет иметь вид: .

Теорема Абеля. Если степенной ряд 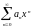сходится в точке , то он сходится абсолютно во всех точках интервала , то есть при любом , удовлетворяющем неравенству .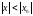

0

Следствие. Если степенной ряд расходится в точке , то он расходится при любом , удовлетворяющем неравенству , то есть во всех точках интервала .

Область сходимости степенного ряда . Возможны три случая:

1) Область сходимости состоит из одной точки . Пример. Ряд 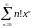расходится при всех , кроме , так как общий член ряда не стремится к нулю при любом .

2) Область сходимости состоит всех точек числовой оси.

Пример. Ряд сходится при всех . 3) Область сходимости состоит более чем из одной точки числовой оси, причем на оси есть также точки, в которых ряд расходится. Определение. Радиусом сходимости степенного ряда называется положительное число такое, что при ряд сходится, а при 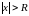ряд расходится. Интервал называется областью сходимости.

Нахождение радиуса сходимости степенного ряда и Радиус сходимости степенного ряда можно находить по формулам

и .

Свойства степенных рядов.

Лемма1. Степенной ряд является мажорируемым в любом интервале , целиком лежащем внутри интервала сходимости .

Лемма 2. Ряд , составленный из производных членов степенного ряда имеет тот же радиус сходимости, что и ряд .

Свойства степенных рядов:

Сумма степенного ряда есть функция, непрерывная в интервале сходимости.

.

Степенной ряд можно почленно интегрировать и дифференцировать в интервале сходимости любое число раз.

а)

б)

Получившиеся ряды имеют тот же радиус сходимости, что и данный.