1. Динамический анализ

НПФ: Неявная параметрическая форма

y920 =x1920&x2920

ЯПФ: Явная параметрическая форма

y920(t) =x1920(t) &x2920(t)

Подготовка и испытание схемы

ВД: Временная диаграмма ЛС: Логическая схема

Соотношение времен переднего и заднего фронтов

ty(0-1) =max(tx1(0-1),tx2(0-1) – по более позднему 01-переходу

ty(1-0) =min(tx1(0-1),tx2(0-1) – по более раннему 10-переходу

3. Дизъюнктор (Или, Or)

1. Исходные построения

СФО: Структурная формула объекта

y920 = V(x1920, x2920) = (x1920 V x2920) = (x1920, x2920)V

Варианты записи:

y920 =x1920x2920

ЛИ: Логическая интерпретация

y920 равноx1920 илиx2920

y920equalx1920orx2920

ССО: Структурная схема объекта

построение ССО методом мозаичного набора:

ЛС: Логическая схема системы анализа

Функциональные соотношения

(по номерам комбинациям состояний входов)

0: x1920 = 0 x2920 = 0 y920 = 0

1: x1920 = 0 x2920 = 1 y920 = 1

2: x1920 = 1 x2920 = 0 y920 = 1

3:x1920 = 1x2920 = 1y920 = 1

ФТО: Функциональная таблица объекта – таблица истинности

Форма 1

№	x1920	x2920	y920
0 1 2 3	0 0 1 1	0 1 0 1	0 1 1 1

Форма 2 // Аналог таблицы Карно

&	0	1
0	0	1
1	1	1

ФГО: Функциональный график объекта

ФВ: Функциональное выражение

O:y920 =Max(x1920,x2920) = ((x1920+x2920)+|x1920–x2920|)/2

2. Динамический анализ

НПФ: Неявная параметрическая форма

y920 = x1920 V x2920

ЯПФ: Явная параметрическая форма

y920 (t) = x1920 (t) V x2920 (t)

Подготовка и испытание схемы

Соотношение времен переднего и заднего фронтов

ty(0-1) =min(tx1(0-1),tx2(0-1) – по более раннему 01-переходу

ty(1-0) =max(tx1(0-1),tx2(0-1) – по более позднему 10-переходу

4. Дополнительные многополюсные элементы

1. Инверсный конъюнктор и дизъюнктор

1. Элемент Не-И (NotAnd:nand)

СФО: Структурная формула объекта (и правила де Моргана)

y920=N(x1920&x2920) =Nx1920VNx2920

ЛИ: Логическая интерпретация

y920 равно Не (x1920 иx2920)

y920 equal Not (x1920 and x2920)

ССО: Структурная схема объекта

БСО: Блок-схема объекта ШСО: Штрих-схема объекта

построение ССО методом мозаичного набора:

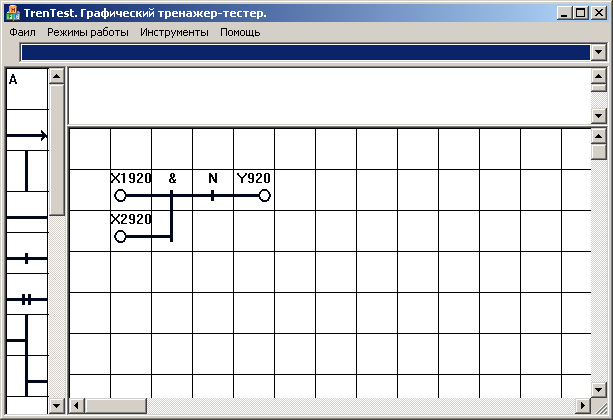
2. Элемент Не-Или (NotOr:nor)

СФО: Структурная формула объекта (и правила де Моргана)

y920=N(x1920Vx2920) =Nx1920&Nx2920

ЛИ: Логическая интерпретация

y920 равно Не (x1920 илиx2920)

y920 equal Not (x1920 or x2920)

ССО: Структурная схема объекта

БСО: Блок-схема объекта ШСО: Штрих-схема объекта

построение ССО методом мозаичного набора:

Дистрибутивность

1) Выполняется левая антидистрибутивность инверсии

относительно конъюнкции и дизъюнкции – правила де Моргана:

// левая – для прямой функциональной записи

// правая – для прямой схемной записи

y920 = N(x1920 & x2920) = Nx1920 V Nx2920

y920 = N(x1920 V x2920) = Nx1920 & Nx2920

построение ССО методом мозаичного набора:

2. Сумма по модулю (разделительная дизъюнкция)

y920 = x1920  x2920 = (x1920 & Nx2920) V (x2920 & Nx1920) = x1920x2920' V x2920x1920'

построение ССО методом мозаичного набора: