
- •1.Предмет, цели и задачи эконометрики (э). Экон.Модель (эм), основные этапы построения экон.Модели.
- •2.Простая линейная регрессия. Классические предположения модели.
- •3.Стат.Оценивание парам плр по мнк. Св-ва оценок.
- •4.Проверка качества плр: значимость параметров, адекватность моделей. Прогнозирование.
- •5.Множественная линейная регрессия (млр). Классич. Предположения. Мнк-оценка параметров модели.
- •6.Свойства мнк-оценок млр. Теорема Гаусса-Маркова.
- •7. Проверка качества множественной линейной регрессии: значимость параметров, доверительные интервалы, адекватность модели. Прогнозирование.
- •8.Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
- •9.Спецификация экономической модели: выбор формы зависимости нелинейной модели.
- •10. Проблема гетероскедастичности модели. Критерии её диагностики.
- •11.Взвешенный мнк в задаче оценивания параметров модели. Свойства оценок взвешенного мнк.
- •12.Проблема автокорреляции остатков модели. Последствия автокорреляции при использовании модели.
- •13. Критерий диагностики автокорреляции Дарбина-Уотсона.
- •14. Методы устранения автокорреляции
- •15. Проблема наличия мультиколлинеарности модели. Последствия наличия и диагностика мультиколлинеарности.
- •16. Методы устранения мультиколлинеарности.
- •17. Динамические модели с распределёнными лагами.
- •18. Структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)
- •19. Понятие временного ряда(вр). Модель вр, основные задачи анализа вр. Методы сглаживания вр (скользящего среднего, экспоненциального сглаживания, последовательных разностей)
- •20. Стационарность вр. Характеристики корреляции уровней вр.
- •21. Стационарные модели временных рядов: авторегрессии, скользящего среднего арсс.
- •22. Системы одновременных эконометрических уравнений (соу). Структурная и приведенная форма соу (графическое и матричное представление)
- •23. Проблемы идентификации соу. Идентифицируемость уравнений соу.
- •24. Методы оценивания соу. Косвенный мнк. Двухшаговый мнк. Применимость и свойства оценок.
- •25. Современное состояние эконометрики. Примеры больших эконометрических моделей.
4.Проверка качества плр: значимость параметров, адекватность моделей. Прогнозирование.
Кроме задачи оценивания параметров представляет интерес задача о значимости параметров, т.е. задача проверки отделимости параметров регрессии от нуля, которая решается проверкой статистических гипотез при выполнении классических предположений П1-П5:
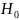 (
):
=0;
где t(
)
=
(
):
=0;
где t(
)
=
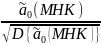 ;
;
(
):
=0;
где t(
)
=
 .
.
Решающее правило для проверки гипотез:
Если |t( )|> , где - квантиль распределения Стьюдента с надёжностью γ, то отклоняют гипотезу и делают вывод о существенной значимости параметра . Аналогично для .
Вторая задача проверки качества модели основана на адекватности (обоснованность выбора принятой в соответствии с моделью регрессии взаимосвязи у и х). Мера адекватности – коэф. детерминации:
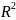 =
=
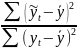 =
=
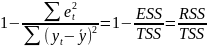 ,
гдеTSS
– вся D,
ESS – необъясненная часть D, RSS
- объяснен. TSS=
ESS+RSS
,
гдеTSS
– вся D,
ESS – необъясненная часть D, RSS
- объяснен. TSS=
ESS+RSS
Часто
используется скорректированныйкоэф.детерм.
(с учётом степеней свободы):
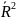 =
=
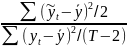 .
.
Решающее
правило: Если
(T-2)/((1-
)/2)
>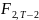 (γ),
то отвергается гипотезе о неадекватности
ПЛР (
(γ)
– квантиль порядка γ закона распределения
Фишера).
(γ),
то отвергается гипотезе о неадекватности
ПЛР (
(γ)
– квантиль порядка γ закона распределения
Фишера).
Если
= 1, то ПЛР полностью отражает зависимость
у от х. Все наблюдаемые точки
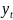 лежат на графике
=
+
лежат на графике
=
+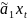 .Если
= 0, то модель неадекватна и информация
о х не влияет на изменения у.
.Если
= 0, то модель неадекватна и информация
о х не влияет на изменения у.
Нельзя придавать большое значение коэф-ту детерминации, надо дополнять проверку адекватности другими показателями; для ПЛР совпадает спарным коэф-том корреляции.
По модели ПЛР можно построить прогноз зависимой переменной уна горизонт будущего:
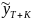 =
+
=
+
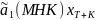 ,
где K
– глубина прогноза в будущем,
,
где K
– глубина прогноза в будущем,
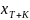 - планируемое в будущем моменте времени
T+K значение факторной переменной. Чем
дальше глубина прогноза, тем менее
чётким он будет.Доверительный интервал
прогноза:
- планируемое в будущем моменте времени
T+K значение факторной переменной. Чем
дальше глубина прогноза, тем менее
чётким он будет.Доверительный интервал
прогноза:
-
S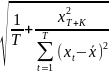 <
<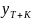 <
+
S
.
<
+
S
.
5.Множественная линейная регрессия (млр). Классич. Предположения. Мнк-оценка параметров модели.
y
= f(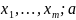 )+ε,
где описывается зависимость одной
эндогенной переменной от m (m>1) экзогенных
переменных.
)+ε,
где описывается зависимость одной
эндогенной переменной от m (m>1) экзогенных
переменных.
y
=
+
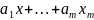 + ε.
+ ε.
Используют
векторно-матричное представление
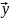 = X
= X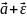 .
.
X = 1
= 1
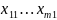 ,
=(
,
=(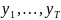 )’,
)’,
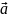 =(
=(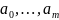 )’,
)’,
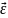 =(
=(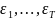 )’,
)’,
::::::::: :::::::
1
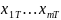
По степени владения априорной информацией различ. 2 задачи:
1)при неизвестной функции взаимосвязи – задача подбора структуры модели.
2)при заданной функции – задача оценивания неизвестных параметров. Основной метод оценивания параметров - метод наименьших квадратов (минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от её значения, рассчитанного по модели), кот.обеспечивает оптимальные свойства оценкам только при выполнении классических предположений:
П1.
отсутствие систематич.ошибок наблюдений
уравнения регрессии: M{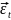 }
=
}
=
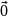 ,
t=1,…,T.
,
t=1,…,T.
П2.
случайные ошибки некоррелированы между
собой: M{εε'}=0.Коэфф
корреляции:
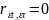 .
.
П3. наблюдения производятся с одинаковой точностью, т.е. дисперсии случ. переменных одинаковы во все моменты измерения: D{ } = , t=1,…,T.
П4.
Экз.переменные измеряются без ошибок.
В случае модели МЛР их значения образуют
линейно-независимые векторы. det(X’X)
0
=>rank(X)
= min(T,
m+1).
Отсутствие мультикол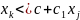
П5.
Ошибки
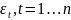 имеют
нормальное совместное распределение
имеют
нормальное совместное распределение N(0,
).
N(0,
).
МНК-оценки
находятся как решение задачи Q(
)
= (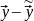 )’
* (
)
→min
– квадратическая форма (где
)’
* (
)
→min
– квадратическая форма (где
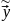 = Х
= Х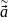 ,
- вектор оценок множества неизвестных
параметров
)
и имеют вид
(МНК)
=
,
- вектор оценок множества неизвестных
параметров
)
и имеют вид
(МНК)
=
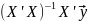 - матричная форма.
- матричная форма.
