Проектирование сетей эвм.

Теория проектирования сетей ЭВМ базируется на аппарате систем массового обслуживания(СМО).

Обозначим n-e требование, поступающее в СМО через

- момент поступления требования

- время между соседними требованиями и .

- среднее время между соседними требованиями

- среднее время обслуживания.

Для обозначения различных типов СМО используется обозначение, которое имеет вид A/B/m. Так обозначается СМО с m обслуживающими приборами, а A и B указывают соответственно на распределение времени между соседними требованиями и распределение времени обслуживания. А и В принимают значение из следующего набора символов:

M – показательное распределение (Markovian), - распределение Эрланга порядка r.

- гиперпоказательное распределение порядка r, D- постоянная величина(Deterministic),

G – произвольное распределение (General).

Наиболее важным параметром СМО G/G/1 является коэффициент использования

,

где - плотность входного потока (средняя скорость поступления требований в систему),

- плотность потока обслуживания.

Эта величина равна доле времени, в течении которого занят единственный обслуживающий прибор, и она также равна отношению требуемой от данной системы скорости обслуживания к пропускной способности системы ( ).

Для многолинейной СМО G/G/m

Интерпретируется как математическое ожидание доли занятых приборов, если любой прибор имеет одно и то же распределение времени обслуживания.

В общем случае - математическое ожидание доли используемой пропускной способности системы. В любой стабильной системе

Случай не допускается. Чем ближе к 1, тем больше очереди и время ожидания.

Среднее время пребывания требования в системе:

- среднее время ожидания в очереди.

Среднее число требований в очереди:

- формула Литтла.

Соответствующий результат для числа требований в очереди:

- средняя длина очереди.

Для системы G/G/m справедливо:

(следует из формулы Литтла ).

₍₁₎

Для системы M/M/1 вероятность того, что в системе находится k требований равна

;

Отсюда среднее число требований в системе:

,

а дисперсия равна:

.

Используя формулу Литтла и (1) при m=1 получим две основные характеристики М/M/1 – ее средние характеристики:

;

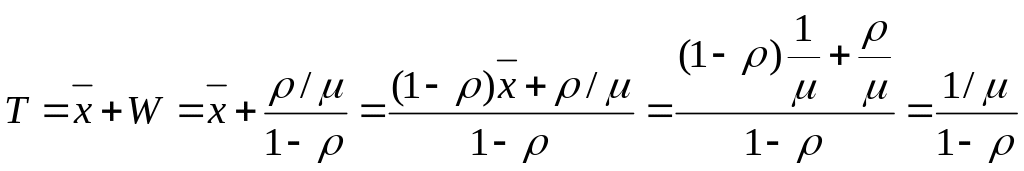(2)

Величины , , растут по мере убывания (1- ). При средние задержки и длины очередей растут неограниченно.

Пусть сеть с коммутацией сообщений имеет М каналов и N узлов. Каналы – бесшумные и абсолютно надежные. Пропускная способность i-го канала равна (бит в секунду). Поток, поступающий в сеть из внешних источников(например, из машины HOST )образует Пуассоновский процесс со средним значением (сообщений в секунду) для тех сообщений, которые возникают в узле j и предназначены для узла k.

Полный внешний поток, поступающий в сеть, равен:

.

Длины всех сообщений по предположению независимы и распределены по экспоненциальному закону со средним значением 1/ (бит) (пока не учитывается возможная пакетная структура сообщений).

Для высокоскоростных сетей, покрывающих большие географические расстояния, может оказаться важным включить в рассмотрение время распространения бита через i-ый канал ( *скорость света) , таким образом если сообщение имеет длину в битах, то время, в течение которого оно занимает канал, равно секунд.

Заметим, что случайность временного обслуживания появляется не из-за обслуживающего прибора(канала), а из-за требования (сообщения), так как длина сообщения является случайной величиной.

Поскольку любой канал в сети рассматривается как отдельный обслуживающий прибор, обозначим через среднее число сообщений в секунду, проходящих через i-ый канал.

Как и для внешнего потока, определим полный поток в сети:

.

Предположим, что стоимость построения i-го канала с пропускной способностью задается некоторой произвольной функцией .

Пусть - стоимость всей сети (по предположению состоит лишь из стоимости каналов):

.

Выше была определена задержка сообщения как такое время, которое сообщение проводит в сети.

Средняя задержка сообщения в сети - главная характеристика сети.

[задержка сообщения]

Обозначим

[задержка сообщения, которое возникло в j и имеет место назначения k].

Ясно, что

(3)

так как доля полного входящего потока имеет в среднем задержку, равную .

Последнее равенство представляет разложение сети по параметрам источник – адресат.

При построении сетей возникает множество задач, и к основным из них относятся следующие задачи:

1. выбор пропускной способности каналов { };

2. выбор потоков в каналах { };

3. выбор топологии.

Считается, что на стоимость сети накладываются ограничения.

Определим 4 задачи, которые отличаются только множеством переменных, варьируемых при проектировании. В каждой из этих задач считается, что заданы положения узлов, внешний поток , стоимость каналов , постоянные D и , а так же предполагается, что используемые потоки { } являются реализуемыми (то есть они согласуются с пропускной способностью и ограничениями на внешний поток, а также удовлетворяют закону сохранения).Первая задача – это выбор пропускных способностей (ВПС).

Задача ВПС.

Дано:	потоки { } и топология сети.
Минимизировать:	.
Варьируются:	{ }.
Ограничение:	.

Вторая задача – распределение потоков(РП).

Задача РП

Дано:	Пропускные способности { } и топология сети.
Минимизировать:	.
Варьируются:	{ }.

Третья задача – задача выбора пропускных способностей и распределения потоков(ВПС и РП).

Задача ВПС и РП.

Дано:	топология сети.
Минимизировать:	.
Варьируются:	{ }и { }.
Ограничение:	.

Четвертая задача – задача выбора топологии, пропускных способностей и распределения потоков (ВТ, ПС и РП)

Задача ВТ, ПС и РП.

Минимизировать:	.
Варьируются:	топология, { }и { }.
Ограничение:	.

Эти 4 задачи в настоящее время решены с различной степенью полноты.

Обозначим через путь, по которому идут сообщения, возникшие в узле j, к узлу назначения k. i-ый канал (с пропускной способностью ) включен в путь , если сообщения, идущие по этому пути, проходят указанный канал ( ). Тогда средняя интенсивность потока сообщений в i-м канале равна сумме средних интенсивностей потоков по всем путям, которые проходят через этот канал, то есть

(4)

Заметим, что представляет собой сумму средних задержек, испытываемых сообщениями при передаче по различным каналам пути .

[время, затраченное на ожидание и процесс передачи по i-му каналу],

то есть - среднее время, проведенное сообщением в системе, где под системой понимается i-ый канал:

₍₅₎

Отсюда из (3) получаем:

₍₆₎

Изменим порядок суммирования, тогда как обычно при изменении порядка суммирования условие на i становится условием на j,k. В результате имеем:

Используя соотношение (4), получаем:

(7)

Теперь средняя задержка сообщения разложена на компоненты , относящиеся к отдельным каналам, то есть разложена по .

Предположение о независимости. Всякий раз, когда сообщение принимается в узле внутри сети, независимо с плотностью распределения

выбирается его новая длина .

Это предположение показано с помощью многочисленных моделирований для реальных сетей. Это утверждение, вообще-то говоря, неверно, так как сообщения сохраняют длину при их прохождении по сети, но как показано, влияние этого предположения на пренебрежимо мало в большинстве сетей.

Пользуясь этим предположением, получим, что i-ый канал теперь можно рассматривать как систему М/М/1 с пуассоновским потоком интенсивности на входе и показательным временем обслуживания со средним 1/ секунд. Решение сразу же получаем из (2).

.

И поэтому, согласно (5), имеем¹:

(8)

Анализ (4) показывает, что при увеличении нагрузки на сеть никакое слагаемое в выражении (4) не будет доминировать, пока поток в одном из каналов (например, в ) не достигнет пропускной способности этого канала по соответствующему узкому месту сети.

В этой точке , и следовательно быстро растут, то есть имеется порог по .

Это пороговое поведение задержки показано(упрощено) на рис. 9.

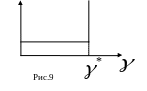
определяется как задержка в отсутствии нагрузки (незагруженная сеть).

Из (4) при и получим:

.

- нагрузка насыщения, при которой .

Определим как длину пути , где над длиной понимается число каналов в пути. Средняя длина пути выражается как

.

Рассмотрим полный поток в сети . Отметим, что вклад потока j-k в полный поток равен , так как сообщений пройдут участков при движении по сети.

Следовательно:

.

Из последних двух равенств получаем известный общий результат:

.

Отсюда .

Это дает метод вычисления задержки в отсутствии нагрузки для упрощенной пороговой модели.

Отыскание нагрузки насыщения выполняется непосредственно. Она соответствует наименьшему значению , при котором . Поэтому при заданной фиксированной процедуре выбора маршрутов можно просто найти многие { } с помощью формулы

при любом . После этого нужно посмотреть все отношения и определить на наибольшем из этих отношений. Далее все потоки уменьшаем на масштабируемый коэффициент, при котором . Значение при котором это равенство будет иметь место равно .

Весьма важно отыскание максимального потока, который сеть может переносить между данной парой углов. Это можно выполнить с помощью хорошо известной теоремы о максимальном потоке и минимальном сечении. Согласно этой теореме, максимальный поток, который сеть может переносить между некоторым источником (узлом) s и адресатом (узлом) t, равен величине минимального сечения s-t.

Любая совокупность ребер, при устранении которой из сети прерывается весь поток от источника s к адресату t, называется сечением s-t.

Пропускная способность сечения представляет собой полный поток, который устраненные ребра может переносить от источника s к адресату t.

Минимальным сечением s-t называется сечение, которое имеет наименьшую пропускную способность. Существуют алгоритмы нахождения максимального потока между данным источником и адресатом.

Контрольные вопросы:

1. Дайте определение коэффициента использования?

2. Чему равно среднее время пребывания для системы M/M/1? Какая величина называется стоимостью сети?

3. Дайте определение средней задержки в сети. Приведите итоговую формулу.

4. Сформулируйте задачи ВПС, РП, ВПС и РП.

5. Чему равна средняя задержка в канале?

6. Чему равна средняя длина пути в сети?

7. Чему равно среднее время ожидания в очереди для системы M/M/1?

8. Чему равен максимальный поток, который сеть может переносить между некоторым источником и адресатом?

Лекция 4.