4.3.1 Аппроксимация функций

Определение. Аппроксимацией 1-го порядка или линейной аппроксимацией функции класса в окрестности некоторой точки называют линейную функцию

(2)

Для в малой окрестности величина ~ .

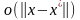Определение. Аппроксимацией 2-го порядка или квадратной аппроксимацией функции класса в окрестности некоторой точки называют функцию

(3) функция будет квадратичной функцией по и справедлива оценка ~ .

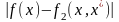Эти аппроксимации основаны на разложении в ряд Тейлора функции . В оптимизации могут использоваться и другие виды аппроксимаций: если – периодическая функция или близка к ней, то её можно аппроксимировать кусками рядов Фурье.

2. Общая схема методов 1-го порядка

На первой итерации решается задача , где – окрестность точки некоторой формы с размерами .

Решение этой задачи принимается за , переходим ко второй итерации и т.д., на -ой итерации в методах первого порядка по известному решается задача:

(4)

где – некоторая окрестность точки размерами , решение принимается за и т. д.

Таким образом, методы 1-го порядка для задачи (1) отличаются лишь выбором формы и размером окрестности.

Индекс у означает, что на практике на различных итерациях окрестность может выбираться по-разному.

Примеры окрестностей:

1) – шар в с центром в и радиусом .

2) – куб в с центром в размером .

Существуют способы задания окрестностей, которые могут учитывать топологию функции .

. Геометрическая интерпретация.

Дана функция , дана точка , тогда задаём окрестность , в ней функция заменяется касательной , min её – , затем берём и т. д.

4.3.3 Выбор направления и шага в методах 1-гопорядка. Градиентные методы

Задачу (4) будем решать в 2 этапа:

I этап: построение направлений итерации. Полагаем в задаче (4) по известному : где , в результате приходим к задаче:

(5)

где – некоторая окрестность начала координат в размерами . В результате решения задачи (5) получаем некоторый вектор . Он выбирается за направление на -ой итерации. При выборе направления его размеры не важны, поэтому , то есть имеет единичную длину.

Константа в (5) также на направление не влияет и её отбрасывают. Таким образом, для нахождения решается задача:

(5*)

Пример. Рассмотрим в (5) случай, когда окрестность есть единичный шар, то есть будем решать задачу:

(6)

Решаем задачу (6) геометрически: .

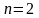– оптимальный план задачи (6).

Поскольку размеры направления нас не интересуют, то в методах 1-го порядка используют направление

– направление антиградиента (7)

Методы 1-го порядка с таким направлением называются градиентными. Градиентные методы – наиболее популярные методы 1-го порядка. Если выбрать подходящий шаг, то они всегда позволяют уменьшить целевую функцию. Однако существуют задачи (1) с так называемой «овражной структурой», для которых градиентные методы плохо сходятся и надо направление выбирать другим (по-другому выбирать окрестность ).

Геометрическая интерпретация «овражной структуры».

– линия с постоянной высотой над уровнем океана. В случае «овражной структуры», как правило, градиент имеет большую длину и направлен почти перпендикулярно к направлению ведущему к оптимальному плану.

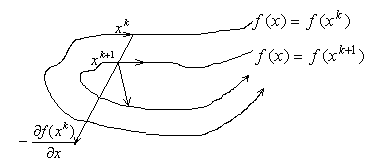
Замечание. В случае «овражной структуры» надо строить с учётом линий уровня целевой функции, желательно знать кривизну, 2-ую производную.

II этап: решение задачи (4), когда по известному приближению построено направление выбирается размер окрестности , то есть определяется размер шага в этом направлении.

Наиболее распространены 3 способа:

а) наилучший шаг в заданном направлении, решается задача

(8)

где . Точное решение задачи (8) выбирается за .

Определение. Метод 1-го порядка, в котором шаг выбирается в виде (7), а направление наилучшим называется методом наискорейшего спуска.

б) , где – малое число, при этом способе на всех итерациях шаг выбирается одинаковым.

Замечание. Если шаг выбрать достаточно большим, то даже если направление позволяет уменьшить целевую функцию, с этим шагом функция возрастёт. (Перейдём на противоположную сторону оврага и более высокую.)

в) метод последовательного дробления.

При таком выборе шага задача (8) решается подбором. Выбираем сначала и сравниваем значения и . Если между числами знак , то шаг большой (целевая функция увеличивается) и уменьшают в несколько раз (10). Поле чего повторяем сравнение. Если знак , то шаг подходит, но и в этом случае его можно улучшить (в несколько раз увеличить или уменьшить ). Существуют специальные схемы подбора шага итераций.