Необходимое условие.

II НЛП, ВП.

1. Исследование задач на безусловный минимум (с док.) Схема исследования.

2. Принцип Лагранжа + схема лаб.раб.№2 (часть 2)

III Вычислительные методы

1. Метод ветвей и границ (общая схема)+лаб.раб.№3 (часть 2)

2. Методы безусловной минимизации(градиент, наискорейшего спуска, Ньютон,…) +лаб.раб.№4 (часть 2)

IV Варианты исчисления

1. ОЗВИ ОМ

Вариации h, вариация ∂I(ξ,h)

Необходимые условия оптимальности в терминах вариации.

2. Условие Эйлера, его применение +лаб.раб.№6 (часть 2)

Достаточное условие: поговорить.

В вопросе:

1. Постановка задачи.

2. Содержание вопроса.

3. Применение на практике.

Ответы

II

1. Исследование задач на безусловный минимум (с док.) Схема исследования.

Глава III нелинейное программирование

Здесь рассматривается задача , (1)

в которой функция в общем случае является ни линейной, ни выпуклой, а при формировании множества 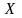могут участвовать нелинейные ограничения. Справедливо включение ЛП ВП НЛП.

Классификация

Задача (1) имеет общую форму, и если не накладывать дополнительные условия на функцию и множество , то содержательных результатов не удается получить. Поэтому задачу (1) разбивают на специальные классы задач, используя аналитическое свойство функции (гладкость) и форму ограничений (уравнений и неравенств).

1. Задача на безусловный минимум

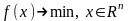
На множество планов не накладывается никаких ограничений, отсюда и название класса. Предполагается или .

Задача имеет вид: (1)

то есть .

3.1.1. Условие оптимальности

Теорема 1. Если – локально-оптимальный план, то (2)

Теорема 2 (Необходимое условие оптимальности второго порядка). Если – локально-оптимальный план, то (3)

Определение. Точка называется стационарной точкой функции , если она является решением системы (4)

(4)

Теорема 3 (Достаточное условие оптимальности). Если – стационарная точка функции и , (5) то – локально-оптимальный план (1) (по крайней мере).

Доказательство. Доказательство теорем 1-3 основано на разложении функции ( переменных) в ряд в окрестности точки (см. главу 2).

Ч.т.д.

Замечание. При проверке условий (3) и (5) применяются критерии Сильвестра неотрицательности и положительности квадратных матриц.

3.1.2 Схема исследования задач типа (1)

1) Проверяем условие существования решения задачи (1), при этом применяется критерий существования решения . В общем случае, при , вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.

2) Составляем систему (4) и находим стационарные точки функции (все). Только среди них может находиться оптимальный план и все локально-оптимальные планы. Пусть – все стационарные точки функции .

3) Для каждой стационарной точки проверяем выполнение или невыполнение условий (3)-(5). Пусть – стационарная точка, тогда возможны случаи:

а) . Тогда, согласно теореме 3 – локально-оптимальный план.

б) . Тогда для нее выполняются условия теоремы 2, но не выполняются условия теоремы 3. Тем не менее, она остается подозрительной на решение задачи (1) (то есть она может оказаться и оптимальным планом и локально-оптимальным планом).

в) Не выполняется ни а) ни б). Тогда эту точку исключают из дальнейшего рассмотрения.

4) Делаем окончательный вывод: среди точек, оказавшихся либо локально-оптимальными планами, либо подозрительных на решение, находим лучшую, то есть подставляем точки в целевую функцию и лучшей будет точка с наименьшим значением функции. Если доказано существование решения и построены все стационарные точки, то лучшая точка будет оптимальным планом. В общем случае, из-за сложности функции и невозможности найти все решения системы (4) исследование нельзя провести полностью и лучшая точка остается подозрительной на решение задачи.

2. Принцип Лагранжа + схема лаб.раб.№2 (часть 2)

Пусть дана задача: (1)

Теорема 1 (Обобщённое правило множителей Лагранжа). Если – локально-оптимальный план задачи (1), то необходимо найдётся такой обобщённый вектор Лагранжа , что

Определение. Некоторый план задачи (1) (здесь необязательно оптимальный) будем называть обыкновенным, если вектора

(7)

линейно независимы .

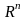Теорема 2 (Классическое правило множителей Лагранжа). Если – обыкновенный локально-оптимальный план задачи (1), то всегда найдётся такой единственный классический вектор Лагранжа , что выполняется условие: