Основные понятия и аксиомы статики.

Статика – раздел теоретической мех., изучающий законы сложения (разложения) сил и условия равновесий тел под действием сил. Абсолютно твердое тело – тело, расстояние между любыми точками которого всегда постоянно. Материальная точка – тело, размерами которого можно пренебречь в данной задаче по сравнению с размерами -др. тел или расстояниями м/д телами. Сила – мера взаимодействия тел, векторная величина, характеризуется 3-мя независимыми параметрами: 1. Точка приложения силы. 2. Направление или линия действия. 3. Модуль или величина. Система сил – совокупность сил, действующих на данное тело или на данную систему сил 2 системы называется эквивалентными, если оказывают одинаковое мех. воздействие на тело . Уравновешенная система сил – если при ее действие на тело оно находится в равновесии . Равнодействующей называется сила, эквивалентная данной системе сил (не всякая система сил имеет равнодействующую.). Все силы делятся на внешние – которые действуют на данное тело (систему сил) со стороны др. тел и внутренние - силы взаимодействия между частями тела.

1 аксиома: для того, чтобы тело находилось в равновесии под действием двух сил, эти силы должны быть равны по модулю и направлены по одной прямой в противоположные стороны.

2 аксиома: не изменяя кинематического состояния тела к силам, действующим на него всегда можно добавить, или отнять уравновешенную систему сил. Следствие из 2-ой аксиомы: в твердом теле точку приложения силы всегда можно переносить по ее линии действия, т.е. сила является скользящим вектором.

_{3 аксиома}. Закон равенства и противодействия: два тела действуют друг на друга с силами, равными по модулю и противоположно направленными по одной прямой

4 аксиома. Закон сложения сил – правило параллелограмма: две силы, приложенные в одной точке тела имеют равнодействующую, приложенную в этой же точке, а по величине и направлению эта равнодействующая задается диагональю параллелограмма, построенного на исходных силах. , .

5 аксиома. Принцип отвердевания: если тело (система сил) находится в равновесии действием данной системы сил, то оно останется в равновесии и после отвердевания - все точки тела скрепить абсолютно жестко (пример-ножницы).

6 аксиома. Принцип освобождения от связей: всякое несвободное тело можно считать свободным, если отбросить связи, а их действие заменить реакцией этой связи.

Основные виды связей и их реакции.

Тело называется свободным, если его положение перемещения ничем не ограничено. Связи – тела,которые ограничивают перемещение тела в пространстве. Реакция связи - сила, с которой связь действует на выбранное тело. Реакции основных видов связей: 1. Гибкая невесомая нить (веревка, трос, канат и т.д.). Реакция направлена всегда от тела по нити. 2. Невесомый стержень, имеющий на концах идеальные шарниры. Реакция направлена по прямой, соединяя концы стержня. 3. Идеальная гладкая поверхность.Реакция направлена перпендикулярно общей касательной к точке контакта. 4. Сферический шарнир.Реакция приложена в центре шарнира и имеет произвольную ориентацию в пространстве. При решении задач реакцию раскладывают по 3 составляющим – коорд. осям x,y,z. 5. Цилиндрический шарнир, подшипник. Реакция цилиндрического шарнира приложена к оси шарнира и имеет произвольное направление в плоскость, перпендикулярной оси шарнира. При решении задач реакцию раскладывают на 2 составляющие по осям: x,y. 6. Подпятник. Реакция произвольно ориентирована в пространстве, задается 3 составляющими по осям x,y,z. 7.Шарнирно – неподвижная опора Реакция – как и у цилиндрического шарнира. 8. Шарнирно – подвижная опора.Реакция направлена перпендикулярно опорной плоскости.

Геометрический способ сложения сходящихся сил. Силовой многоугольник.

Сходящаяся система сил – система сил, линии действия кот пересекаются в одной точке.

Учитывая, что силы являются скользящими векторами, для сходящейся системы сил, все силы можно перенести по их линиям действия так, чтобы они были приложены в одной точке.

Геометрический способ определения равнодействующей сходящейся системы сил.

_{, , .} Равнодействующая сходящейся системы сил равна их геометрической сумме и приложена в точке пересечения линий действия. Ломаная линия ОАВСД – называется силовым многоугольником. Равнодействующая сходящейся системы сил приложена в точке их пересечения и является стороной, замыкающей силовой многоугольник.

Условие равновесия сходящихся сил в геометрической форме.

Сходящаяся система сил – система сил, линии действия кот пересекаются в одной точке.

Учитывая, что силы являются скользящими векторами, для сходящейся системы сил все силы можно перенести по их линиям действия так, чтобы они были приложены в одной точке.

- сходящаяся система сил

Условие равновесия системы сходящихся сил: система сходящихся сил является уравновешенной, если геометрическая сумма всех сил равна нулю.

Геометрическое условие равновесия:

для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнутым.

Аналитический способ сложения сходящихся сил. Проекции силы на оси координат.

Сходящаяся система сил – система сил, линии действия кот пересекаются в одной точке.

Учитывая, что силы являются скользящими векторами, для сходящейся системы сил все силы можно перенести по их линиям действия так, чтобы они были приложены в одной точке.

Аналитический способ:

_{, , , ,}

_{, , ,}

Приведенные выше формулы позволяют через проекции исходных сил на оси координат аналитически определить равнодействующую сходящейся системы сил.

Условия равновесия сходящихся сил в аналитической форме.

Сходящаяся система сил – система сил, линии действия кот пересекаются в одной точке.

Учитывая, что силы являются скользящими векторами, для сходящейся системы сил все силы можно перенести по их линиям действия так, чтобы они были приложены в одной точке.

- сходящаяся система сил

Условие равновесия системы сходящихся сил: система сходящихся сил является уравновешенной, если геометрическая сумма всех сил равна нулю.

Аналитическое условие равновесия:

_,

- уравнение равновесия пространств. с.с.с.

Для равновесия тела под действием сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на 3 координатных оси была равна нулю. Если сходящаяся система сил является плоской, то она имеет 2 уравнения равновесия.

Теорема о равновесии трех непараллельных сил(правило 3-х сил)

Если тело находится в равновесии действием 3-х сил, из которых 2 – сходящиеся, то линия действия 3-ей силы проходит через точку пересечения первых двух.

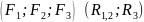
Силы - сходящиеся силы, следовательно их можно заменить одной силой , теперь на тело действуют две силы . По первой аксиоме статики эти силы будут уравновешенными, если они равны по модулю и направлены по одной прямой в противоположные стороны, следовательно лилия действия F₃ проходит через точку пересечения двух сил F₁ и F₂.

Момент силы относительно точки.

– момент силы F относительно точки O.

h – плечо силы относительно точки O/

Плечо силы – перпендикуляр, опущенный из точки на линию действия силы.

Определение 1.

Моментом силы относительно точки называется вектор, равный по модулю произведению модуля момента силы на плечо силы относительно этой точки и направленный перпендикулярно плоскости, в кот лежат эта сила и точка, в ту сторону, откуда видно, что сила вращает плоскость вокруг точки против часовой стрелки.

Вывод: модуль момента силы относительно точки равен удвоенной площади треугольника, основанием кот является сила, а точка находится в вершине треугольника.

Определение 2.

Моментом силы относительно точки называется вектор, равный векторному произведению радиус – вектора, проведенному из данной точки в точку приложения силы, на вектор силы.

Вывод: оба определения соответствуют одному вектору.

Момент силы относительно точки в плоском случае.

В плоском случае момент силы относительно точки называется скалярная величина равная произведению модуля силы на плечо, относительно данной точки. При этом момент имеет знак «+», если сила стремится повернуть плоскость против часовой стрелки, в противном случае знак «-».

Момент силы относительно точки равен 0, если линия действия силы проходит через эту точку.

1. Сложение параллельных сил.

- нахождение точки С.

2. Сложение антипараллельных сил.